标签:查找 空间 dia 实例 没有 ack com 指定 整数
问题描述:可以在多项式时间复杂度内求解;
举例:二分查找(O(logn))、快排(O(nlogn))
问题描述:可以在多项式时间复杂度内验证是否是可行解的问题;有指数时间复杂度的求解方法;这类问题可以用启发式算法求解,但只能得到一个相对的最优解;
举例:所有P问题(可以在多项式时间复杂度内把所有解求出来,然后用O(n)时间去查找解空间是否包含该解)、NPC问题(背包问题、旅行商问题)
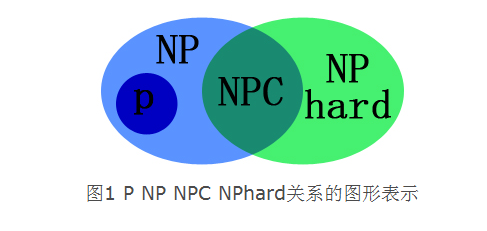
问题描述:最复杂的一类NP问题(NP包含P和NPC)。不能找到一个有效算法去求解(有效指在多项式时间复杂度内);有指数时间复杂度的求解方法(只有把解域里面的所有可能都穷举了之后才能得出答案);
举例:
背包问题(Knapsack problem)(回溯法、动态规划、贪心可解,不过时间复杂度都是指数级):01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2……Wn,与之相对应的价值为V1,V2……Vn。求出获得最大价值的方案。
旅行商问题(Traveling Saleman Problem,TSP)(回溯法、动态规划、启发式贪心可解,时间复杂度都是指数级),该问题是在寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到原点的最小路径成本。
哈密顿路径问题(Hamiltonian path problem)与哈密顿环路问题(Hamiltonian cycle problem)为旅行推销员问题的特殊案例。哈密顿图:由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。
欧拉回路(Fleury算法(深度优先遍历)可解,时间复杂度都是指数级)(从图的某一个顶点出发,图中每条边走且仅走一次,最后回到出发点;如果这样的回路存在,则称之为欧拉回路。)与欧拉路径(从图的某一个顶点出发,图中每条边走且仅走一次,最后到达某一个点;如果这样的路径存在,则称之为欧拉路径。)
无向图欧拉回路存在条件:所有顶点的度数均为偶数。
无向图欧拉路径存在条件:至多有两个顶点的度数为奇数,其他顶点的度数均为偶数。
有向图欧拉回路存在条件:所有顶点的入度和出度相等。
有向图欧拉路径存在条件:至多有两个顶点的入度和出度绝对值差1(若有两个这样的顶点,则必须其中一个出度大于入度,另一个入度大于出度),其他顶点的入度与出度相等。
解决办法:回溯法(带剪枝的DFS)、动态规划、贪心法、深度优先遍历(1、2、4都是以穷举为基础)
证明:要证明npc问题的思路就是: 1.先证明它至少是一个NP问题,2.再证明其中一个已知的NPC问题能约化到它。NPC问题是一个问题族,如果里面任意一个问题有了多项式的解,即找到一个算法,那么所有的问题都可以有多项式的解。
问题描述:比NPC还复杂的问题;所有的NPC问题都能规约到它,但它不一定是NP问题(NPC是NP-Hard问题);NP-Hard问题要比NPC问题的范围广,NP-Hard问题没有限定属于NP,即所有的NP问题都能约化到它,但是他不一定是一个NP问题。事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。
举例:所有NPC问题、TSP
售货员旅行问题 (traveling salesman problem),是最具有代表性的NP问题之一。假设一个推销员需要从香港出发,经过广州,北京,上海,…,等 n 个城市, 最后返回香港。 任意两个城市之间都有飞机直达,但票价不等。现在假设公司只给报销 C 块钱,问是否存在一个行程安排,使得他能遍历所有城市,而且总的路费小于 C?
规约/约化(简单的规约到复杂的,一般NP问题规约到最复杂的NP问题:NPC)
简单的说,问题A可以约化为问题B,就可以理解为:问题B的解就一定是问题A的解。
也可以理解为,“问题A可归约为问题B”,指问题B的答案可用于解决问题A。因此解决A不会难于解决B。
由此也可以知道的是问题B的时间复杂度一定会大于等于问题A。
《算法导论》上举了这么一个例子。比如说,现在有两个问题:求解一个一元一次方程和求解一个一元二次方程。那么我们说,前者可以规约为后者,意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题,那么我们能找到一个“规则”,按照这个规则把解一元一次方程程序的输入数据变一下,用在解一元二次方程的程序上,两个程序总能得到一样的结果。这个规则即是:两个方程的对应项系数不变,一元二次方程的二次项系数为0。
从规约的定义中我们看到,一个问题规约为另一个问题,时间复杂度增加了,问题的应用范围也增大了。通过对某些问题的不断规约,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。存在这样一个NP问题,所有的NP问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。这种问题的存在难以置信,并且更加不可思议的是,这种问题不只一个,它有很多个,它是一类问题。这一类问题就是传说中的NPC问题,也就是NP-完全问题。
确定/非确定算法
(1)确定性算法(Determinism): 设A是问题Π的一个解决算法,在算法的整个执行过程中,每一步都能得到一个确定的解,这样的算法就是确定性算法。
(2)非确定性算法(Nondeterminism):设A是求解问题Π的一个算法,它将问题分解成两部分,分别为猜测阶段和验证阶段,其中
猜测阶段:在这个阶段,对问题的输入实例产生一个任意字符串y,在算法的每一次运行时,串y的值可能不同,因此,猜测以一种非确定的形式工作。
验证阶段:在这个阶段,用一个确定性算法(有限时间内)验证:① 检查在猜测阶段产生的串y是否是合适的形式,如果不是,则算法停下来并得到no;② 如果串y是合适的形式,则验证它是否是问题的解,如果是,则算法停下来并得到yes,否则算法停下来并得到no。它是验证所猜测的解的正确性。
第一个NP-Complete问题在40年前被找到了,它就是著名的SAT问题。
所有的NPC问题:List_of_NP-complete_problems
组合最优化问题(combinatorial optimizationproblem)是一类在离散状态下求极值的问题。把某种离散对象按某个确定的约束条件进行安排,当已知合乎这种约束条件的特定安排存在时,寻求这种特定安排在某个优化准则下的极大解或极小解的间题。组合最优化的理论基础含线性规划、非线性规划、整数规划、动态规划、拟阵论和网络分析等。组合最优化技术提供了一个快速寻求极大解或极小解的方法。
标签:查找 空间 dia 实例 没有 ack com 指定 整数
原文地址:https://www.cnblogs.com/yuboyuan/p/14649686.html