leetcode 208 前缀树Trie

标签：逻辑   节点   创建   treenode   inf   不同   隐藏   turn   new   

前缀树又称字典树，每颗节点结构与一般树有一点不同。

一般树节点

struct TreeNode
{
valueType val;
vector<TreeNode*> next;//个数不固定，个数代表一个节点有多少个子节点
}

本题前缀树节点

struct TrieNode
{
bool isEnd;//记录这个节点是不是已经存进来的某个单词的最后一个字母
vector<TrieNode*> next;//个数为26个，分别代表26个字母。
}

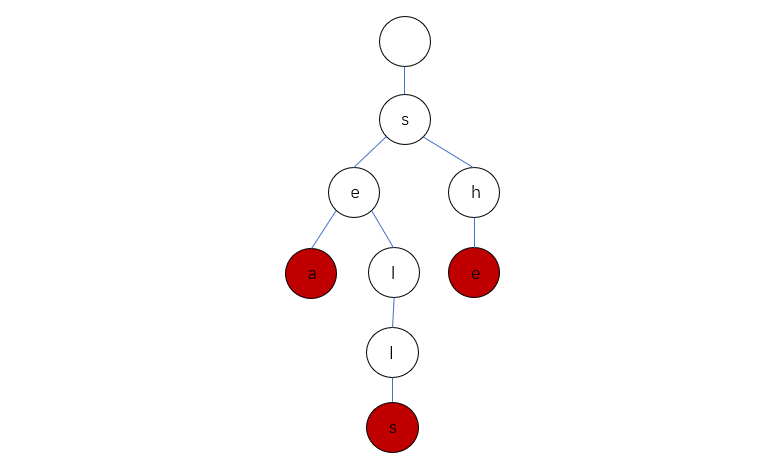
下图为前缀树的样子（隐藏了next中为nullptr的节点）

构造函数：Trie()

Trie():isEnd(false) ,next(26,nullptr)
{

}

注意，这里我用的vector，内存将由vector默认的allocater开辟，如果用的语言自带的原生数组(如：TrieNode* next[26]),需要自己手动开辟数组memset(next,0,sizeof(next))。

插入函数：void insert(String word)

分析：我们需要遍历这个单词的每一个字符c，并查看当前这个节点的next[c-‘a‘]是不是空，如果空，我们需要创建一个节点，并让next[c-‘a‘]指向它，如果不为空，就将node移动到它的next[c-‘a‘]继续查下去。如此下去，直至遍历word结束。结束时，将当前节点的isEnd置为true，表示这是一个单词的结尾。

void insert(string word) {
        Trie* node = this;
        for(char c : word)
        {
            if(node->next[c-‘a‘]==nullptr)
            {
                node->next[c-‘a‘] = new Trie();
            }
            node = node->next[c-‘a‘];
        }
        node->isEnd = true;
    }

查询函数：boolean search(String word)

分析：这里需要查询是否已经存有这个单词，我们只需遍历word，判断当前节点的next[c-‘a‘]是不是为空，空，就说明没有这个单词，非空，就节点下移，直至word扫描完毕。扫描完毕后，只能确定有这个前缀，所以还需要判断当前节点的isEnd标记，如果isEnd为true，表示确实有这个单词被存进来了，否则无。

bool search(string word) {
        Trie* node = this;
        for(char c : word)
        {
            if(node->next[c-‘a‘]==nullptr)
            {
                return false;
            }
            else
            {
                node = node->next[c - ‘a‘];
            }
        }
        return node->isEnd;
    }

查询前缀函数：boolean startsWith(String prefix)

分析：这个和前面的查询逻辑差不多，唯一的区别在于，不需要检查isEnd标记，只要遍历word都能找到对于的节点，就行。

bool startsWith(string prefix) {
        Trie* node = this;
        for(char c : prefix)
        {
            if(node->next[c - ‘a‘]==nullptr)
            {
                return false;
            }
            else
            {
                node = node ->next[c-‘a‘];
            }
        }
        return true;
    }

又学到一个新东西，前缀树
另外，写着写着，突然发现我写的是“节点”，看见有人是“结点”，我就查了下，发现都可以的哈！：）

leetcode 208 前缀树Trie

标签：逻辑   节点   创建   treenode   inf   不同   隐藏   turn   new   

原文地址：https://www.cnblogs.com/zzysmemory/p/14657011.html