码迷，mamicode.com
首页 > 其他好文 > 详细

「图论」第2章 最小生成树课堂过关

时间：2021-04-19 16:02:22      阅读：0      评论：0      收藏：0      [点我收藏+]

标签：没有   break   clu   遍历   思路   read   print   first   else   

目录

「图论」第2章 最小生成树课堂过关

A. 【例题1】繁忙都市

题目

技术图片

代码

prim

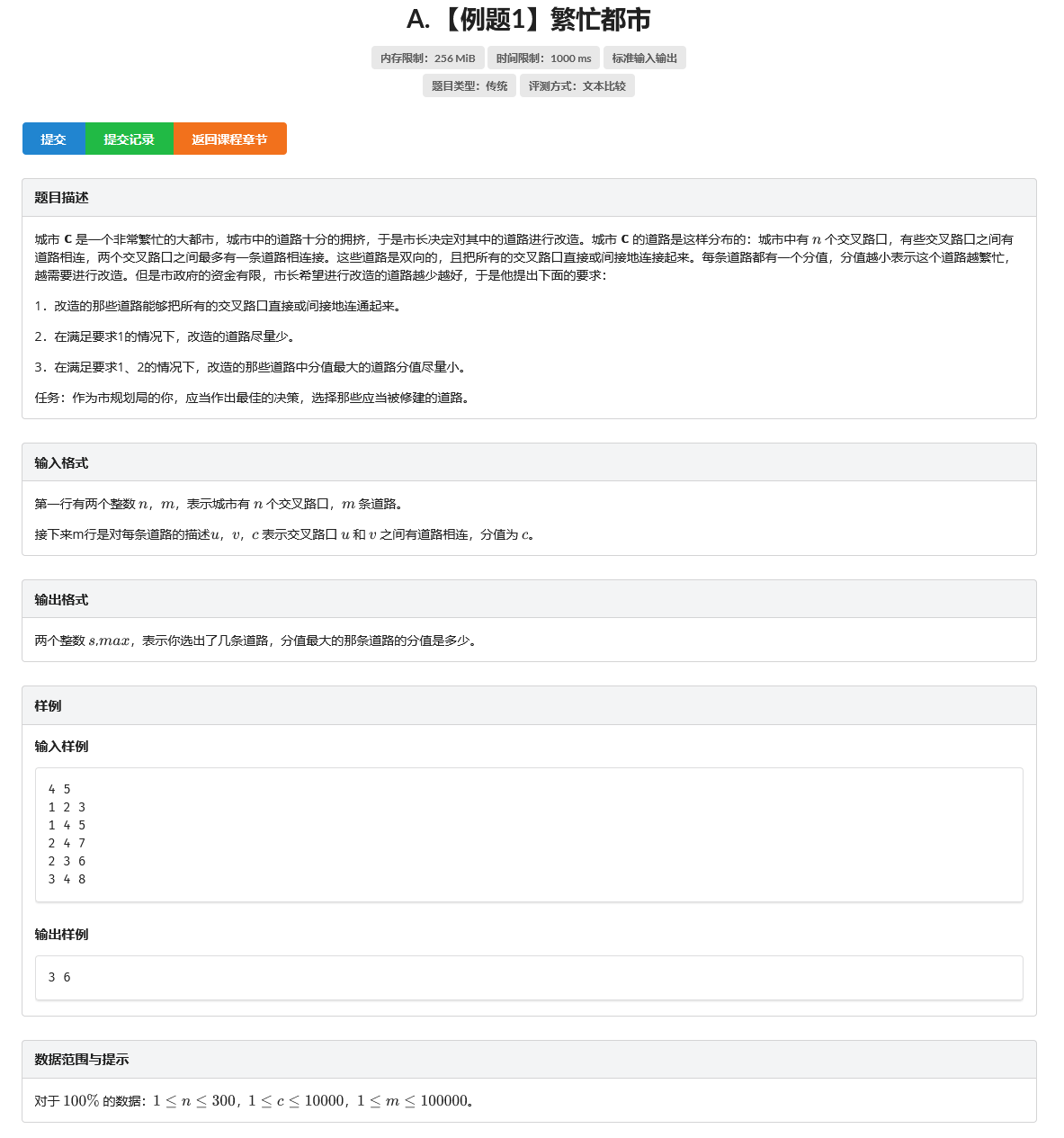
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 310
#define M 200010
struct Heap {
#define max_(_ , __) ((_) < (__) ? (_) : (__))
	int siz;
	int a[M * 2] , b[M * 2];
	bool ty;
	inline void swap_(int x , int y) {
		int tmp;
		tmp = a[y] , a[y] = a[x] , a[x] = tmp;
		tmp = b[y] , b[y] = b[x] , b[x] = tmp;
	}
	void clear() {
		siz = 0 , ty = 0;
		memset(a , 0 , sizeof(a));
		memset(b , 0 , sizeof(b));
	}
	inline void push(int dat , int dat2) {
		a[++siz] = dat;
		b[siz] = dat2;
		int p = siz;
		while(p > 1 && (!(a[p >> 1] < a[p]) ^ ty))
			swap_(p >> 1 , p) , p >>= 1;
	}
	inline void pop() {
		swap_(1 , siz);
		--siz;
		int p = 1 , tmp;
		while(p * 2 <= siz && (!(a[p] < a[tmp = ( p * 2 + 1 > siz ? p * 2 : (a[p * 2] < a[p * 2 + 1] ^ ty ? p * 2 : p * 2 + 1) ) ] ) ^ ty))
			swap_(tmp , p) , p = tmp;
	}
	inline int top_A() {
		return siz == 0 ? 0 : a[1];
	}
	inline int top_B() {
		return siz == 0 ? 0 : b[1];
	}
	inline bool empty() {
		return siz == 0;
	}
} h;

int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}
int nxt[M] , val[M] , to[M];
int head[N];
bool vis[N];
inline void addedge(int u , int v , int value) {
	static int cnt = 0;
	++cnt;
	val[cnt] = value , to[cnt] = v , nxt[cnt] = head[u] , head[u] = cnt;
}

int n , m;
int ans;
int main() {
	n = read() , m = read();
	for(int i = 1 ; i <= m ; i++) {
		int u , v , value;
		u = read() , v = read() , value = read();
		addedge(u , v , value);
		addedge(v , u , value);
	}

	for(int i = head[1] ; i ; i = nxt[i])
		h.push(val[i] , to[i]);
	vis[1] = true;
	for(int j = 2 ; j <= n ; j++) {
		while(vis[h.top_B()] && !h.empty())
			h.pop();
		if(h.empty())	break;
		int u = h.top_B();
		if(h.top_A() > ans)
			ans = h.top_A();
		h.pop();
		
		vis[u] = true;
		for(int i = head[u] ; i ; i = nxt[i]) {
			if(!vis[to[i]]) {
				h.push(val[i] , to[i]);
			}
		}
	}
	printf("%d %d" , n - 1 , ans);
	return 0;
}

Kruskal

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 310
#define M 100010
int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}
struct ednode{
	int u , v , val;
}ed[M];
bool cmp(ednode a , ednode b) {
	return a.val < b.val;
}
int fa[N];
int findroot(int x) {
	return fa[x] == x ? x : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
	fa[findroot(x)] = findroot(y);
}

int n , m;
int ans;
int main() {
	n = read() , m = read();
	for(int i = 1 ; i <= m ; i++)
		ed[i].u = read() , ed[i].v = read() , ed[i].val = read();

	sort(ed + 1 , ed + m + 1 , cmp);
	for(int i = 1 ; i <= n ; i++)
		fa[i] = i;
	for(int i = 1 ; i <= m ; i++) {
		if(findroot(ed[i].u) != findroot(ed[i].v)) {
			uni(ed[i].u , ed[i].v);
			if(ed[i].val > ans)
				ans = ed[i].val;
		}
	}
	printf("%d %d" , n - 1 , ans);
	return 0;
}

B. 【例题2】新的开始

题目

技术图片

思路

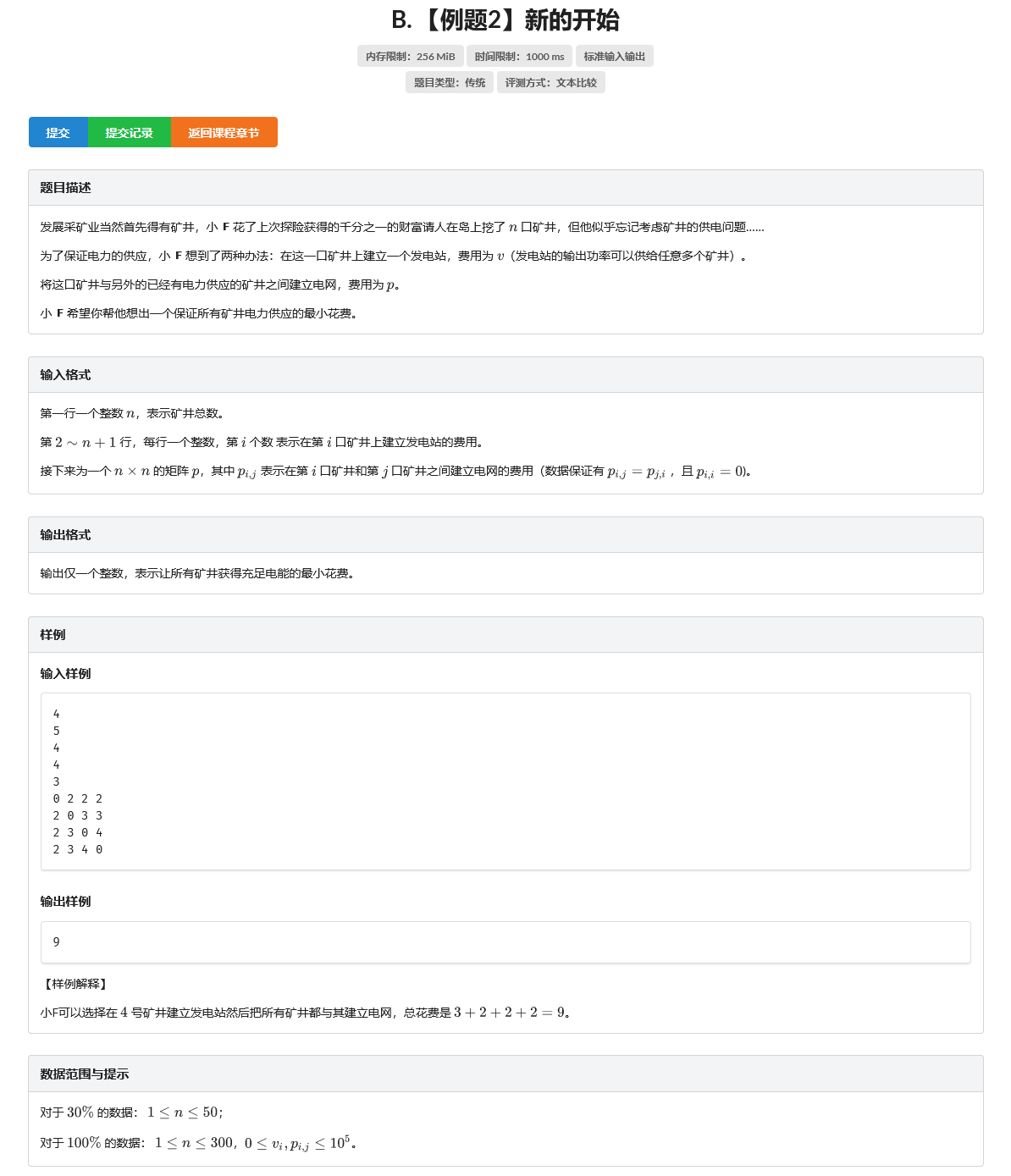
想象一个原点,它到\(i\)点的距离就是\(i\)建发电站的费用,其余连边不变,从那个原点开始跑一边最小生成树即可

代码

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define N 310
#define M N * N
struct Heap {
#define max_(_ , __) ((_) < (__) ? (_) : (__))
	int siz;
	int a[M * 2] , b[M * 2];
	bool ty;
	inline void swap_(int x , int y) {
		int tmp;
		tmp = a[y] , a[y] = a[x] , a[x] = tmp;
		tmp = b[y] , b[y] = b[x] , b[x] = tmp;
	}
	void clear() {
		siz = 0 , ty = 0;
		memset(a , 0 , sizeof(a));
		memset(b , 0 , sizeof(b));
	}
	inline void push(int dat , int dat2) {
		a[++siz] = dat;
		b[siz] = dat2;
		int p = siz;
		while(p > 1 && (!(a[p >> 1] < a[p]) ^ ty))
			swap_(p >> 1 , p) , p >>= 1;
	}
	inline void pop() {
		swap_(1 , siz);
		--siz;
		int p = 1 , tmp;
		while(p * 2 <= siz && (!(a[p] < a[tmp = ( p * 2 + 1 > siz ? p * 2 : (a[p * 2] < a[p * 2 + 1] ^ ty ? p * 2 : p * 2 + 1) ) ] ) ^ ty))
			swap_(tmp , p) , p = tmp;
	}
	inline int top_A() {
		return siz == 0 ? 0 : a[1];
	}
	inline int top_B() {
		return siz == 0 ? 0 : b[1];
	}
	inline bool empty() {
		return siz == 0;
	}
} h;

int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}
int n , m;
int ans;
int map[N][N];
bool vis[N];
int main() {
	n = read();
	for(int i = 1 ; i <= n ; i++)
		h.push(read() , i);
	for(int i = 1 ; i <= n ; i++)
		for(int j = 1 ; j <= n ; j++) {
			map[i][j] = read();
		}

	for(int j = 1 ; j <= n ; j++) {
		while(vis[h.top_B()] && !h.empty())
			h.pop();
		if(h.empty())	break;
		int u = h.top_B();
		ans += h.top_A();
		h.pop();

		vis[u] = true;
		for(int i = 1 ; i <= n ; i++) {
			if(!vis[i])
				h.push(map[i][u] , i);
		}
	}
	printf("%d" , ans);
	return 0;
}

C. 【例题3】公路建设

题目

技术图片

思路

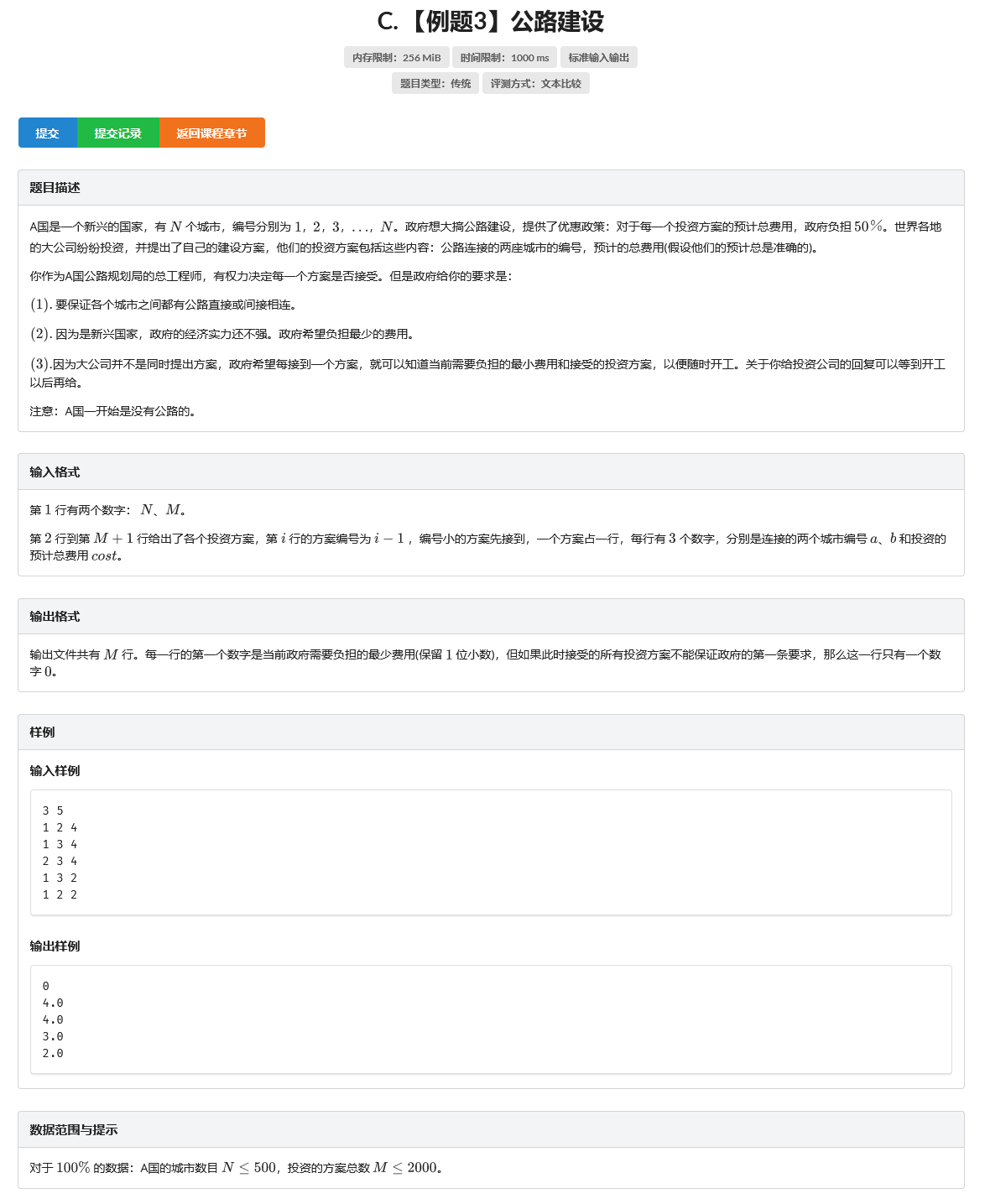
题目的意思是给定\(m\)条边,依次加入一开始没有边的图\(G\)中,若当前加入的边不能使\(G\)强连通,输出"0",否则,输出图\(G\)的最小生成树

我们把边依次加入一条链中,按插入排序的思想维护链的有序性,跑一次Kruskal就可以求出当前的最小生成树

时间复杂度\(O(n\cdot m)\)

代码

#include <iostream>
#include <cstdio>
#define N 510
#define M 2010
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}
struct ednode {
	int x , y , val , nxt;
}ed[M];
int head = 1;
void insert(int x , int y , int val) {
	static int cnt = 0;
	++cnt;
	ed[cnt].x = x , ed[cnt].y = y , ed[cnt].val = val;
	if(cnt == 1)	return;
	int p = head;
	if(val < ed[p].val) {
		ed[cnt].nxt = head , head = cnt;
		return;
	}
	for( ; ed[p].nxt != 0 ; p = ed[p].nxt)
		if(ed[p].val <= val && val <= ed[ed[p].nxt].val) {
			ed[cnt].nxt = ed[p].nxt , ed[p].nxt = cnt;
			return;
		}
	ed[p].nxt = cnt;
	ed[cnt].nxt = 0;
	return;
}

int n , m;
int fa[N];
int findroot(int x) {
	return fa[x] == x ? x : (fa[x] = findroot(fa[x]));
}
void uni(int x , int y) {
	fa[findroot(x)] = findroot(y);
}


int main() {
	n = read() , m = read();
	for(int i = 1 ; i <= m ; i++) {
		int u = read() , v = read() , val = read();
		insert(u , v , val);
		
		for(int j = 1 ; j <= n ; j++)
			fa[j] = j;
			
		int ans = 0;
		for(int j = head ; j ; j = ed[j].nxt)
			if(findroot(ed[j].x) != findroot(ed[j].y)) {
				uni(ed[j].x , ed[j].y);
				ans += ed[j].val;
			}
		int ty = true;
		int sta = findroot(1);
		for(int i = 1 ; i <= n ; i++)
			if(findroot(i) != sta) {
				ty = false;
				break;
			}
		if(!ty)
			puts("0");
		else
			printf("%.1f\n" , ans * 0.5);
	}
	
	return 0;
}

D. 【例题4】构造完全图

题目

技术图片

思路

50分

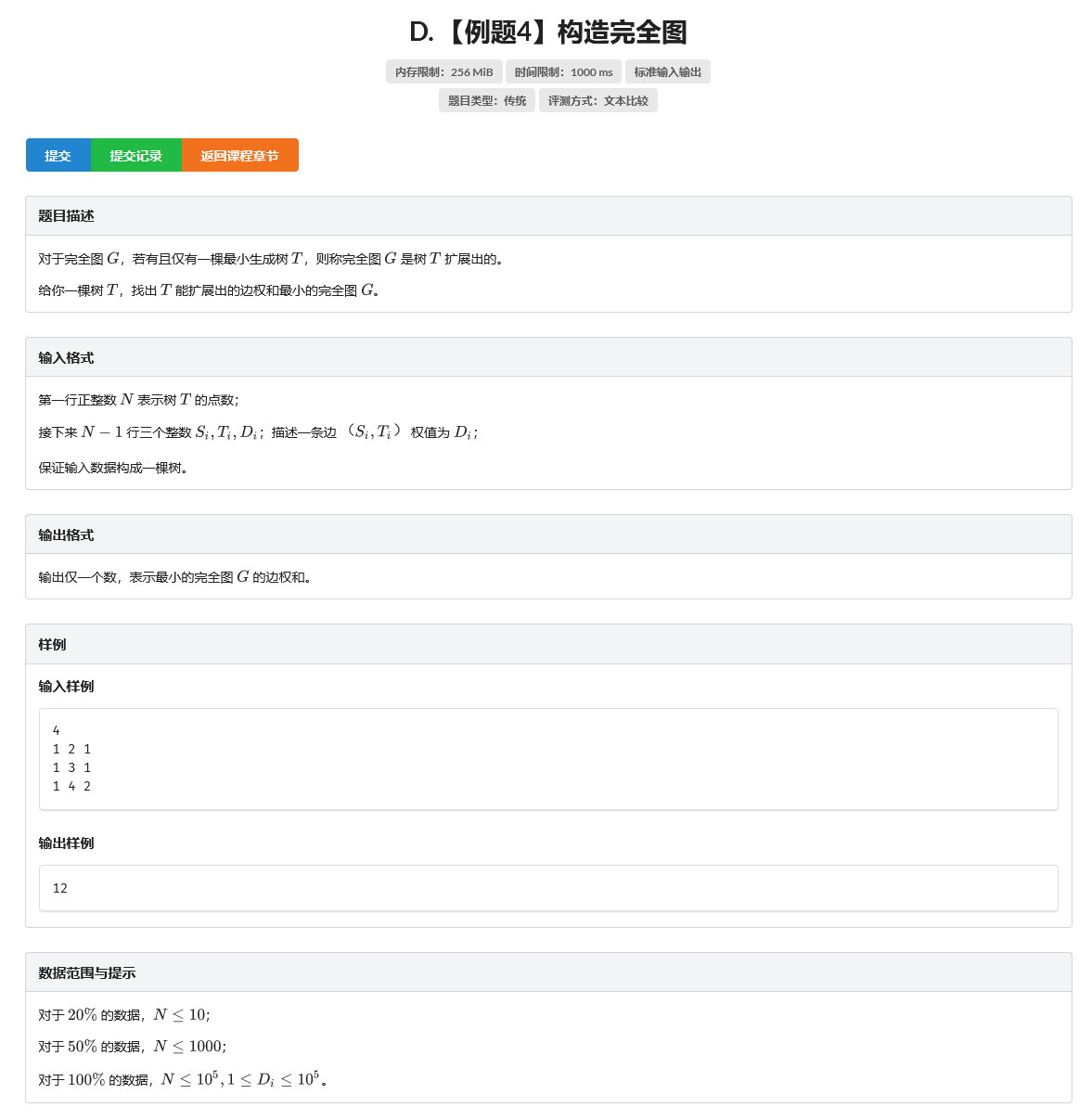
有一个贪心:如果\(u\)到\(v\)路径上最大边权为\(val\),则\(u\),\(v\)之间连一条边权小于等于\(val\)的边,原最小生成树会改变,否则不会改变.具体的证明可以从边权及边的数量出发,这里不再赘述

因此,直接枚举每个点,各跑一边深搜遍历整棵树即可,时间复杂度\(O(n^2)\)

100分

从数据规模可以看到,\(n\)去到\(10^5\),即边的数量可以达到\(10^{10}\),一条一条算肯定是不行的.

考虑对于最小生成树的每一条边\(ed_i\),它连接两个连通块\(T_1\),\(T_2\),大小为\(val\),它一定是连接\(T_1\),\(T_2\)所有边中最小的,设\(T_1\)中有\(siz_1\)个节点,\(T_2\)中有\(siz_2\)个节点,则除了\(ed_i\),一共有\(siz_1 \cdot siz_2-1\)条,每条(除\(ed_i\)外)的最小权值为\(val+1\)

更具体地,代码解释吧

代码

50分

#include <iostream>
#include <cstdio>
#define ll long long
#define N 100010
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}

struct ednode {
	int to , val , nxt;
}ed[N * 2];
int head[N];
inline void addedge(int x , int y , int v) {
	static int cnt = 0;
	++cnt;
	ed[cnt].to = y , ed[cnt].val = v , ed[cnt].nxt = head[x] , head[x] = cnt;
	return;
}

int n;
ll ans;

void dfs(int x , int maxv , int fa , int dep) {
	if(dep > 1)			ans += maxv + 1;
	for(int i = head[x] ; i ; i = ed[i].nxt) {
		if(ed[i].to == fa)	continue;
		dfs(ed[i].to , maxv > ed[i].val ? maxv : ed[i].val , x , dep + 1);
	}
}

int main() {
	n = read();
	for(int i = 1 ; i < n ; i++) {
		int u = read() , v = read() , val;
		ans += (val = read()) * 2;
		addedge(u , v , val);
		addedge(v , u , val);
	}
	for(int i = 1 ; i <= n ; i++) {
		dfs(i , -1 , i , 0);
	}
	cout << ans / 2;
	return 0;
}

100分

#include <iostream>
#include <cstdio>
#include <algorithm>
#define N 100010
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	while(c < ‘0‘ || c > ‘9‘)
		c = getchar();
	while(c >= ‘0‘ && c <= ‘9‘)
		re = (re << 1) + (re << 3) + c - ‘0‘,
		c = getchar();
	return re;
}

struct ednode{
	int u , v , val;
}ed[N * 2];
bool cmp(ednode a , ednode b) {
	return a.val < b.val;
}

int fa[N] , siz[N];
int findroot(int x) {
	return x == fa[x] ? x : (fa[x] = findroot(fa[x]));
}
int n;
long long ans;
int main() {
	n = read();
	for(int i = 1 ; i < n ; i++)
		ed[i].u = read() , ed[i].v = read() , ans += (ed[i].val = read());
		
	sort(ed + 1 , ed + n , cmp);
	for(int i = 1 ; i <= n ; i++)
		fa[i] = i , siz[i] = 1;
	
	for(int i = 1 ; i < n ; i++) {
		int u = findroot(ed[i].u) , v = findroot(ed[i].v);
		if(u != v) {
			ans += (long long)(siz[u] * siz[v] - 1) * (ed[i].val + 1);
			fa[u] = v;
			siz[v] += siz[u];
		}
	}
	cout << ans;
	return 0;
}

随机数据生成

#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
	return (long long) rand() * rand() % (r - l + 1) + l; 
}
pair <int,int> ed[1000010];
int dict[1000010];//用于打乱结点编号,有些有向图不适用
int main() {
	unsigned seed;
	cin >> seed;
	seed *= time(0);
	srand(seed);//外界输入种子
	
	int n = random(1e4 , 5);
	for(int i = 1 ; i <= n ; i++)
		dict[i] = i;
	random_shuffle(dict + 1 , dict + n + 1);
	for(int i = 1 ; i < n ; i++) {
		ed[i].first = random(i);
		ed[i].second = i + 1;
	}
	printf("%d\n" , n);
	
	random_shuffle(ed + 1 , ed + n);//随机打乱
	for(int i = 1 ;i < n ; i++)
		printf("%d %d %d\n" , dict[ed[i].first] , dict[ed[i].second] , random(1e5));
	
	return 0;
}

「图论」第2章 最小生成树课堂过关

标签：没有   break   clu   遍历   思路   read   print   first   else   

原文地址：https://www.cnblogs.com/dream1024/p/14670990.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！