标签:ati public 直接 sort strong date for tree info
平衡因子:左子树和右子树的高度差;
AVL树仍是二叉查找树,对任意结点其
class ANode {
int value;
ANode left;
ANode right;
int height;
?
public ANode(int value) {
this.value = value;
this.height = 1;//初始高度
}
?
//计算平衡因子
public int getBF() {
return left.height() - right.height();
}
?
//返回节点的高度
public int height() {
return height;
}
?
//更新节点高度
public void updateHeight() {
this.height = Math.max(left.height, right.height) + 1;
}
?
}
public class AvlTree {
ANode root;
?
//左旋
public void leftRotation(ANode root) {
ANode temp = root.right;
root.right = temp.left;
temp.left = root;
root.updateHeight();
temp.updateHeight();
root = temp;
}
?
//右旋
public void rightRotation(ANode root) {
ANode temp = root.left;
root.left = temp.right;
temp.right = root;
root.updateHeight();
temp.updateHeight();
root = temp;
}
?
//插入节点:每次插入同时调整树和更新节点高度
public void insert(ANode root, int value) {
if (root == null) {
root = new ANode(value);
return;
}
if (root.value < value) {
insert(root.right, value);
root.updateHeight();
if (root.getBF() == -2) {
if (root.right.getBF() == -1) {
leftRotation(root);
} else if (root.right.getBF() == 1) {
rightRotation(root.right);
leftRotation(root);
}
}
} else {
insert(root.left, value);
root.updateHeight();
if (root.getBF() == 2) {
if (root.left.getBF() == 1) {
rightRotation(root);
} else if (root.left.getBF() == -1) {
leftRotation(root.left);
rightRotation(root);
}
}
}
}
}
左旋
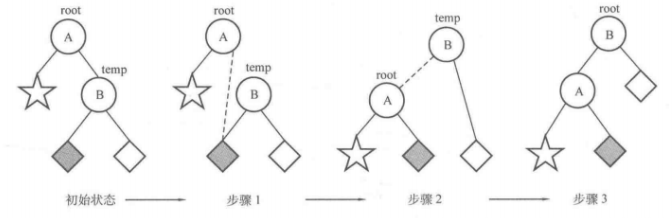
右旋
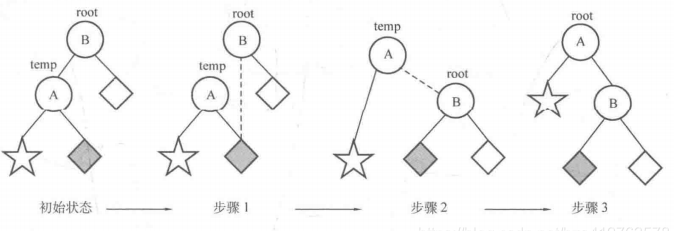
LR型
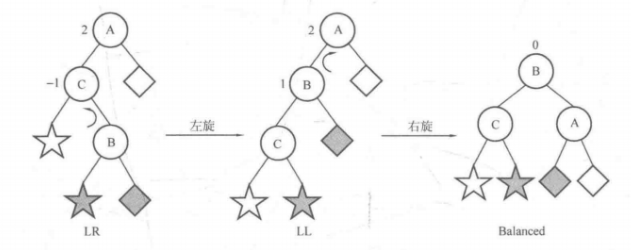
RL型
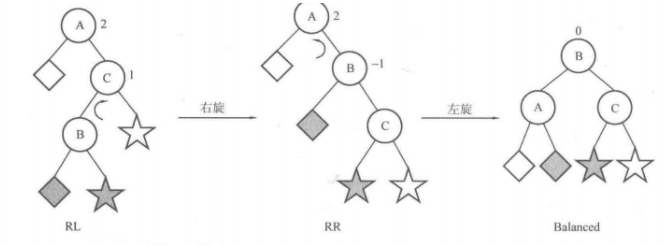
| 类型 | 判定条件 | 调整 |
|---|---|---|
| LL | BF(root) = 2 && BF(root.left) = 1 | root右旋 |
| LR | BF(root) = 2 && BF(root.left) = -1 | root.left左旋,再root右旋 |
| RR | BF(root) = -2 && BF(root.right) = -1 | root左旋 |
| RL | BF(root) = -2 && BF(root.right) = 1 | root.right右旋,再root左旋 |
*(图片来自《算法笔记》)
暂时放着
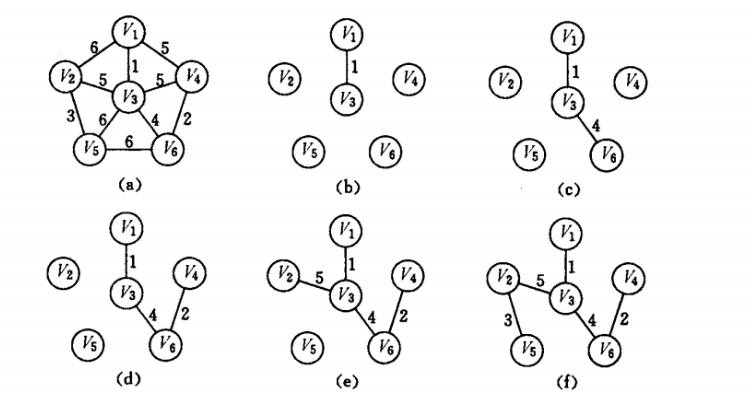
无向连通图,选取:
全部n个顶点,n-1条边,形成树,且边权之和最小
结果不一定唯一,但权值和唯一
每次基于点选取最优边加入
class MinTree {
//建图
public void create(MGraph mg, int verxs, char[] data, int[][] weight) {
int i, j;
for (i = 0; i < verxs; i++) {
mg.data[i] = data[i];
for (j = 0; j < verxs; j++) {
mg.weight[i][j] = weight[i][j];
}
}
}
//显示图
//prim v为起点
public void prim(MGraph graph,int v){
//标记数组
int[] visited = new int[graph.verxs];
?
visited[v] = 1;//当前节点已访问
int h1 = -1,h2 = -1;
int minweight = Integer.MAX_VALUE;
?
for(int k = 1;k < graph.verxs;k++){//最终选n-1条边
for(int i = 0;i < graph.verxs;i++){//i 为已访问的部分
for(int j = 0;j < graph.verxs;j++){//j 为未访问部分
//找出已选部分连向未选部分的最小权边
if(visited[i]==1 && visited[j] == 0 && graph.weight[i][j] < minweight){
minweight = graph.weight[i][j];
h1=i;
h2=j;
}
}
}
//h1->h2 为所选边
//记录或处理
visited[h2] = 1;
}
}
}
class MGraph {
int verxs;
char[] data;
int[][] weight;
?
public MGraph(int verxs) {
this.verxs = verxs;
data = new char[verxs];
weight = new int[verxs][verxs];
}
}
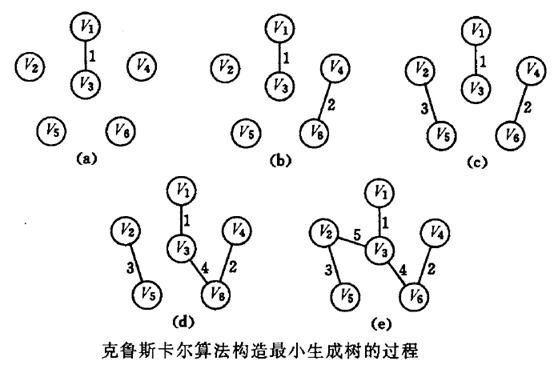
每次直接按边选最小
public class Kruskal {
?
private int edge;//边数
private char[] vertexs;//顶点数组
private int[][] matrix;//邻接矩阵
//不能连通的值
private static final int INF = Integer.MAX_VALUE;
?
private int getPosition(char ch) {
for (int i = 0; i < vertexs.length; i++) {
if (vertexs[i] == ch) {
return i;
}
}
return -1;
}
//并查集ends记录i的终点
private int getEnd(int[] ends,int i){
while (ends[i] != 0){
i = ends[i];
}
return i;
}
?
//获取边
private Edge[] getEdges(){
int index = 0;
Edge[] edges = new Edge[edge];
for (int i = 0; i < vertexs.length; i++) {
for (int j = i+1; j < vertexs.length; j++) {
if(matrix[i][j] != INF){
edges[index++] = new Edge(vertexs[i],vertexs[j],matrix[i][j]);
}
}
}
return edges;
}
?
public Kruskal(char[] vertexs, int[][] matrix) {
int len = vertexs.length;
this.vertexs = new char[len];
for (int i = 0; i < len; i++) {
this.vertexs[i] = vertexs[i];
}
int sum = 0;
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
this.matrix[i][j] = matrix[i][j];
if (matrix[