标签:namespace 二进制 定义 bsp its 图解 压缩 const ima
------------恢复内容开始------------
题意:给一个长度为n的序列ai,每次从ai中挑出一个数字走ai步(不能重复用),对应坐标也增加ai.问你有多少种方案走完ai这个序列,且中途没有坐标停留在给定的
数字k上(k是一个或者是两个)。n=24
思路:n=24,非常微妙的数字。首先n!的算法的上界是11,所以全排列是不能用的。而2的n次方算法上界是25左右,勉勉强强。所以我们使用状态压缩来解决这个问题。
定义dp[S]为S状态下的合法方案数.
转移方程就是 S去掉每个对应的1的方案求和 用图解表示比较方便.
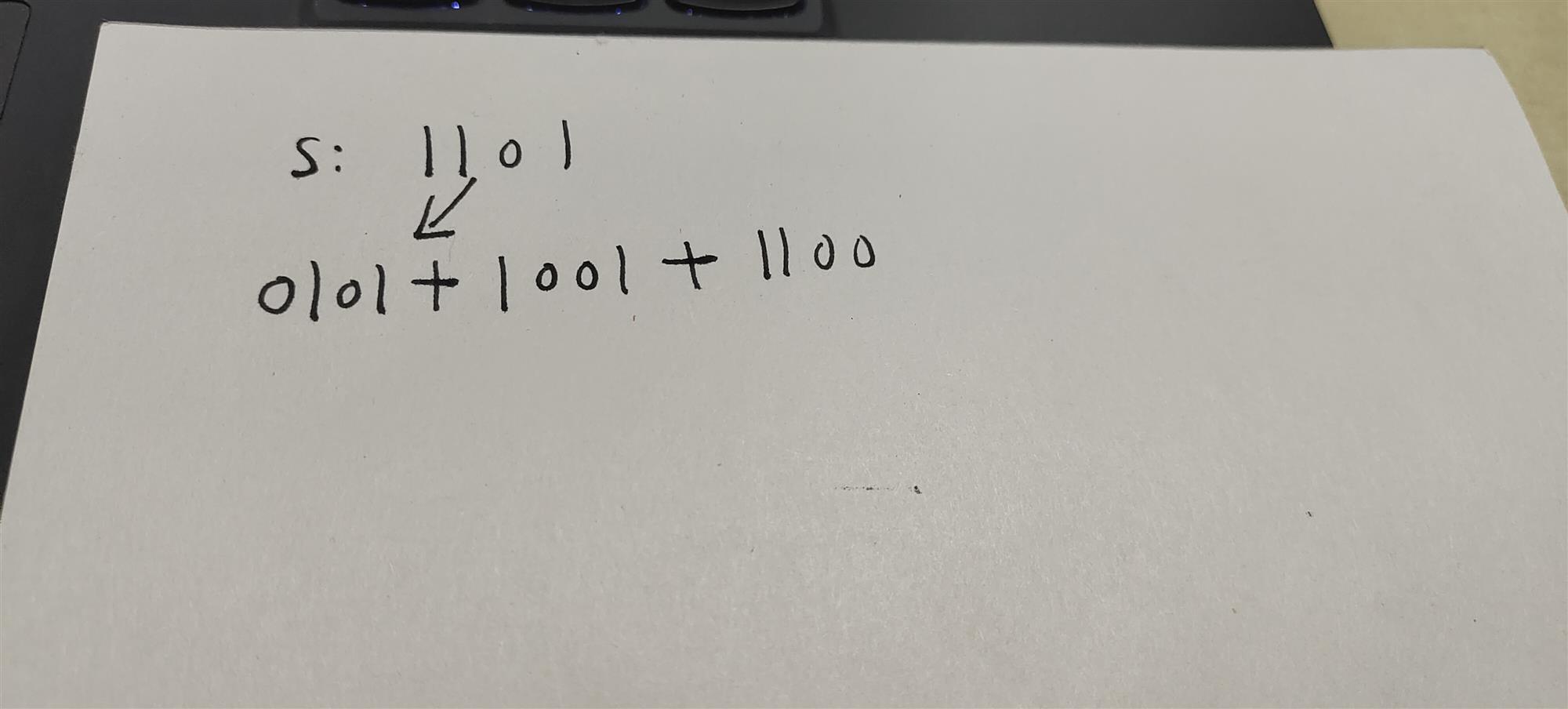
大概就是这么个意思,到代码实现上 就是每次减去对应的lowbit了.lowbit学过树状数组都知道,表示一个数二进制的最后一个1.然后操作一下就可以了。对于sum数组的求和,不用在转移前求好,在转移时顺便求了就好了。
代码:
#include<bits/stdc++.h> using namespace std; const int mod = 1e9+7; const int maxn = (1<<24)+5; int dp[maxn];long long sum[maxn]; int a[30];int _k[2]; int lowbit(int x){ return x&-x; } int main(){ int n,k,k1,k2;cin>>n; for(int i=0;i<n;i++) scanf("%d",&a[i]); cin>>k; for(int i=0;i<k;i++) cin>>_k[i]; for(int i=0;i<n;i++) { sum[1<<i]=a[i]; } dp[0]=1; for(int S=0;S<(1<<n);S++){ sum[S]=sum[S& ~lowbit(S)]+sum[lowbit(S)]; if(sum[S]==_k[0]||sum[S]==_k[1]) continue; for(int i=S;i!=0;i-=lowbit(i)){ dp[S]=(dp[S]+dp[S& ~lowbit(i)])%mod; } } cout<<dp[(1<<n)-1]; return 0;}
CF_327E Axis Walking 状态压缩中lowbit的运用
标签:namespace 二进制 定义 bsp its 图解 压缩 const ima
原文地址:https://www.cnblogs.com/minato-yukina/p/14686414.html