标签:sort 个人 code size 处理 时间 复杂度 大小 调用
Insertion Sort(插入排序)
思路:for 循环遍历数组中的每一个数
用while将每次遍历到的数于左侧的数进行对比,将小的排到左边
void InsertionSort(int*A, int n){ int key,i=0,p; for(p=0;p<n;p++){ key=A[p]; i=p-1; while(i>=0 && A[i]>key){ A[i+1]=A[i]; i=i-1; } A[i+1]=key; } }
中规中矩的排序方法
时间复杂度:
Best-case Running time : O(n)(数组已经被排好序的情况)
Worst-case Running Time : O(n^2)
Average Running Time : O(n^2)
从时间复杂度来看,处理少量数据还可以。当数据量较为庞大时,速度就很慢了
Merge Sort
思路:利用递归将数组分成两个相同大小的部分,直至长度为1
然后利用merge函数分别对每个部分进行排序
最后重新放在一起
void Merge(long int*A,long int left,long int center,long int right){ long int i1=left,i2=center+1,i=0,j; long int B[100000]; long int length =sizeof(B)/sizeof(B[0]); //比较左右两侧的大小,然后将小的的放入数组B while (i1<=center && i2<=right) { if(A[i1]>A[i2]){ B[i++]=A[i2++]; }else{ B[i++]=A[i1++]; } } //将左侧或者右侧剩余的数以此放入数组B中 for(;i1<=center;i1++){ B[i++]=A[i1]; } for(;i2<=right;i2++){ B[i++]=A[i2]; } //将数组B中排好序的值赋给A //由于每调用一次函数,B数组都会重新创建,因此B从0开始,A从left开始 for(j=0,i=left;j<=right-left;j++,i++){ A[i]=B[j]; } } void MergerSort(long int*A,long int left,long int right){ long int center=0; if(left>=right){ return ; } center=(left+right)/2; //这种先进行第一个递归,直至最后,没进行一次就相当于建立一层平台,当进行完后再返回上一层,执行下一个语句 MergerSort(A,left,center); MergerSort(A,center+1,right); Merge(A,left,center,right); }
这个就是merge sort 的排序过程:
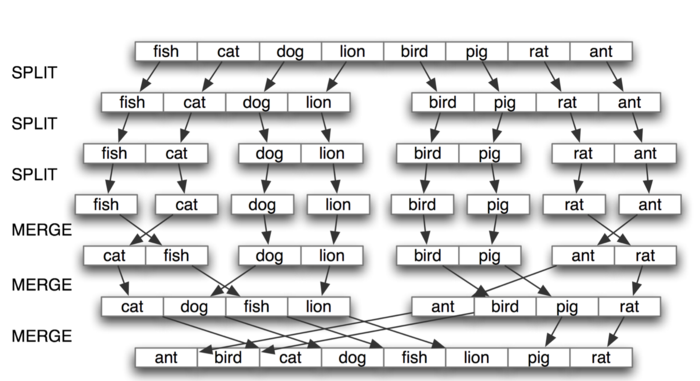
个人觉得递归部分的代码不是很好理解,其余部分都还可以
时间复杂度:
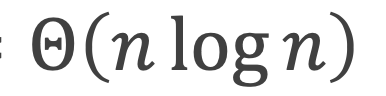
标签:sort 个人 code size 处理 时间 复杂度 大小 调用
原文地址:https://www.cnblogs.com/wekong/p/14699996.html