标签:不同 加法 parameter inline 实用 alt 常见 间隔 区间
B样条曲线
定义
B样条的形式与Bezier曲线的定义方式相同,是B-样条基函数的线性组合。
给定n+1个控制点\(P_i(i=0,1,...,n)\)和一个节点向量\(U=\{u_0,u_1,..., u_m\}\),且\(m=n+p+1\),依次连接这些控制点可以构成一个特征多边形,k+1阶(k次)B样条曲线的表达式为
\[p(u)=\sum_{i=0}^nP_iN_{i,k}(u)
\]
其中\(u_i\)称为节点(knots),\(u_0 <= u_1 <= u_2 <= ... <= u_m\), 半开区间\([u_i, u_i+1)\) 是第i个节点区间。。如果基函数的节点是允许存在重复的,如果\(u_i\)出现了k次(k>1),那么称其为k重节点。如果\(u_i\)仅出现一次,那么称其为简单节点。节点等间距(\(u_i+1 - u_i\)是一个常数,对\(0<=i<=m-1\)),节点向量或节点序列称为均匀的;否则它是非均匀的。
基函数
B样条的基函数由三个参数决定:阶数p,参数u,第i个基函数,Cox-de Boor递归定义如下:
\[N_{i, 0}(u) =\begin{cases}
1, \ if \ u_i \leq u < u_{i+1}\0, \ otherwise
\end{cases}
\N_{i, p}(u) = \frac{u - u_i}{u_{i+p}-u_i}N_{i,p-1}(u) + \frac{u_{i+p+1} - u}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}(u)
\]
B样条基函数\(N_{i,p}\)的作用范围是局部的,因此与Bezier曲线不同,移动控制点\(N_{i,p}\)对B样条的影响是局部的。其导数为
\[\frac{d}{du}N_{i,p}(u)=N‘_{i,p}(u)=\frac{p}{u_{i+p}-u_i}N_{i,p-1}-\frac{p}{u_{i+p+1}-u_{i+1}}N_{i+1,p-1}
\]
曲线形状
由控制点的位置(n+1),节点位置(m+1),和曲线的次数p决定。
- 开B-样条曲线:产生的曲线不会与控制折线的第一边和最后一边接触。
- clamped B-样条曲线:强制第一个节点和最后一个节点的重复度为p+1,那么产生的曲线就会分别与第一个控制点和最后一个控制点的第一边和最后一边相切,首尾点分别与首尾控制点相同。
- 闭B-样条曲线:通过重复某些节点和控制点,产生的曲线会是闭曲线。会产生闭环
拟合
给定已知点集\(\{F_0,F_1,…,F_t\}\)共\(t+1\)个点,求B样条曲线。其中要求必须经过所有点称为插值拟合,否则称为近似拟合,近似拟合必经\(F_0\)和\(F_t\),其他点可以不经过。下面是点集相同时两种拟合对应的曲线。
近似拟合
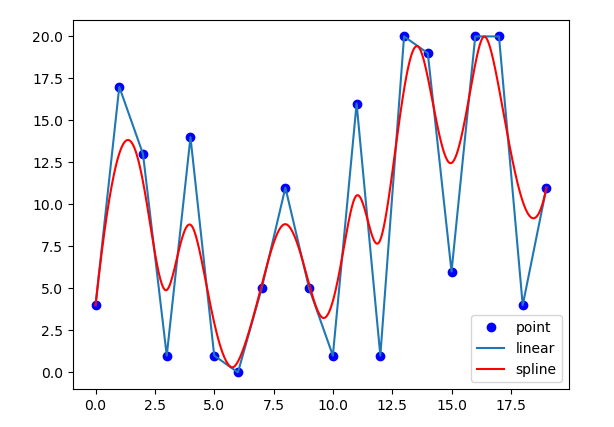
插值拟合
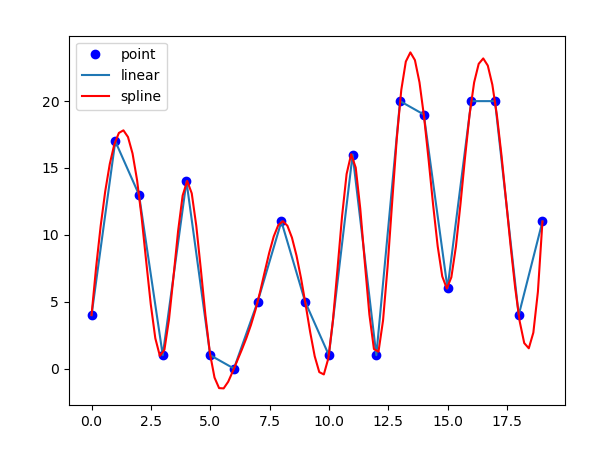
插值拟合
由已知条件可知
\[\left[\begin{matrix}
N_0(u_0) & \cdots & N_i(u_0) & \cdots & N_p(u_0) \N_0(u_1) & \cdots & N_i(u_1) & \cdots & N_p(u_1) \\vdots & & \vdots & & \vdots\N_0(u_t) & \cdots & N_i(u_t) & \cdots & N_p(u_t) \\end{matrix}
\right]
\left[
\begin{matrix}
P_0 \\vdots \P_i \\vdots\P_n
\end{matrix}
\right]
=
\left[
\begin{matrix}
F_0 \F_1 \\vdots\F_t
\end{matrix}
\right]
\tag 1
\]
1. 参数化
给\(F_i\)确定\(u_i\)的过程,称之为参数化(Parameterization)。常见的参数化方法有三种:弦长累加法(chord length),向心参数法(也称平方根法),统一节点法。其中前两种最为常用。
- 弦长累加法:指的是,当前型值点\(Fi\)的参数,等于之前所有型值点长度的累加\(∑_{j=1}^i|F_{j?1}F_j|\)。这种方法是“Arc-Length”参数法的一种近似,选用弦长代替弧长,因此具有比较好的效果。
- 向心参数法:这个方法由波音公司的技术人员提出。指的是当前型值点的参数是由之前所有型值点长度的平方根累加的值\(∑_{j=1}^i\sqrt{|F_{j?1}F_j|}\),通常情况下,这个方法的效果要好于弦长累加法,尤其是在节点分布不均匀的情况下。
- 统一节点法:顾名思义,每个节点的间隔都是相等的。这种方法不怎么在实践中获得应用。
2.阶次
B-Spline的三个要素是节点(序列)、阶次、控制点。阶次由我们确定。样条曲线的性质是n阶B样条在节点处有n-1阶连续性。这里选择p=3,进而得出曲线的节点序列为(clamped B样条曲线):
\[\{0,0,0,0,u_1,\cdots,u_i,\cdots,u_t,u_t,u_t,u_t\}
\]
这样就确定了每个节点对应的基函数的值,从而N已知,F已知,但前面方程\((1)\)是一个欠定方程,节点数为t+7个,对应控制点为m-p-1=t+3个,没有唯一解,所以至少还需要与t有关的两个边界条件。
3.边界条件
一般来说,最常用或者说最实用的边界条件通常是两条:曲线在首尾点的切矢量。常用的切矢量推导算法是”Bessel Tangents“。再结合B样条的求导,可以知道首尾处的导数为
\[\begin{cases}
C‘(0)=\frac{p}{u_{p+1} - u_1}(P_1 - P_0); \C‘(u_t)=\frac{p}{u_{p+n} - u_n}(P_n - P_{n-1}); (n = t + 2)
\end{cases}
\]
即
\[\left[
\begin{matrix}
-1 & 1 & 0 & \cdots & 0 \0 & \cdots & 0 & -1 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
P_0 \\vdots \P_i \\vdots\P_n
\end{matrix}
\right]
=
\left[
\begin{matrix}
C‘(0)\frac{u_{p+1} - u_1}{p} \C‘(u_t)\frac{u_{p+n} - u_n}{p}
\end{matrix}
\right]
\tag2
\]
联合(1)(2)式,即可求解出所有的控制点。
B样条系列(1)
标签:不同 加法 parameter inline 实用 alt 常见 间隔 区间
原文地址:https://www.cnblogs.com/proboxdu/p/bspline_1.html

