标签：中序   child   长度   线索二叉树   总结   data   算法   哈夫曼树   return   

树与二叉树的思维导图：

重要概念：

• 树是由n(n>=1)个结点（或元素）组成的有限集合

• 二叉树是一个有限的结点集合，这个集合或者为空，或者由一个根结点和两棵互不相交的称为左子树和右子树的二叉树组成

二叉树的遍历：

• 先序遍历：
  (1)访问根结点；
  (2)先序遍历左子树；
  (3)先序遍历右子树；
  代码如下：

   void PreOrder(BTNode *b)
   {  if(b!=NULL)
      {  printf("%c",b->data);//访问根节点
         PreOrder(b->lchild);//先序遍历左子树
         PreOrder(b->rchild);//先序遍历右子树

• 中序遍历：
  (1)中序遍历左子树；
  (2)访问根节点；
  (3)中序遍历右子树；

   void InOrder(BTNode *b)
   {  if(b!=NULL)
      {  InOrder(b->lchild);
         printf("%c",b->data);
         InOrder(b->rchild);

• 后序遍历：
  (1)后序遍历左子树；
  (2)后序遍历右子树；
  (3)访问根结点；

   void PostOrder(BTNode *b)
   {  if(b!=NULL)
      {  PostOrder(b->lchild);
         PostOrder(b->rchild);
         printf("%c",b->data);

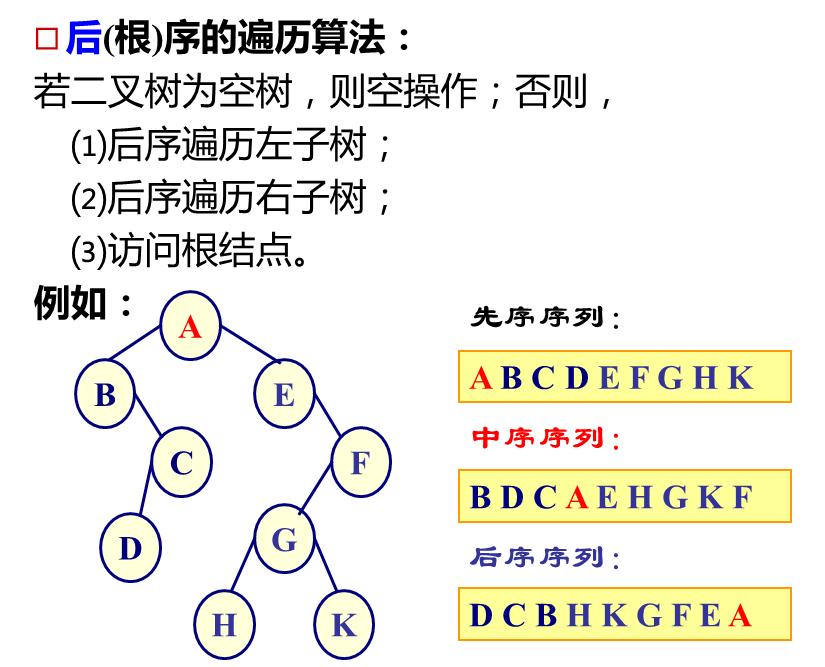
如图所示二叉树三种遍历结果如下：

线索二叉树：

• 遍历二叉树的结果是一个结点的线性序列，可以利用这些空链域存放指向结点的前驱结点和后继结点的地址。当某结点的左指针为空时，令指针指向这个线性序列中该结点的前驱结点（右指针为空则指向后继节点），这些指针为线索。
  创建线索的过程为线索化，线索化的二叉树为线索二叉树。

线索二叉树中，每个结点的储存结构如下图：

中序线索化二叉树的算法如下：

TBTNode* pre;
void Thread(TBTNode*& p)      //对二叉树p进行中序线索化
{
	if (p != NULL)
	{
		Thread(p->lchild);    //左子树线索化
		if (p->lchild == NULL)//左孩子不存在则进行前驱结点线索化
		{
			p->lchild = pre;  //建立前驱结点的后继结点线索
			p->ltag = 1
		}
		else                  //p结点左子树已线索化
			p->ltag = 0;
		if (pre->rchild == NULL)//对pre的后继结点线索化
		{
			pre->rchild = p;    //建立前驱结点的后继结点线索
			pre->lchild = 1;
		}
		else
			pre->rtag = 0;
		pre = p;
		Thread(p->rchild);    //右子树线索化
	}
}
TBTNode* CreateThread（TBTNode* b）//右子树线索化
{
	TBTNode * root;
    root = (TBTNode*)malloc(sizeof(TBTNode));
	root->ltag = 0;
	root->rtag = 1;
	root->rchild = b;
	if (b == NULL)
		root->lchild = root;
	else
	{
		root->lchild = b;
		pre = root;           //pre是结点p的前驱结点，供加线索用
		Thread(b);
		pre->rchild = root;    //加入指向头结点的线索
		pre->rtag = 1;
		root->rchild = pre;    //头结点有线索化
	}
	return root;
}

哈夫曼树：

• 在n个带权叶子结点构成的所有二叉树中，带权路径长度WPL最小的二叉树称为哈夫曼树或最优二叉树。

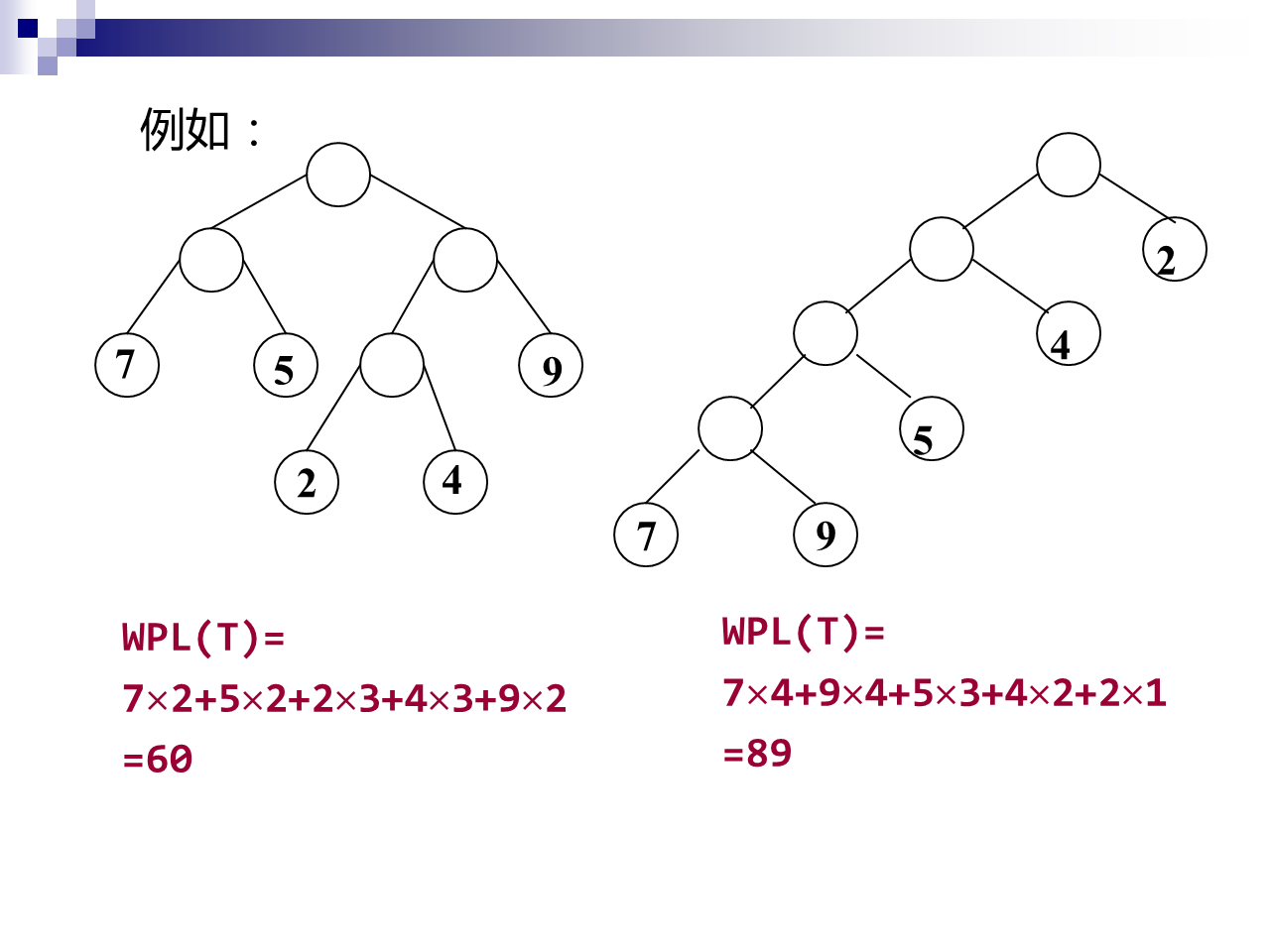
下图为WPL计算过程：

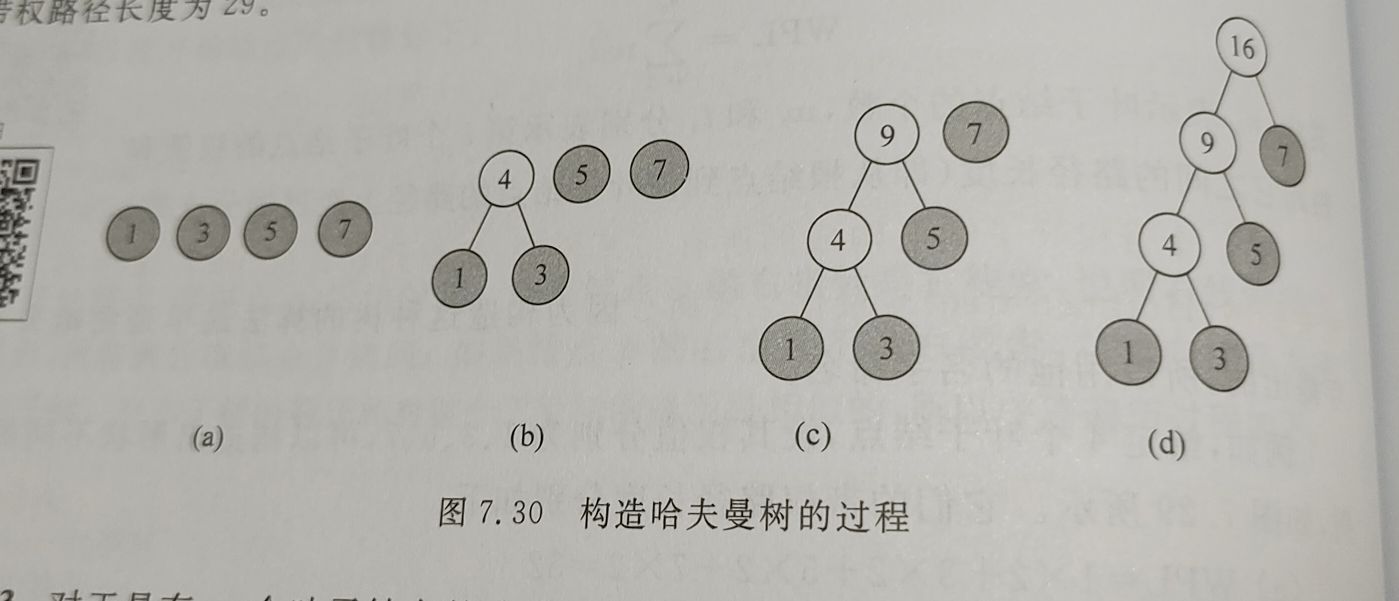
哈夫曼树构造过程：

或总结为，从最小元素作为左右元素，根为两元素之和，依次将元素放置于树中。
图示如下：

下图为构造最优树方法简介：

***存疑：未能理解书中代码，无法实现算法构造哈夫曼树。

树与二叉树

标签：中序   child   长度   线索二叉树   总结   data   算法   哈夫曼树   return   

原文地址：https://www.cnblogs.com/11--1/p/14723008.html