标签:container log 两种 十分 转移 中国剩余定理 div 斐波那契 枚举
良心出题人zhx!!!!
暴力分很满,甚至能到200pts+
预估成绩:\(100+100+100+70 = 370pts\)
最终成绩:\(100+100+60+70 = 330pts\)
排名:\(3/83\)
高精度取模
把字符串倒过来读,边读边取模即可
Description:
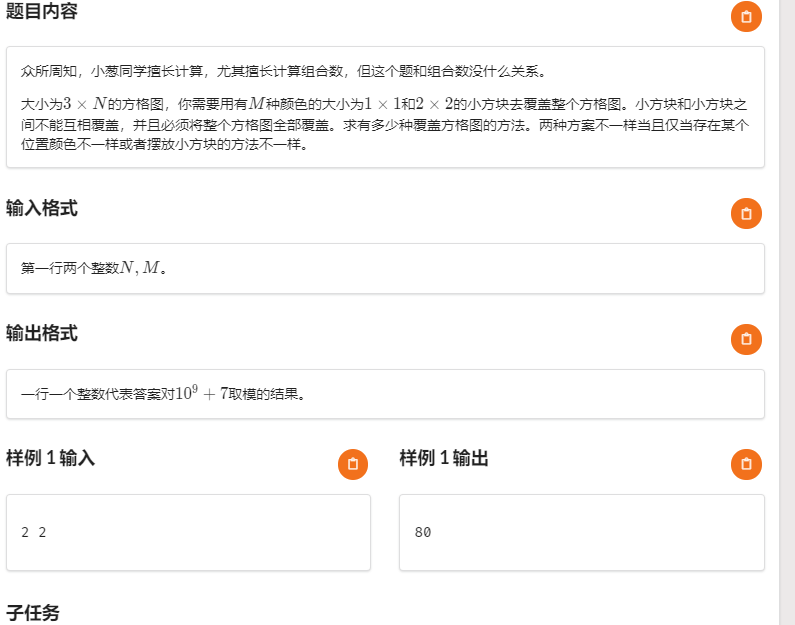
数据范围:\(n,m \le 10^9\)
Solution:
考虑没有颜色的情况:
设 \(f_i\) 表示填到第 \(i\) 列的方案数:
只有两种方块,所以 \(f_i\) 只能从 \(f_{i-1}\) 和 \(f_{i-2}\) 转移过来,考虑转移方案,有转移方程
只有 \(20pts\),考虑涂上颜色。
因为每种颜色可以随便涂,所以一个方块的方案数为 \(m\),发现两次转移都会增加三个块,所以方案数要乘以 \(m^3\),转移方程改为:
现在有 \(70pts\) 了。
发现这个式子很像斐波那契的递推式啊,考虑矩阵加速。列出相关式子,求出转移矩阵
其中 \(Base\) 为
矩阵快速幂转移就好了
Description
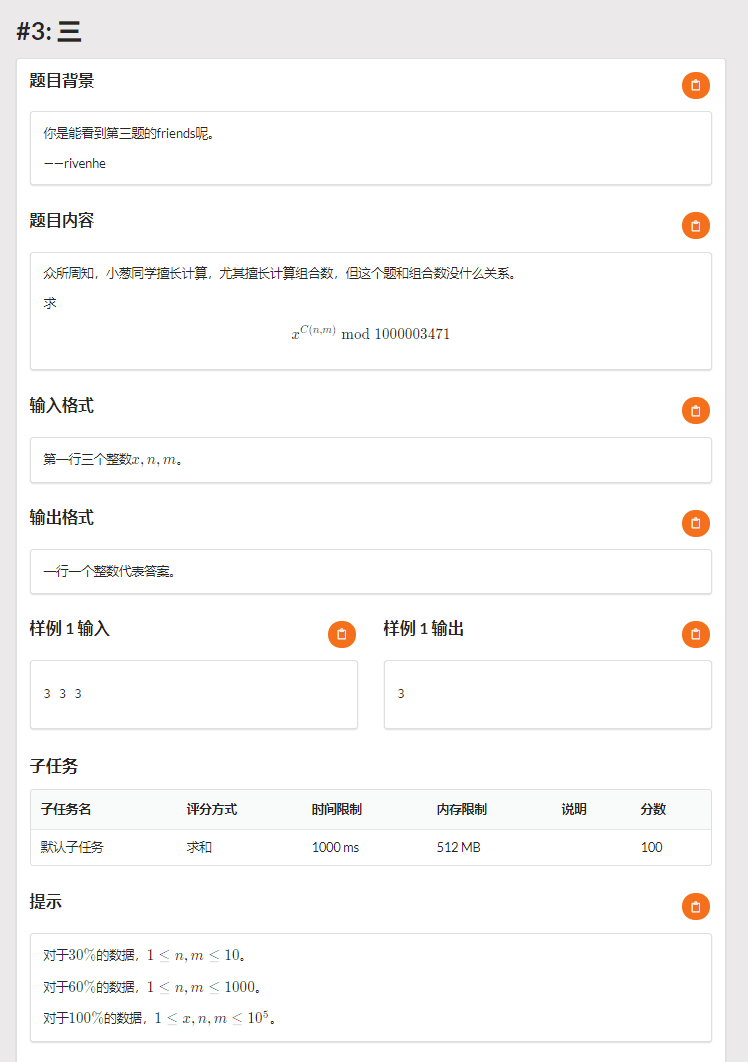
Solution
\(C_n^m\) 在指数上啊
发现后面的模数是质数,所以可以用欧拉定理取模
但是 \(1000003470\) 是个合数,没法求逆元,所以我只写了 \(n,m \le 10^3\) 的递推部分/kk
发现 \(1000003470\) 可以分解为 \(2 \times 3 \times 5 \times 53 \times 677 \times 929\)
所以对于每个质数求一边,然后用中国剩余定理合并即可(或者用扩展卢卡斯)
嗯,我写挂了
Description
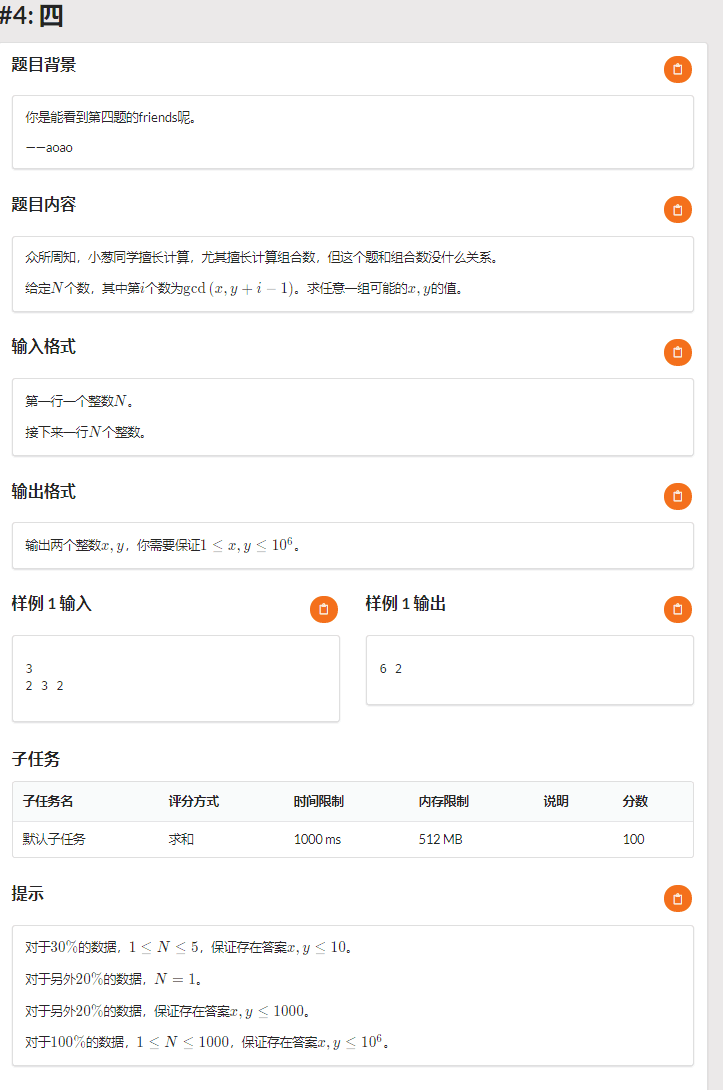
Solution
前三十分暴力判断;
\(N = 1\) 时输出两遍 \(a_1\) 即可;
发现 \(x\) 时不变的,所以存在一个合理的 \(x\) 是所有 \(a_i\) 的最小公倍数,又因为保证 \(y \le 10^3\) 然后枚举就变成 \(O(n^2)\) 的了,可以通过 \(70pts\)
正解不会了/kk
标签:container log 两种 十分 转移 中国剩余定理 div 斐波那契 枚举
原文地址:https://www.cnblogs.com/Silymtics/p/14727911.html