标签:方法 理解 优缺点 core 类别 直方图 能力 训练 参数估计
根据已有知识的表达,针对待识别模式,判别决策其所属类别或者预测其对应的回归值
分为分类和回归两种形式
数学解释:看成一种函数映射f(x),将待识别模式x从输入空间映射到输出空间,f(x)是关于已有知识的表达
模型:关于已有知识的一种表达方式,即函数f(x)
判别函数:使用一些特定的非线性函数实现
判别器:二类分类、多类分类
判别公式和决策边界
特征和特征空间
可理解为“用一组训练样本(数据)学习模型的参数和结构”
分为线性模型和非线性模型
样本量N与模型参数M的关系(参考线性代数-解方程组):
N=M唯一的解
N>>M没有准确的解
N<<M无数个解/无解
机器学习流程
目标函数、优化算法
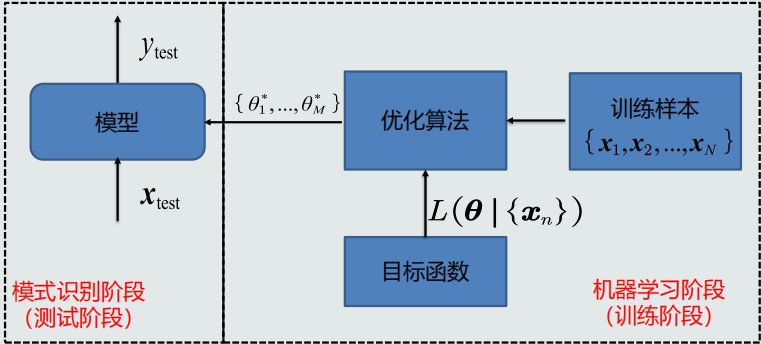
机器学习方式
监督式学习、无监督式学习、半监督式学习、强化学习
泛化能力:训练得到的模型不仅要对训练样本具有决策能力,也要对新的(训练过程中未看见)的模式具有决策能力
泛化能力低:过拟合
提高方法:模型选择(固定训练样本个数选择合适的多项式阶数M)、正则化(在目标函数中加入正则项)
问题1:如何计算单个向量到多个向量的距离?
答:按均值或者按最近邻计算
问题2:计算测试样本到类的何种距离?
答:前提:应满足同一性、非负性、对称性、三角不等式
? 欧式距离 sqrt(∑(xi-zi)**2) = sqrt((X-Z).T * (X-Z))
? 曼哈顿距离 ∑|xi-zi| = |X-Z|
? 加权欧式距离 sqrt(∑wi*(xi-zi)**2) = sqrt((X-Z).T * Iw * (X-Z))
解耦
即实现协方差矩阵对角化,去除特征之间的相关性
求解 W1*∑x*W1.T=∧(对角阵)中 W1 ,经过一系列的推演可得W1=∑x的正交单位化的特征向量组成的矩阵
转换前后欧式距离保持一致,故说明W1 只是起了旋转的作用
白化
即将对角矩阵尺度变化成单位矩阵,使所有特征具有相同的方差
求解 W2*∧*W2.T=I(单位矩阵)中 W2,经过一系列的推演可得 W2 = ∧的-1/2次方
最终求得映射矩阵W=W2*W1
后验概率(P(Ci|x):类别输出C、输入模式x):用于分类决策,表达给定模式x属于类Ci的可能性
观测似然概率(P(x|Ci))、先验概率(P(Ci))、边缘概率(P(x))
P(Ci|x)=(P(x|Ci)*P(Ci))/P(x)
MAP分类器(最大后验概率分类器)
即将测试样本决策分类给后验概率最大的那个类
判别公式、决策边界(二类分类; 单维空间:通常有两条决策边界,高维空间:复杂的非线性边界)
决策误差(概率误差=未选择的类对应所对应的后验概率)
MAP分类器决策目标即为最小化概率误差,即分类误差最小化
(给定所有测试样本,MAP分类器选择后验概率最大的类,等于最小化平均概率误差,即最小化决策误差)
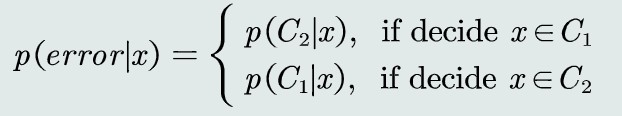
观测概率:单维高斯分布
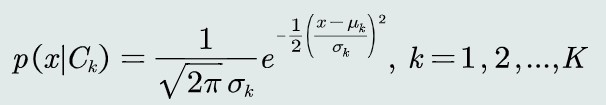
决策边界:
当???? = ???? = σ 时,决策边界是线性的,只有一条;
如果???? < ????,且?? ???? < ?? ???? ,则?? < 0;
说明:在方差相同的情况下,MAP决策边界偏向先验可能性较小的类,即分类器决策偏向先验概率高的类
当???? ≠ ????时,决策边界有两条(非线性边界),该决策方程是关于??的二次型函数
且若???? > ????及先验概率相等时,可知?? > 0,分类器倾向选择????类,即方差较小(紧致)的类
MAP分类器偏向于先验较大可能性、分布较为紧致的类
观测概率:高维高斯分布
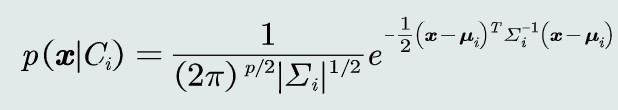
决策边界为一个超二次型
贝叶斯决策不能排除出现错误判断的情况,由此会带来决策风险。更重要的是,不同的错误决策会产生程度完全不一样的风险;
损失( λ(αi|Cj)(决策动作αi|Cj、测试样本的真值Cj) )
决策风险 R(αi|x)
R(αi|x) = ∑λij*P(Cj|x)
贝叶斯分类器
给定一个测试样本??,贝叶斯分类器选择决策风险最小的类;
贝叶斯分类器=MAP分类器+决策风险因素
判别公式
决策损失: 给定单个测试样本,贝叶斯决策的损失就是决策风险R
对于所有测试样本,期望损失为所有样本决策损失之和
决策目标:最小化期望损失
朴素贝叶斯分类器
特征维度太高,通过即假设特征之间符合独立同分布以达到简化计算的目的
拒绝选项
监督式学习
最大似然估计

先验概率估计: 给定所有类的??个训练样本,假设随机抽取其中一个样本属于??1类的概率为??,则选取到??1个属于??1类样本的概率为先验概率的似然函数(即目标函数)
为最大化似然函数,采用对参数P求偏导
先验概率的最大似然估计就是该类训练样本出现的频率
观测概率估计: 如果观测似然概率服从高斯分布,待学习的参数包含该高斯分布的均值??和协方差??(观测似然概率是关于单个类的条件概率)
为最大化似然函数,采用对两个参数??和??分别求导
高斯分布均值的最答似然估计等于样本的均值,高斯分布协方差估计等于所有训练模式的协方差
无偏估计
高斯分布协方差的最大似然估计式有偏估计
需对协方差估计进行修正
可以通过将训练样本的协方差乘以??/(?? ? 1)来修正协方差的估计值
贝叶斯估计:给定参数??分布的先验概率以及训练样本,估计参数θ分布的后验概率

假设??服从一个概率分布:
参数的后验概率
总结:
贝叶斯估计的步骤

贝叶斯估计等是假设概率分布为高斯分布,但如果分布未知,就需要使用无参数估计技术来实现概率密度估计
常用的无参数估计技术:KNN估计、直方图估计、核密度估计,基于p(x)=k/(NV)估计概率密度
给定x,找到其对应的区域R时期包含k个训练样本,以此计算P(x)
概率密度估计表达(dk(x)为 k个样本与x距离):
P(x)≈k/(2Ndk(x))
当训练样本个数N越大,k取值越大,概率估计越准确
优缺点
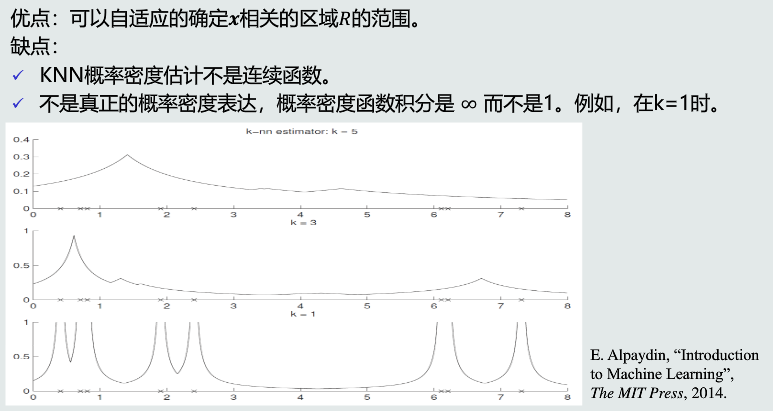
? 原理

? 优缺点

? 原理

? 优缺点

标签:方法 理解 优缺点 core 类别 直方图 能力 训练 参数估计
原文地址:https://www.cnblogs.com/hyuqi/p/14728946.html