标签:作用 总结 技术 aoe 最长路 两种 项目 test 相同
AOE寻找关键路径的核心思想就是寻找事件和活动的最早时间和最晚时间(earlist time ,latest time),节点(事件)和边(活动)的最早、最晚时间分别缩写为etv,ltv,ete,lte(编程时候,也有用ve,vl,ee,el代替的)。关于最短时间最晚时间的取值,经常会有误解,我们不妨简化问题(我相信任何复杂的问题,都可以简化为简单的问题并入手分析)。
假如甲乙两个人被领导分配工作,协同完成某一项工作,其中,领导分配工作用时10分钟,甲完成他负责的工作用了50分钟,乙完成他负责的工作,用了70分钟。这个工程可以用AOE图表示如下:
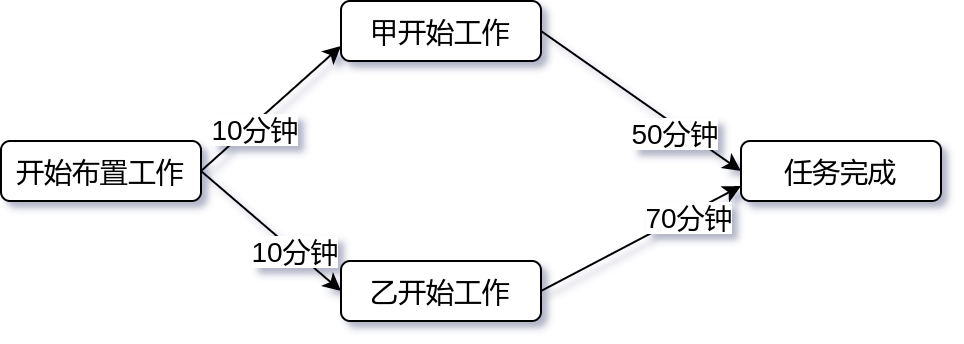
现在问,事件“人物完成”最早需要多长时间?显然应该是10+70=80分钟,而不是10+50=60分钟,因为就算甲完成的早,但是有乙这个队友拖后退(也许是乙的任务难度更大,题外话),整个任务最早也是80分钟后完成,了解这个有人么用呢?可以了解是哪一个环节(活动)托慢了整个任务的效率,进而做改进。
现在我们知道了整个任务最快需要80分钟,我们可以把最终的任务实践看作一个大的工程的某一个环节(事件),则每一个事件的最早发生时间,其实也就是最长的时间。
我们把数据做一个简单的记录:
开始节点的最早发生时间:0
甲开始工作的最早发送时间:10,甲用时50分钟
乙开始工作的最早发送时间:10,乙用时70分钟
任务最早完成时间:80分钟。
现在问:甲工作的最迟发生时间是在几分钟?我们知道,在整个工程的最短80分钟时间内,乙一直在不停的工作,而甲呢,做完后,则可以休息20分钟,当然,甲也可以拖拖拉拉的做,用70分钟做完自己本可以50分钟做完的事情,甚至甲可以休息20分钟后再接着工作,丝毫不影响整个任务的时间进度。这就是说,甲最迟的开始时间可以是20分钟后,等于80-50=30,这就是反方向,从最后一个节点向前推。
我们接着把问题再稍稍的复杂一点点,看下面这个图,我们只看图中红色圈起来的部分。
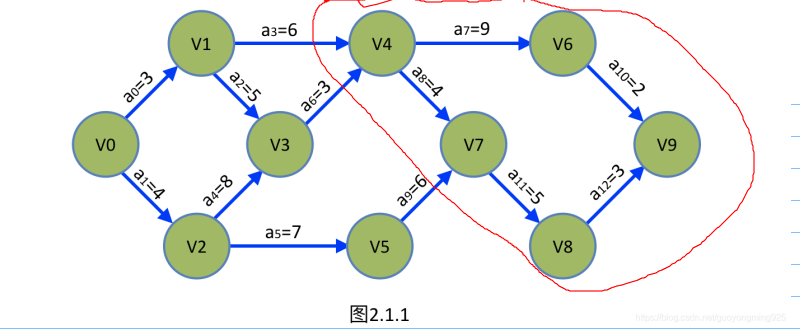
假设V4的最早发生时间是第15分钟,整个工程的最早完成时间是27分钟,那么问,V4的最晚发生时间是第几分钟?
这里V4到终点分为两个路线,我们把两个路线的节点直接忽略,而把中间的边的权重相加,变成:下图:
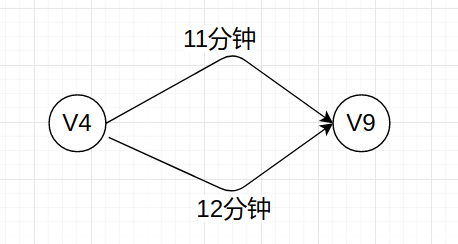
相当于V4开始有两种路线可以到达V9,耗时分别是11和12。这时候,如果问V4的最晚发生时间是第几分钟?如果我们用27-11=16,认为V4的最晚发生时间是第16分钟,那么v4如果在第16分钟开始按照下面的方案工作,则最终完成时间就是27分钟,显然托慢了工程的进度,是不正确的,正确的应该是27-12(最长路线)=15分钟,也就是说:倒推最迟发生时间的时候,是减去最大值。
然后我们就可以自己动手,写出上面图中V0----V9所有事件的最早发生时间和最晚发生时间。写一下,看看和我写的一样不一样:

现在找一下关键路径的点,看一下是不是我红线沿途画的这几个点:
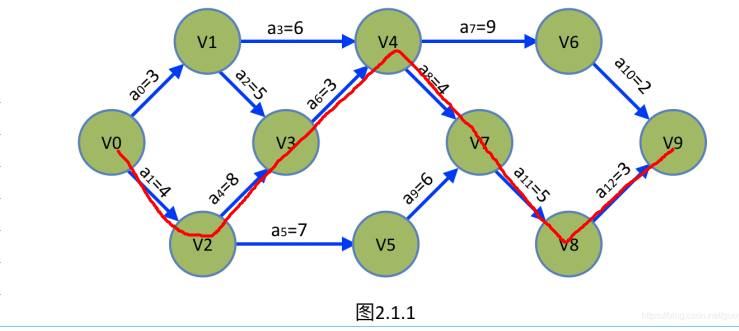
有没有发现,关键路径上的事件,他们的最早发生时间和最晚发生时间大小都是一致的?
注意,起始节点的最早和最迟都是0,结束节点的最早和最迟也相等,都是项目的最短时间(最大值)。
我们先把上面的思路总结成下面的公式,这是编程判断的基础:

是不是觉得自己可以绞尽脑汁写代码找出关键路径了?别急,知道这些信息还不够,如果有多个关键路径,仅仅根据节点是看不出关键路径的。你还需要知道活动的最早开始时间和最迟开始时间。
活动就是在节点<Vj,Vk>之间的一条有向线。活动的最早开始时间,显然就是有向线的起始节点Vj的最早开始时间(也是之前最长活动时间的和),而活动的最迟发生时间,则和节点的算法类似,也是从工程的最早结束时间倒着推,一步步的减去最大值。
假设节点V[i]----->V[j]之间的活动是e[k],则活动e[k]的最晚开始时间,就是V[j]的最晚开始时间,减去活动的时间:公式:为
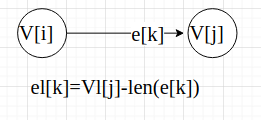
这个公式,可以只用两个节点的图分析一下,应该能够分析出来。
如此,你试试写出来上面图中所有节点和边的最早和最晚时间。看看是不是下面这样子

上图中,我把最早和最迟时间相同的节点和边,用黄颜色填充,以便更醒目。
这样子,我们就手工找到了关键路径以及路径上的节点。
下一篇随笔将讨论如何编程实现这个算法思路
标签:作用 总结 技术 aoe 最长路 两种 项目 test 相同
原文地址:https://www.cnblogs.com/svod5306/p/14728656.html