标签：组合   完成   描述   如何   问题：   函数   span   表示   结束   

1. 问题

l 一般性描述：

设m元钱，n项投资，函数fi(x)表示将x元投入第i项项目所产生的效益，i=1,2,…,n

问：如何分配这m元钱，使得投资的总效益最高？

l 组合优化问题：

假设分配给第i个项目的钱数是Xi，问题描述为：

目标函数 max{f1(x1)+f2(x2)+…+fn(xn)}

约束条件 x1+x2+…+xn=m,xi∈N

实例：

投资x万元 效益f1(x)万元 f2(x)  f3(x)     f4(x)

0              0           0      0      0

1              11           0      2     20

2              12           5      10     21

3              13           10  30     22

4              14           15  32     23

5              15           20  40     24

2. 解析

l 递推公式

设Fk(x)表示x万元投给前k个项目的最大效益，k=1,2,…,n,x=1,2,…,m

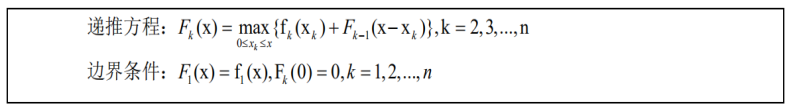
说明：第k步，前后共分配x万元

分配给第k个项目为xk；

x-xk万元，分配给前k-1个项目

l 证明满足优化原则

优化原则：一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列。

已知：这个序列L1是最优决策序列

那么：这个序列任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列。

证明（反证法）：

模板：

实例：

如L=f1(x1)+f2(x2)+f3(x3)+f4(x4)+f5(x5)

L1=f1(x1)+f2(x2)+f3(x31)+f4(x4)+f5(x5)

s1=f2(x2)+f3(x31)+f4(x4)

s2=f2(x2)+f3(x32)+f4(x4)

L2=f1(x1)+f2(x2)+f3(x32)+f4(x4)+f5(x5)

其中L中x3可取x32和x32，当取x31时，L的最大值为L1

3.设计

递推方程：

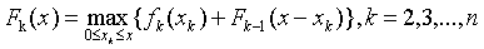
边界方程：

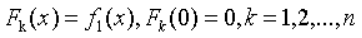
xi（x）=k：新加第i项时，总共分配x元时，第i项分配了k元（xk）

for k=1,2,3,...,n

for x=1,2,3,...,m

for xk=0,1,2,3,...,x

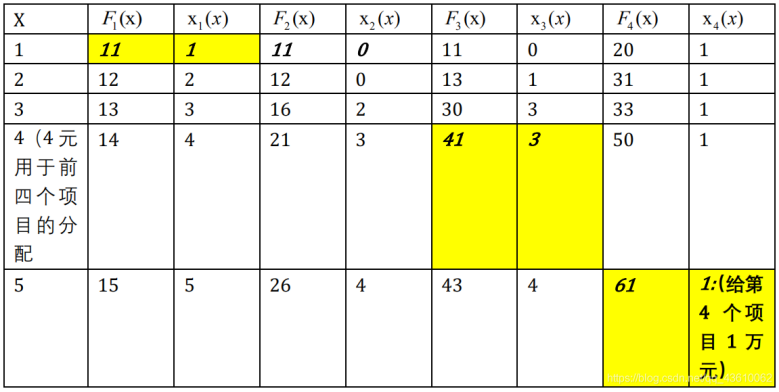
x2(1)=0表示在总共分配1万元时，取得最大效益11万元时分配给第二个项目的钱数是0

完成如下表格：

4.分析

投资问题

标签：组合   完成   描述   如何   问题：   函数   span   表示   结束   

原文地址：https://www.cnblogs.com/zs0618/p/14748823.html