H Infinity contrl ---LMI方法（Yalmip 求解）和Riccati 方法

时间：2021-05-24 13:13:46 阅读：0 评论：0 收藏：0 [点我收藏+]

标签：反馈 wro real method ica 技术利用 sigma hsv

H Infinity contrl ---LMI方法（Yalmip 求解）和Riccati 方法

参考书籍：Yu, Hai-Hua_ Duan, Guangren - LMIs in control systems _ analysis, design and applications (2013, CRC Press) - libgen.lc(一书的附录有详细介绍LMI的编写方式-有很多例子)

参考网站：http://www.doc88.com/p-8718494012962.html

:YALMIP

Download - YALMIP

有问题可以上google论坛--再matlab 问答模块可以搜到网址--可以提问相关问题，

关于LMI 本身求解参考：

线性矩阵不等式(LMI)的_MATLAB求解- http://www.doc88.com/p-7874379836838.html

Matlab中LMI(线性矩阵不等式)工具箱使用教程 https://www.doc88.com/p-304944065894.html

线性矩阵不等式的LMI工具箱求解-LMI三个函数的应用实例； https://www.doc88.com/p-3925042294217.html

https://www.doc88.com/p-660150804881.html

https://blog.csdn.net/qq_28093585/article/details/69358180

ceshi_Hinf_lmi

clc;clear; close all;
A  = [2 1 -2;1 -1 -3; 4 0 -1];
B = [1 0;0 3;3 1];
E1 = [1 0.2 -0.5]‘;
C = [2 1 -0.5];
D = [1 1];
E2 = [0.05]

P = 10e+7;
X0 = [8.7047 -6.5321 4.2500;
     -6.5321 8.8601 -4.2821;
     4.2500 -4.2821 5.0227];
W0 = [-5.2786 2.9364 -7.7991;
      -3.4736 -0.8733 6.0925];
W =P*W0; X = X0*P;
K1 =W*inv(X)

Ac =A-B*K1;
Bc = B;
Cc = C;
Dc = D;
sys_cl = ss(Ac,Bc,Cc,Dc);
step(sys_cl)
% figure(1)
% t = 0:0.01:15;
% r =[0.5*ones(size(t));
%     0.5*ones(size(t))];
% [y,t,x]=lsim(sys_cl,r,t);
% plot(t,y)
% 
% 
% K2 = [1.2850 0.5978 -2.0283;
%      -1.4101 -0.7807 1.4861]
% Ac =A-B*K2;
% Bc = B;
% Cc = C;
% Dc = D;
% sys_cl = ss(Ac,Bc,Cc,Dc);
% 
% figure(2)
% t = 0:0.01:15;
% r =[0.5*ones(size(t));
%     0.5*ones(size(t))];
% [y,t,x]=lsim(sys_cl,r,t);
% plot(t,y)

View Code

%连续H2 optimal control 
clc;clear;close all;

%% 书籍：LMIs in control systems _ analysis, design and applications中428页中例题的结果--
% 连续H2 state feedback control
% Step 1. Describe this LMIs in MATLAB  网址：http://www.doc88.com/p-8718494012962.html
%{
% Step 1. Describe this LMIs in MATLAB
% specify parameter matrices
A = [-3 -2 1;1 2 1;1 -1 -1]; B1 = [1; 0; 1];
B2 = [2 0;0 2;0 1]; C = [1 0 1;0 1 0]; D = eye(2);
% define the LMI system
setlmis ([]) % initialing
% declare the LMI variable
X = lmivar(1, [3 1]); W = lmivar(2,[2,3]);
Z = lmivar(1, [2 1]); rou = lmivar(1, [1 1]);
% #1 LMI, left-hand side
lmiterm ( [1 1 1 X],A, 1, ‘s‘);
lmiterm ( [1 1 1 W],B2, 1, ‘s‘);
lmiterm ( [1 1 1 0],B1*B1‘);
% #2 LMI, left-hand side
lmiterm ( [2 1 1 Z],1,-1); % the (1,1) block
lmiterm ( [2 1 2 W],D,1); % the (1,2) block
lmiterm ( [2 1 2 X],C,1); % the (1,2) block
lmiterm ( [2 2 2 X],1,-1); % the (2,2) block
% #3 LMI, left-hand side
lmiterm ( [3 1 1 Z],[1 0],[1 0]‘);
lmiterm ( [3 1 1 Z],[0 1],[0 1]‘);
% #3 LMI, right-hand side
lmiterm ( [3 1 1 rou],1,-1);
lmisys=getlmis; % finishing description
% Step 2. Solve this LMI problem and use dec2mat to get the
% corresponding matrix X
% c = mat2dec(lmisys,0,0,ones(2)); % obtain vector c
n=decnbr(lmisys);%获取LMI中决策变量的个数
c=zeros(n,1);
% for jj=1:n
%     [Zj]=defcx(lmisys,jj,Z);
%     c(jj)=trace(Zj)
% end
for jj=1:n
    [pj]=defcx(lmisys,jj,rou);
    c(jj)=(pj);
end
options=[1e-5 0 0 0 1];
%[copt,xopt] = mincx(lmisys,c);
[copt,xopt] = mincx(lmisys,c,options); % solve the optimization problem
X = dec2mat(lmisys,xopt,1); % extract matrix X
W = dec2mat(lmisys,xopt,2); % extract matrix W
Z = dec2mat(lmisys,xopt,3); % extract matrix Z
K = W*inv(X); % get the feedback gain
%}
%注：求出的结果为：[-1.00000000000000,5.44822811876415e-18,-1.00000000000000;
%               1.75680133525483e-16,-1.00000000000000,-7.35314080057690e-18]
% 书中的结果是[-1 0 -1;0 -1 0]

%%
%{
%% 书籍：LMIs in control systems _ analysis, design and applications中259页中例题的结果
% Step 1. Describe this LMIs in MATLAB  网址：http://www.doc88.com/p-8718494012962.html
% specify parameter matrices
A = [-3 -2 1;1 2 1;1 -1 -1]; B1 = [3; 0; 1];%干扰矩阵
B2 = [2 0;0 2;0 1]; %控制矩阵
C = [1 0 1;0 1 1]; D = [1 1;0 1];
% define the LMI system
setlmis ([]) % initialing
% declare the LMI variable
X = lmivar(1, [3 1]); W = lmivar(2,[2,3]);
Z = lmivar(1, [2 1]); rou = lmivar(1, [1 1]);
% #1 LMI, left-hand side
lmiterm ( [1 1 1 X],A, 1, ‘s‘);
lmiterm ( [1 1 1 W],B2, 1, ‘s‘);
lmiterm ( [1 1 1 0],B1*B1‘);
% #2 LMI, left-hand side
lmiterm ( [2 1 1 Z],1,-1); % the (1,1) block
lmiterm ( [2 1 2 W],D,1); % the (1,2) block
lmiterm ( [2 1 2 X],C,1); % the (1,2) block
lmiterm ( [2 2 2 X],1,-1); % the (2,2) block
% #3 LMI, left-hand side
lmiterm ( [3 1 1 Z],[1 0],[1 0]‘);
lmiterm ( [3 1 1 Z],[0 1],[0 1]‘);
% #3 LMI, right-hand side
lmiterm ( [3 1 1 rou],1,-1);
lmisys=getlmis; % finishing description
% Step 2. Solve this LMI problem and use dec2mat to get the
% corresponding matrix X
% c = mat2dec(lmisys,0,0,ones(2)); % obtain vector c
n=decnbr(lmisys);%获取LMI中决策变量的个数
c=zeros(n,1);
% for jj=1:n
%     [Zj]=defcx(lmisys,jj,Z);
%     c(jj)=trace(Zj)
% end
for jj=1:n
    pj=defcx(lmisys,jj,rou);
    c(jj)=(pj);
end
%options=[1e-5 0 0 0 1];
[copt,xopt] = mincx(lmisys,c);
%[copt,xopt] = mincx(lmisys,c,options) % solve the optimization problem
X = dec2mat(lmisys,xopt,1) % extract matrix X
W = dec2mat(lmisys,xopt,2) % extract matrix W
Z = dec2mat(lmisys,xopt,3) % extract matrix Z
K = W*inv(X) % get the feedback gain
%}
%注：求出的结果为：K =[-0.911192567348860,1.75193380502826,-0.249064838067320;
%                     -0.106341894142934,-1.90039834212258,-0.701758897247713];
%                      pou =3.349135e-04;
%书中的结果：[-0.9112 1.7519 -0.2491; -0.1063 -1.9004 -0.7018];



%% 采用yample优化工具箱的求出结果；
%示例 https://github.com/eoskowro/LMI
% Arizona State University
% MAE 598 LMIs in Control Systems
%{
clear;close all; clc
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMI for Opimal FSF H_2 Control
% Bring in Data
A = [-1 1 0 1 0 1;...
    -1 -2 -1 0 0 1;...
    1 0 -2 -1 1 1;...
    -1 1 -1 -2 0 0;...
    -1 -1 1 1 -2 -1;...
    0 -1 0 0 -1 -3];
B = [0 -1 -1;...
    0 0 0;...
    -1 1 1;...
    -1 0 0;...
    0 0 1;...
    -1 1 1];
C = [0 1 0 -1 -1 -1;...
    0 0 0 -1 0 0;...
    1 0 0 0 -1 0];
D = zeros(3);

% Determine sizes
ns = size(A,1);   % number of states
nai = size(B,2);  % number of actuator inputs
nmo = size(C,1);  % number of measured outputs
nd = nai+nmo;     % number of disturbances
nro = nmo+nai;    % number of regulated outputs
eta = 0.0001;

% 9 Matrix Representation
B1 = [B zeros(ns,nmo)];
B2 = B;
C1 = [C;...
     zeros(nai,ns)];
C2 = C;
D11 = [D zeros(nai);...
      zeros(nmo) zeros(nmo)];
D12 = [D;...
      eye(nmo)];
D21 = [D eye(nmo)];
D22 = D;

% Settings
opt = sdpsettings(‘verbose‘,0,‘solver‘,‘sedumi‘); %Create/alter solver options structure.

% Define Variables
gam= sdpvar(1);
X = sdpvar(6);
W = sdpvar(6);
Z = sdpvar(3,6);

% Define matricies
mat1 = [A B2]*[X;Z] + [X Z‘]*[A‘;B2‘]+ B1*B1‘;
mat2 = [X (C1*X+D12*Z)‘;C1*X+D12*Z W];
mat3 = trace(W);

% Define Constraints
F = [];
F = [F, X>=eta*eye(6)];
F = [F, mat1<=-eta*eye(6)];
F = [F, mat2>=eta*eye(12)];
F = [F, mat3<=gam];

% Optimization Problem
optimize(F,gam,opt);
gam= sqrt(gam);
disp(‘The H-2 gain is: ‘);
disp(value(gam));
K= value(Z)*inv(value(X));
sys = ss(A,B,C,D)
eig(A+B2*K) %求出的系统是稳定的的
%}



%% 

%使用上面书中例题的参数的采用Yamiple求解-采用的公式也与上面的相同
A = [-3 -2 1;1 2 1;1 -1 -1]; B1 = [3; 0; 1];%干扰矩阵
B2 = [2 0;0 2;0 1]; %控制矩阵
C1 = [1 0 1;0 1 1]; D12 = [1 1;0 1];
eta = 0.000001; %当减小eta的值时，求出的K值几乎和书中例题结果一样

% Settings
opt = sdpsettings(‘verbose‘,0,‘solver‘,‘sedumi‘); %选定那种求解器

% Define Variables
gam= sdpvar(1);
X = sdpvar(3);
W = sdpvar(2,2);
Z = sdpvar(2,3);

% Define matricies
mat1 = [A B2]*[X;Z] + [X Z‘]*[A‘;B2‘]+ B1*B1‘;
mat2 = [X (C1*X+D12*Z)‘;C1*X+D12*Z W];
mat3 = trace(W);

% Define Constraints
F = [];
F = [F, X>=eta*eye(3)];
F = [F, mat1<=-eta*eye(3)];
F = [F, mat2>=eta*eye(5)];
F = [F, mat3<=gam];

% Optimization Problem
optimize(F,gam,opt);
gam= sqrt(gam);
disp(‘The H-2 gain is: ‘);
disp(value(gam));
K = value(Z)*inv(value(X));
X = value(X)
Z = value(Z)
W = value(W) %注意这里的W和Z与上面方法的W和Z刚好是相反的
gama =value(gam)
sys = ss(A,B2,C1,D12)
eig(A+B2*K) %求出的系统是稳定的的

%注：当eta = 0.000001;时得出的K值为：[-0.911539661339165,1.74872193348681,-0.247991715575816;-0.105965874043457,-1.89693739748588,-0.702917300903666]
% 几乎和书中例题一样但是求出的gamma值相差较大：书中259页给出的时3.3491*10^(-4)
% 而这种方法求出的gamma值为： 0.0184

%{
%% 连续的H2 optimal control --表达公式不同采用Yamiple方法
% 参考的：LMI Properties and Applications in Systems, stabillity and  Control
% theory(好)70页公式（4.4，4.6，4.7）
clear;
clc;
A = [-3 -2 1;
      1 2 1;
    1 -1 -1];
B1 = [1 0.2 0]‘;
B2 = [0.4 1 0.6]‘;
C1 = [1.2 0.5 0.3];
D12 = 1;

P = sdpvar(3);
Z = sdpvar(1);
F = sdpvar(1,3);
mu = sdpvar(1);
mat1 = [A*P+P*A‘+B2*F+F‘*B2‘  P*C1‘+F‘*D12‘;
       (P*C1‘+F‘*D12‘)‘            -eye(1)];
mat2 = [Z B1‘;
        B1 P];
Fd = [mat1<=0; mat2>=0; P>=0; Z>=0 ;trace(Z)<=mu];
optimize(Fd, mu);
Kd = value(F)*inv(value(P))
H2_norm = sqrt(value(mu))
%}



%{
%%  连续的H2全状态反馈 --LMI原始方法-只是表达式与上面的形式不同【验证】
% 参考的：LMI Properties and Applications in Systems, stabillity and  Control
% theory(好)70页公式（4.4，4.6，4.7）

A = [-3 -2 1;1 2 1;1 -1 -1]; B1 = [1; 0; 1];
B2 = [2 0;0 2;0 1]; C1 = [1 0 1;0 1 0]; D12 = eye(2);D11=[0;0];

 %构建矩阵变量  
  [M,N] =size(A);
  setlmis([]);     
  P=lmivar(1,[N,1]); %N阶对称满块     
  Z=lmivar(1,[1,1]);    
  F=lmivar(2,[2,N]);
  rou=lmivar(1,[1,1]);
  %描述LMI
  %第一个LMI
  lmiterm([1,1,1,P],A,1,‘s‘); %AP+(AP)‘     
  lmiterm([1,1,1,F],B2,1,‘s‘); %B2*F+(B2*F)‘     
  lmiterm([1,1,2,P],1,C1‘);    %P*C1     
  lmiterm([1,1,2,-F],1,D12‘);  %F‘*D12‘     
  lmiterm([1,2,2,0],-eye(2));   %I     

   %第二个LMI
  lmiterm([-2,1,1,Z],1,1);%Z
  lmiterm([-2,1,2,0],B1‘);%B1‘
  lmiterm([-2,2,2,P],1,1);%P
  %第三个LMI --迹的表达形式
%   lmiterm ([3 1 1 Z],[1 0],[1 0]‘);
%   lmiterm ([3 1 1 Z],[0 1],[0 1]‘);
  lmiterm ([3 1 1 Z],1,1);
  lmiterm ([-3 1 1 rou],1,1);  
  lmisys=getlmis ;%获取lmi信息 
  
  n=decnbr(lmisys);  %得出决策变量的个数  
  c=zeros(n,1);     
  for j=1:n         
      bj=defcx(lmisys, j, rou);    
      c(j)=bj;     
  end
 % options=[1e-5, 0, 0, 0, 0]; %计算精度     
 [copt,xopt]=mincx(lmisys,c );
%  P=dec2mat(lmisys, xopt, P); 
%  Z=dec2mat(lmisys, xopt, Z);
%  W=dec2mat(lmisys, xopt, W); 
 X = dec2mat(lmisys,xopt,1); 
 F = dec2mat(lmisys,xopt,2);  
 Z = dec2mat(lmisys,xopt,3);
 K = F*inv(P)
 gamma=sqrt(copt)
  %}
  
%{  
%% 连续的H2 optimal control 
clear;
clc;
A = [-3 -2 1;1 2 1;1 -1 -1]; B1 = [1; 0; 1];
B2 = [2 0;0 2;0 1]; C1 = [1 0 1;0 1 0]; D12 = eye(2);D11=[0;0];
P = sdpvar(3);
Z = sdpvar(1);
F = sdpvar(2,3);
musqr = sdpvar(1);
mat1 = [A*P+P*A‘+B2*F+F‘*B2‘  P*C1‘+F‘*D12‘;
       (P*C1‘+F‘*D12‘)‘            -eye(2)];
mat2 = [Z B1‘;
        B1 P];
Fd = [mat1 <= 0; mat2>=0; P>=0; Z>=0 trace(Z)<=musqr];
optimize(Fd, musqr);
Kd = value(F)*inv(value(P))
H2_norm = sqrt(value(musqr))
%}

%{
%% 离散的H2 ---采用传统的LMI方法
% 参考的：LMI Properties and Applications in Systems, stabillity and  Control
% theory(好)70页公式（下半部的公式）

clear;
clc;
A = [0.1 0.2 0.3;
     0.4 0.5 0.6;
     0.7 0.8 0.9];
B1 = ones(3,1);
B2 = ones(3,1);
C1 = ones(1,3);
D12 = 1;

%构建矩阵变量  
  [M,N] =size(A);
  setlmis([]);     
  P=lmivar(1,[N,1]); %N阶对称满块     
  Z=lmivar(1,[1,1]);    
  F=lmivar(2,[1,N]);
  rou=lmivar(1,[1,1]);
  %描述LMI
  
  %第一个LMI
  lmiterm([-1,1,1,P],1,1);  %P    
  lmiterm([-1,1,2,P],A,1);  %AP    
  lmiterm([-1,1,2,F],B2,1); %B2*F     
  lmiterm([-1,1,3,0],B1);   %B1     
  lmiterm([-1,2,2,P],1,1);   %P     
  lmiterm([-1,2,3,0],0);     %0
  lmiterm([-1,3,3,0],eye(1)); %I

  %第二个LMI
  lmiterm([-2,1,1,Z],1,1);%Z
  lmiterm([-2,1,2,P],C1,1);%C1*P
  lmiterm([-2,1,2,F],D12,1);%d112*F
  lmiterm([-2,2,2,P],1,1);  %P  
  
  %第三个LMI --迹的表达形式
% lmiterm ([3 1 1 Z],[1 0],[1 0]‘);
% lmiterm ([3 1 1 Z],[0 1],[0 1]‘);
  lmiterm ([3 1 1 Z],1,1);
  lmiterm ([-3 1 1 rou],1,1); 

% 两个约束条件
  lmiterm([-4,1,1,P],1,1); %P正定P>0
  lmiterm([-5,1,1,Z],1,1); %Z正定Z>0
  lmisys=getlmis ;%获取lmi信息 
  
  n=decnbr(lmisys);  %得出决策变量的个数  
  c=zeros(n,1);     
  for j=1:n         
      bj=defcx(lmisys, j, rou);    
      c(j)=bj;     
  end
 % options=[1e-5, 0, 0, 0, 0]; %计算精度     
 [copt,xopt]=mincx(lmisys,c );
 
 %注意获取参数时要按照定义变量的顺序进行
%  P=dec2mat(lmisys, xopt, P); 
%  Z=dec2mat(lmisys, xopt, Z);
%  W=dec2mat(lmisys, xopt, W); 
 P = dec2mat(lmisys,xopt,1);

 F = dec2mat(lmisys,xopt,3);  

 K = F*inv(P)
 gamma=sqrt(copt)
%}

H Infinity control LMI 方法

参考：H∞控制器的设计 - 百度文库 (baidu.com)

技术图片

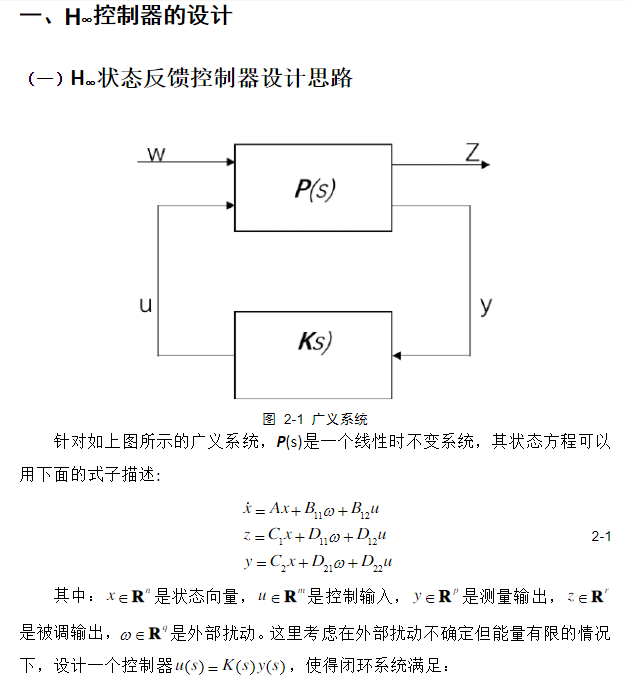
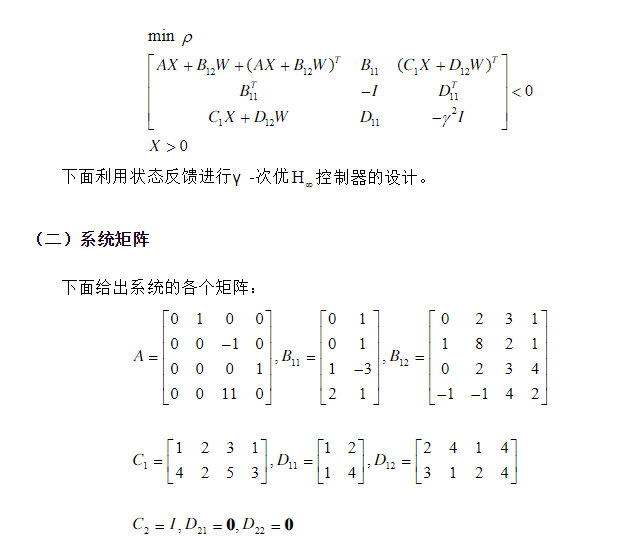
程序：

% 测试--------使用RICCATI进行H infinity的状态反馈设计
%系统参数参见网址：https://wenku.baidu.com/view/c3f834b2ac51f01dc281e53a580216fc710a5358.html?rec_flag=default
clc;clear;close all;
A =[0 1 0 0;
    0 0 -1 0;
    0 0 0 1;
    0 0 11 0];
B1 =[0 1;0 1;1 -3; 2 1];
B2 =[0 2 3 1;
    1 8 2 1;
    0 2 3 4;
    -1 -1 4 2];
%使用网站原来的参数C1的值，求不出riccari的增益K值，为此对其作了些改动
C1=[2 0 0 0;
    0 0.02 0 0;
    0 0 0.04 0;
    0 0 0 0.01;
    0 0 0 0];
D11=[1 2;1 4];
D12 =[0 0 0 0 1]‘;
C2=eye(4);
D21=0;D22=0;
%% 判断系统是否满足基于Riccati方程的假设条件
sys =ss(A,B2,C2,D22);
P0 = pole(sys)
Cc =rank(ctrb(A,B2))
Ob =rank(obsv(A,C2))
S =D12‘*[C1 D12]

%% 利用Riccati方程求解 H infinity 在增益K, A‘*X+X*A+X*(B1*B1‘-B2*B2‘)*X+C‘*C=0
%  A‘*X+X*A-X*[B1 B2]*[-I 0;0 I]*[B1‘;B2‘]*X+C1‘*C1=0
B0 =[B1 B2];
V=[-1,-1,-1,1,1,1];
R=diag(V);
C =C1;
X =care(A,B0,C‘*C,R)
K =-B2‘*X
root =eig(A+K) %判断闭环系统是否稳定；看其特征值是否都有负实部

View Code

仿真结果：

技术图片

ceshi_Hinf_lmi-- discrete time

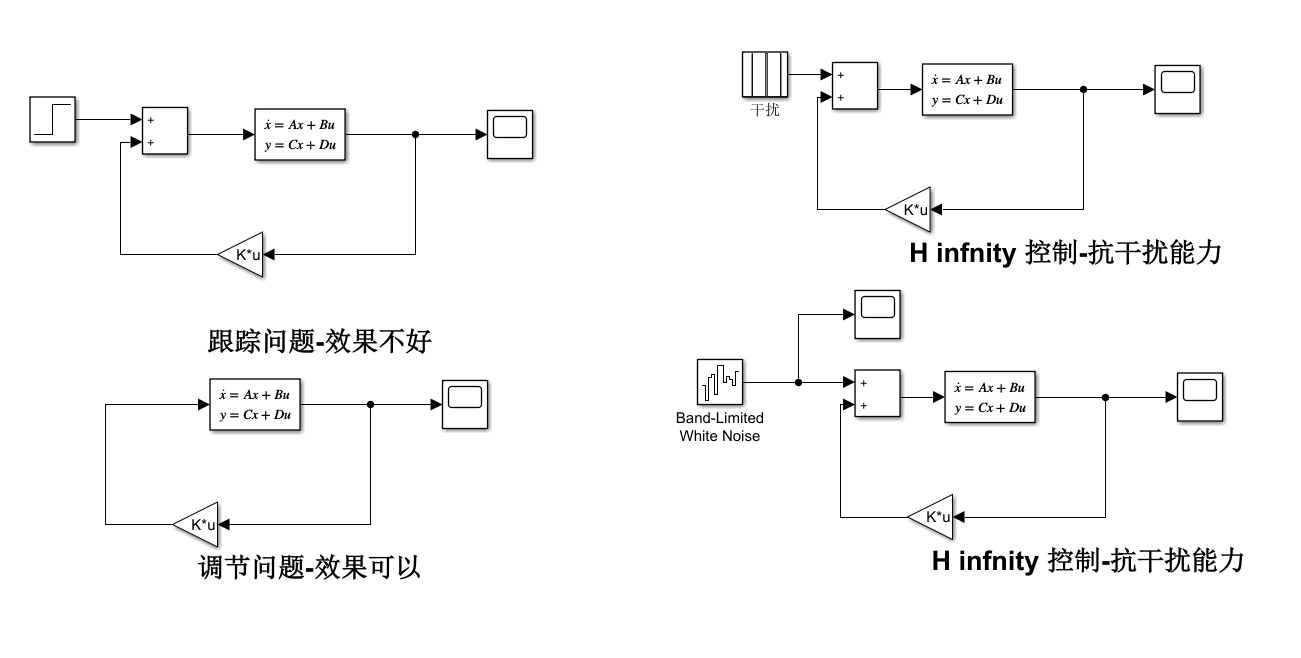
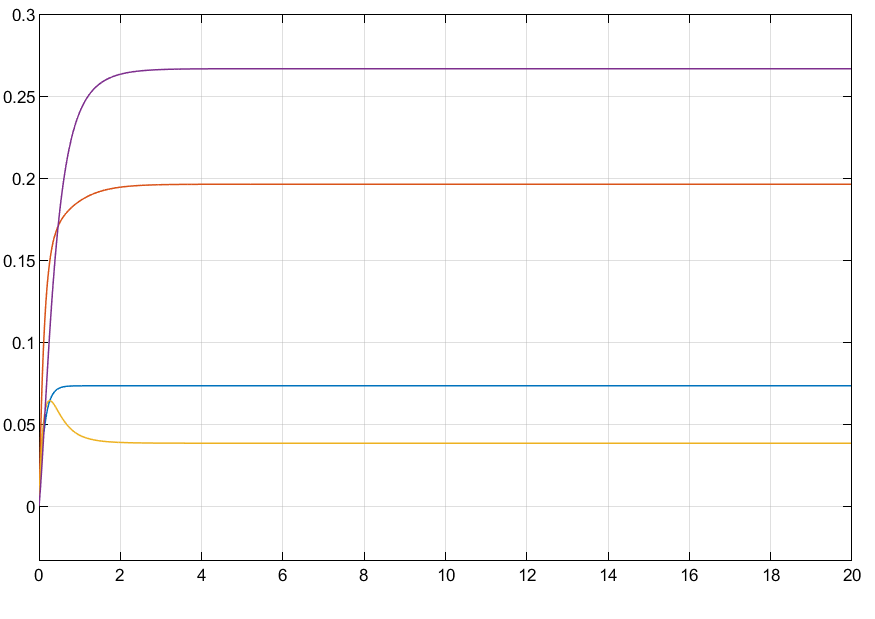
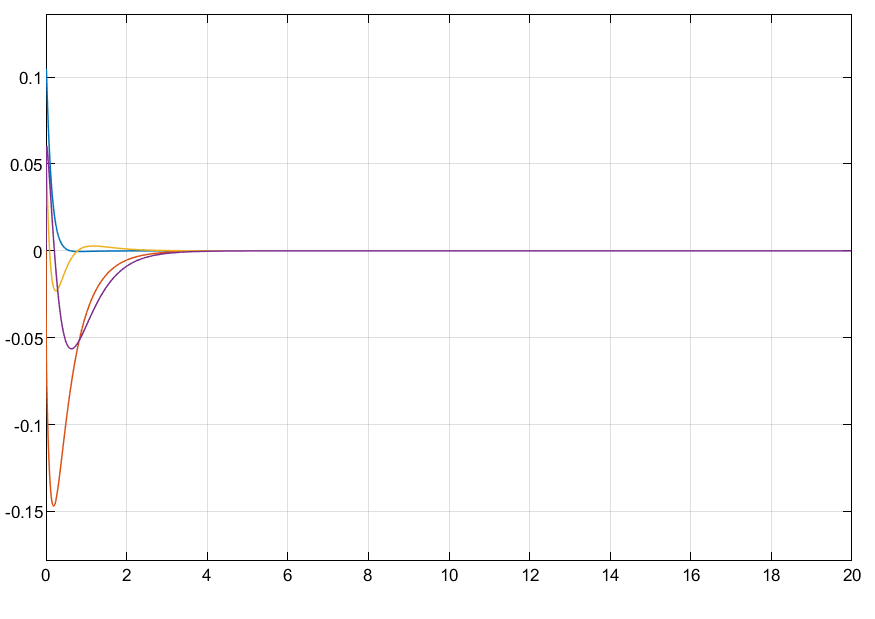
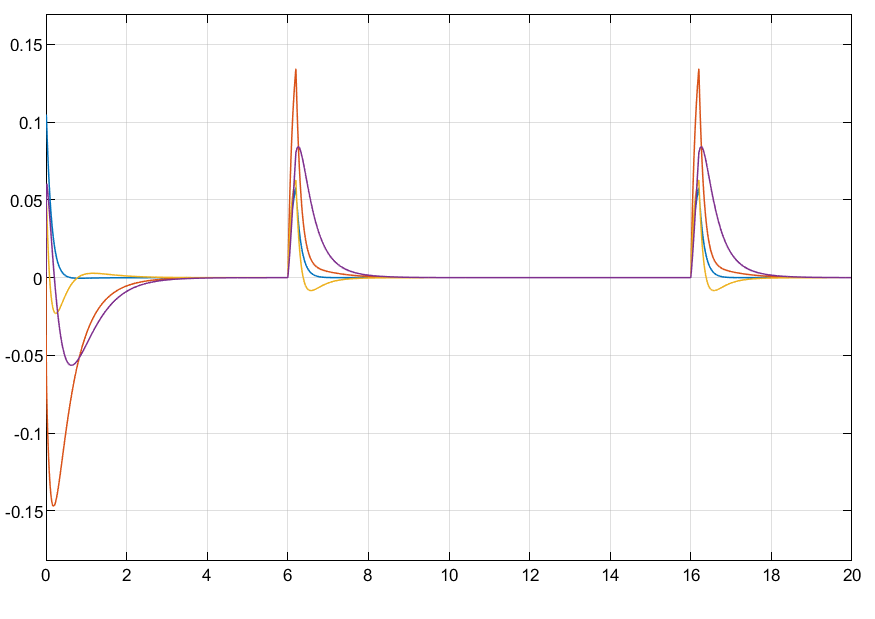
clc;clear; close all;
A  = [2 1 -2;1 -1 -3; 4 0 -1];
B = [1 0;0 3;3 1];
E1 = [1 0.2 -0.5]‘;
C = [2 1 -0.5];
D = [1 1];
E2 = [0.05]

P = 10e+7;
X0 = [8.7047 -6.5321 4.2500;
     -6.5321 8.8601 -4.2821;
     4.2500 -4.2821 5.0227];
W0 = [-5.2786 2.9364 -7.7991;
      -3.4736 -0.8733 6.0925];
W =P*W0; X = X0*P;
K1 =W*inv(X)

Ac =A-B*K1;
Bc = B;
Cc = C;
Dc = D;
sys_cl = ss(Ac,Bc,Cc,Dc);
step(sys_cl)
% figure(1)
% t = 0:0.01:15;
% r =[0.5*ones(size(t));
%     0.5*ones(size(t))];
% [y,t,x]=lsim(sys_cl,r,t);
% plot(t,y)
% 
% 
% K2 = [1.2850 0.5978 -2.0283;
%      -1.4101 -0.7807 1.4861]
% Ac =A-B*K2;
% Bc = B;
% Cc = C;
% Dc = D;
% sys_cl = ss(Ac,Bc,Cc,Dc);
% 
% figure(2)
% t = 0:0.01:15;
% r =[0.5*ones(size(t));
%     0.5*ones(size(t))];
% [y,t,x]=lsim(sys_cl,r,t);
% plot(t,y)

View Code

daolibai_LMI_method----discrete time Hinf state feedback control

% daolibai_LMI_method--Hinf control

clear;clc; 
A = [0 1 0 0;0 -0.0618 -0.7167 0;0 0 0 1;0 0.2684 31.6926 0];
B1 = [0;-2.6838;0;118.6765];
B2 = [0;0.8906;0;-2.6838];
C1 = [0.00001 0 0 0;0 -0.0001 0 0;0 0 -0.01 0;0 0 0 -0.01];
D11 = [0;0;0];
D12 = [0;0;0];
n=length(A); 

 %构建矩阵变量
setlmis([]);
[X,n,sX] = lmivar(1,[4,1]); %4阶的对称满块  
[W,n,sW] = lmivar(2,[1,4]); %4*1的矩阵  

%描述LMI  
lmiterm([1 1 1 W],A);
lmiterm([1 1 1 X],B2,‘s‘);
lmiterm([3 1 1 0],B1);
lmiterm([1 2 1 X],B2,1);
lmiterm([1 2 2 A],D21,2);
lmiterm([1 3 3 0],-1);
lmiterm([2 2 1 W],-1);
lmiterm([-2 2 1 X],1,1);
lmisys = getlmis;
[tmin,xfeas]=feasp(lmisys)
  if(tmin<0)         
         disp(‘Feasible‘);     
      else
         sys=[];         
      return              
   end
X = dec2mat(lmisys,xfeas,X)
W = dec2mat(lmisys,xfeas,W)
K = W*inv(X)

View Code

daolibai_LMI_and_riccati--discrete time Hinf state feedback control

 clear,clc    
 M=1; %小车质量     
 m=0.1; %倒立摆质量      
 L=0.5; %摆的长度     
 g=9.8 ;%重力加速度     
 J=m*L^2/3; %转动惯量          
 k=J*(M+m)+m*M*L^2 ;     
 k1=(M+m)*m*g*L/k ;     
 k2=-m^2*g*L^2/k ;      
 k3=-m*L/k ;     
 k4=( J+m*L^2 ) /k ; %中间变量    

 %------PlantA------------      

 A=[0,0,1,0 ;0,0,0,1 ;k1,0,0,0 ;k2,0,0,0];     
%  B1=[0; 0; 0.09; 0.11 ]; 
 B1=[0;0;0.5;0.5] ;     
 B2=[0; 0; k3; k4];     
 C1=[1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1; ] ; 
 %   C=[1,0,0,0;0,0,0,0] ;     
 N=length(A);     
 D11=0; 
 D12=[0; 0; 0;0; 1]; %状态方程各个矩阵     
 %D12=0;   
 
 % -----直接求出K--------LMI求解
 gamma =4;
 %根据所得的次优gamma重新求解K
%  [X,W]=LMIC(A,B1,B2,C1,D11,D12,gamma,N)
%  K_sub=W*inv(X)
 [X,W,gamma]=LMID(A,B1,B2,C1,D11,D12,N)
 K_opt=W*inv(X)


  
 %   A=[0,1,0,0;10.78,0,0,0;0,0,0,1;-0.98,0,0,0];
 %   B1=[0;0;0.09;0.11];
 %   B2=[0;-1;0;0.5];
 %   N=length(A); 
 %   D12=[0]; 
 %   C=[1,0,0,0]; 
 %   D11=[];   
 %   gamma=4;    
 %% -----LMI求解------------
 %   gamma=2;      
 %   K=LMIC(A,B1,B2,C,D11,D12,gamma,N)  %LMI求解    
 %-------------------  
 %   K=[51.1721, 3.6803, 9.2785, 7.9564];    
 
%% ------PlantB------------ 
 
   A=[0  1       0       0; 
    
     0 -0.0883  0.6293  0; 
     0  0       0       1; 
     0 -0.2357  27.8285 0] ;
     B1=[0 2.3566  0 104.2027]‘; 
     B2=[0 0.8832  0 2.3566]‘;  
      C= [0.064 0   0    0; 
       0     1e-3  0    0; 
       0     0   0.11 0; 
       0     0   0    0.01; 
       0     0   0    0]; 
     D12=[0;0;0;0;1];    

 %% -----Raccati方程求解---可行--------     
%  B=[B1,B2];  
%   C=C1;
%  R=[-1, 0; 0, 1];     
%  X_ric=care(A, B, C‘*C, R)  ;     
%  K_ric=-B2‘*X_ric  %控制器   
 % K=[  112.1078   99.9032 -364.5474  -72.8227]; 
 % X=[0.1253,0.0042,-0.6266,-0.0266; 
 %    0.0042,0.565,0.0156,-0.3558; 
 %    -0.6266,0.0156,3.6427,-0.1747; 
 %    -0.0266,-0.3558,-0.1747,0.5286]; 
 %   W=[0.4583,0.0057,-0.1069,-0.8101]; 
 %   K=W*inv(X)  
 
% function [X,W]=LMIC(A,B1,B2,C1,D11,D12,gamma,N) %次优函数调用
%   %{ 
%   程序功能： 
%    1、利用LMI求解倒立摆 
%    2、状态反馈控制，求控制器 
%    3、参考文献：[1]吕 申,武俊峰.基于 LMI 优化的鲁棒控制器设计[J].工业仪表与自动化装置,2017,3:123-128. 
%    %} 
% 
%    %构建矩阵变量     
%    setlmis([]);     
%    [X,n,Sx]=lmivar(1,[N,1]); %4阶的对称满块    
%    [W,n,Sw]=lmivar(2,[1,N]); %4*1的矩阵          
% 
%     lmiterm([1,1,1,X],A,1,‘s‘);  %AX+(AX)‘     
%     lmiterm([1,1,1,W],B2,1,‘s‘);  %B2*W+(B2*W)‘     
%     lmiterm([1,1,2,0], B1);  %C1*X     
%     lmiterm([1,1,3,X],1,C1‘ ); %D12*W     
%     lmiterm([1,1,4,-W],1,D12‘ ); %W‘*D12‘     
%     lmiterm([1,2,2,0],-gamma^2);%-gamma     
%     lmiterm([1,2,3,0],D11‘); %D12‘     
%     lmiterm([1,3,3,0], -1 ); %-I     
% 
%    %------------------------------------------     
%     lmiterm([-2,1,1,X],1,1); %X正定     
%    %------------------------------------------     
%    lmisys=getlmis ;%获取lmi信息          
%    %求解可行解X,W     
%    [tmin, xfeas]=feasp(lmisys);     
%    if(tmin<0)         
%          disp(‘Feasible‘);     
%       else
%          sys=[];         
%       return              
%    end
%   X=dec2mat(lmisys, xfeas, X);     
%   W=dec2mat(lmisys, xfeas, W);     
% end

View Code

example LMI (yalmip)--discrete time Hinf state feedback control

clc;
clear;
clc;
%% System parameters
A = [0.9641 0.0025 -0.0004 -0.0452;
     0.0044 0.9036 -0.0188 -0.3841;
     0.0096 0.465  0.9435   0.2350;
     0.0005 0.0024 0.0969   1.0120];
Bd1= [0.0440 0.0164;
     0.4898 -0.7249;
     -0.5227 0.4172;
     -0.0266 0.0214];
Bd2 =[0.0440 0.0164;
     0.4898 -0.7249;
     -0.5227 0.4172;
     -0.0266 0.0214];
Cd1 = ones(1,4);
Cd2 = eye(4);
Dd12 = [0.002 0.002];
Dd11 = [1 1];
Dd22 = zeros(4,2);
Ts =0.1;
%% Calculate the H infinity state feedback gain
P = sdpvar(4); 
Z = sdpvar(1); 
Fd = sdpvar(2,4);
gam = sdpvar(1); 
mat1 = [P A*P+Bd2*Fd Bd1 zeros(4,1);
       (A*P+Bd2*Fd)‘ P zeros(4,2) P*Cd1‘-Fd‘*Dd12‘;
       Bd1‘ zeros(2,4) gam*eye(2) Dd11‘;   
       zeros(1,4) (P*Cd1‘-Fd‘*Dd12‘)‘ Dd11 gam*eye(1)];
F = [mat1 >= 0; P>=0];
optimize(F, gam);
Kd = value(Fd)*inv(value(P))
Hinf_norm = (value(gam))
L1 =eig(A-Bd2*Kd)
%% simulation 
% sysd = ss(A,Bd2,Cd2,Dd22);
% feedin = [1 2];
% feedout = [1 2 3 4];
% sys_cl = feedback(sysd,Kd,feedin,feedout)
% 
% Ac = A-Bd2*Kd;
% Bc = Bd2;
% Cc = Cd2;
% Dc = Dd22;
% sys_cl = ss(Ac,Bc,Cc,Dc)
% T = 0:0.1:10;
% step(sys_cl,T)


% clear;
% clc;
A = [0.1 0.2 0.3;
     0.4 0.5 0.6;
     0.7 0.8 0.9];
Bd1 = ones(3,1);
Bd2 = ones(3,1);
Cd1 = ones(1,3);
Dd12 = 1;
Dd11 = 0;
P = sdpvar(3);
Z = sdpvar(1);
Fd = sdpvar(1,3);
gam = sdpvar(1);
mat1 = [P A*P+Bd2*Fd Bd1 zeros(3,1);
       (A*P+Bd2*Fd)‘ P zeros(3,1) P*Cd1‘-Fd‘*Dd12‘;
       Bd1‘ zeros(1,3) gam*eye(1) Dd11‘;
       zeros(1,3) (P*Cd1‘-Fd‘*Dd12‘)‘ Dd11 gam*eye(1)];
F = [mat1 >= 0; P>=0];
optimize(F, gam);
Kd = value(Fd)*inv(value(P))
Hinf_norm = (value(gam))
L2 =eig(A-Bd2*Kd)

View Code

H2 状态反馈控制--模型参数例子来于书本：robust control design _269页--三个例子分开运行

 clc;clear;close all; %文中有三个例子，需要分开运行才可以

%% 模型参数例子来于书本：robust control design _269页
%{
A=[-5 2 -4 ;0 -3 0; 0 7 -1];
B1=[7 -3 1]‘;   B2=[6 8 -5]‘;
C1=[-2 9 4];    C2=[6 3 -1];
D11=[0];     D12=[1];    D21=[2];    D22=[0];

G=ss(A,B2,C2,D22);
P =ltisys(A,[B1 B2],[C1;C2],[D11 D12;D21 D22]);
P1 =pck(A,[B1 B2],[C1;C2],[D11 D12;D21 D22]);
[Aa,Bb,Cc,Dd]=branch(P);
sys=ss(Aa,Bb,Cc,Dd);
po=pole(sys)

nmeas = 1;
ncont = 1;
[K,CL,gamma] = h2syn(sys,nmeas,ncont);

[Ak,Bk,Ck,Dk]=branch(K);
GK=ss(Ak,Bk,Ck,Dk);
K_tf=zpk();
[Knum,Kden]=ss2tf(Ak,Bk,Ck,Dk);
K_tf=tf(Knum,Kden)

% [Aa,Bb,Cc,Dd]=branch(P);
% sys=ss(Aa,Bb,Cc,Dd);
% P_tf=zpk(ss(Aa,Bb,Cc,Dd))
 step(feedback(G*GK,-1),30)
% clsys =slft(P,K);
% splot(clsys,‘st‘)


%}

%{
%% matlab帮助中的h2syn函数的例子
A = [5    6    -6
     6    0     5
    -6    5     4];
B = [0     4     0     0
     1     1    -2    -2
     4     0     0    -3];
C = [-6     0     8
     0     5     0
    -2     1    -4
     4    -6    -5
     0   -15     7];
D = [0     0     0     0
     0     0     0     1
     0     0     0     0
     0     0     3     6
     8     0    -7     0];
P = ss(A,B,C,D);
P1 = pck(A,B,C,D);
pole(P)

nmeas = 2;
ncont = 1;
[K,CL,gamma] = h2syn(P,nmeas,ncont);
pole(CL)
step(CL)
clsys =slft(P,K);
splot(clsys,‘st‘)
[A,B1,B2,C1,C2,D11,D12,D21,D22]=branch(P)
%}




%% 原来旧函数的应用--https://wenku.baidu.com/view/d79bb3cb0722192e44
A =[0     1      0      0; 
    -5000 -100/3 500 100/3;
    0     -1   0         1;
    0    100/3 -4     -60];
B =[0   25/3  0  -1]‘;
C=[0  0  1  0];
D=0;
G =ss(A,B,C,D);
W1=[0 100; 1 1];
W2=1e-5;
W3=[1 0; 0 1000];
T_ss=augtf(G,W1,W2,W3);
[Aa,Bb,Cc,Dd]=branch(T_ss); 
[Aa,Bb,Cc,Dd]=ssdata(T_ss); 

[a,b1,b2,c1,c2,d11,d12,d21,d22]=branch(T_ss);%当使用augtf函数获取增广系统矩阵表达式后，
                                             %可用branch函数获得各个增光系统矩阵的参数
P =rt2smat(T_ss) %变换成系统矩阵P

K_h2=h2lqg(T_ss) %获得H2最优控制器
[AK0,BK0,CK0,DK0]=branch(K_h2);
[AK0,BK0,CK0,DK0]=ssdata(K_h2);%两个函数均可实现这个功能
K_H2_tf=zpk(ss(AK0,BK0,CK0,DK0))
K_Hinf=hinf(T_ss) %获得H00优控制器
[AK1,BK1,CK1,DK1]=branch(K_Hinf);

K_Hinf_tf=zpk(ss(AK1,BK1,CK1,DK1))
[gamma,K_opt]=hinfopt(T_ss); %获得H00最优控制器
[AK2,BK2,CK2,DK2]=branch(K_opt); 
K_opt_tf=zpk(ss(AK2,BK2,CK2,DK2))

% 绘制闭环节约响应下系统的开环bode图
bode(G*K_H2_tf,‘-‘,G*K_Hinf_tf,‘--‘,G*K_opt_tf,‘:‘)

% 闭环阶跃响应曲线
figure(1)
step(feedback(G,K_H2_tf,-1),‘r-‘) 

figure(2)
step(feedback(G*K_H2_tf,1),‘r-‘)
% step(feedback(G*K_H2_tf,1),‘r-‘,feedback(G*K_Hinf_tf,1),‘g--‘,feedback(G*K_opt_tf,1),‘:‘)

%系统矩阵变换函数 -参见：https://wenku.baidu.com/view/d79bb3cb0722192e44
function P =rt2smat(A,B1,B2,C1,C2,D11,D12,D21,D22)
if nargin ==1,
   [A,B1,B2,C1,C2,D11,D12,D21,D22]=branch(A);
end
n =length(A);
P=[A,B1,B2;C1,D11,D12;C2,D21,D22];
P(size(P,1)+1,size(P,2)+1)=-inf;
m=size(P,2);
P(1,m)=n;
end

%}

View Code

H_infinity_looping_shape_control---参考文章：BACHELOR’S FINAL PROJECT（有代码有几种控制方法lqgLQRHOOPID）

clear;clc;
close all;
%% State-space model
A=[-0.38 0.60 -0.36 -9.80;
   -0.98 -10.65 16.74 -0.21;
   0.18 -5.39 -16.55 0;
   0 0 1 0];
B=[-0.36;
   -3.62;
 -141.57;
      0];
C4=[0 0 0 1]; %longitudinal speed u
D=0;
sys=ss(A,B,C4,D);
%% Define system with uncertainties
a11=ureal(‘a11‘,1,‘Percentage‘,10);
a12=ureal(‘a12‘,1,‘Percentage‘,10);
a13=ureal(‘a13‘,1,‘Percentage‘,10);
a14=ureal(‘a14‘,1,‘Percentage‘,10);
a21=ureal(‘a21‘,1,‘Percentage‘,10);
a22=ureal(‘a22‘,1,‘Percentage‘,5);
a23=ureal(‘a23‘,1,‘Percentage‘,5);
a24=ureal(‘a24‘,1,‘Percentage‘,10);
a31=ureal(‘a31‘,1,‘Percentage‘,10);
a32=ureal(‘a32‘,1,‘Percentage‘,5);
a33=ureal(‘a33‘,1,‘Percentage‘,5);
a34=ureal(‘a34‘,1,‘Percentage‘,10);
a41=ureal(‘a41‘,1,‘Percentage‘,10);
a42=ureal(‘a42‘,1,‘Percentage‘,10);
a43=ureal(‘a43‘,1,‘Percentage‘,10);
a44=ureal(‘a44‘,1,‘Percentage‘,10);
uA=[-0.38*a11 0.60*a12 -0.36*a13 -9.80*a14;
  -0.98*a21 -10.65*a22 16.74*a23 -0.21*a24;
   0.18*a31 -5.39*a32 -16.55*a33 0;
   0 0 1*a43 0];
b1=ureal(‘b1‘,1,‘Percentage‘,10);
b2=ureal(‘b2‘,1,‘Percentage‘,5);
b3=ureal(‘b3‘,1,‘Percentage‘,5);
b4=ureal(‘b4‘,1,‘Percentage‘,10);
uB=[-0.36*b1;
    -3.62*b2;
  -141.57*b3;
          0];
usys=ss(uA,uB,C4,D);
%% H-infinity loop shaping
s=tf(‘s‘); %Define s as the Laplace variable
%Singular value diagram to obtain the crossover frequency (Wc)
figure(1)
sigma(sys) %Wc=6.11 rad/s (Value seen on figure 1)
Wc=6.11;
G=Wc/(s); %desired loopshape
% Compute the optimal loop shaping controller K
[K,CL,GAM] = loopsyn(sys,G);
[K.A,K.B,K.C,K.D]=ssdata(K); %得出控制器状态空间表达式参数
%% Closed-loop system
L=K*sys; %Adding disturbance to the system (这句注释的不对)
L_close=feedback(L,1); %Closed-loop
figure(2)
step(L_close);
str=sprintf(‘Step response of the pitch angle \\theta (H-infinity loopshaping)‘);
title(str);
ylabel(‘\theta (rad)‘);
%System information
S_final = stepinfo(L_close)
[y,t]=step(100*L_close);
sserror_final=100-y(end);
%Display gain and phase margins
figure(3)
margin(L_close);
%% Controller simplification
%Hankel singular values of K
figure(4)
hsv = hankelsv(K);
semilogy(hsv,‘*--‘), grid
title(‘Hankel singular values of K (\theta)‘), xlabel(‘Order‘)
%Reduce controller from 7 to 5 states
Kr = reduce(K,5);
order(Kr) %check simplification
%Closed-loop responses comparison (K and Kr)
Lr=Kr*sys;
Lr_close=feedback(Lr,1);
figure(5)
step(L_close,‘b‘,Lr_close,‘r-.‘);
str=sprintf(‘Original and simplified controller (K & Kr) comparison for \\theta‘);
title(str);
ylabel(‘\theta (rad)‘);
legend(‘K‘,‘Kr‘,‘Location‘,‘Southeast‘)
%% Plot step response with uncertainties
uLr=Kr*usys;
uLr_close=feedback(uLr,1); %Closed loop system with uncertainties
figure(6);
step(uLr_close);
str=sprintf(‘Step response of the pitch angle \\theta (H-infinity loopshaping, uncertain plant)‘);
title(str);
ylabel(‘\theta (rad)‘)

View Code

H2_optimal_control_fixed_wing-----基于Ｈ２最优控制的小型无人机飞行姿态控制器设计

clc;clear;close all;

%{
%% State-space system
A=[-0.38   0.60  -0.36  -9.80;
   -0.98  -10.65 16.74 -0.21;
    0.18   -5.39  -16.55  0;
    0       0      1     0];
B2=[-0.36; -3.62; -141.57; 0];
B1 =[0 0.6 0 0.2]‘; %干扰矩阵
C1 =[0.3 0 0 0;     %这个C1矩阵怎样选择
     0 0.4 0 0; 
     0 0 0.1 0;
     0 0 0 0.02]
C2= [0 0 0 1];
D11=zeros(4,1);
D12=[0 0 0 1]‘;
D21=[1];
D22 =[0];
G =ss(A,B2,C2,D22);
P =ltisys(A,[B1 B2],[C1;C2],[D11 D12;D21 D22])
[A1,B1,C1,D1]=branch(P)
nmeas =1; %测量输出个数
ncont =1; %控制输入个数
gmin =0.1; 
gmax=18;
tol =0.0001
% [K,CL,gamma] = hinfsyn(P,nmeas,ncont) %这里为什么不能使用这个函数会出错？
[K,CL,gamma] = hinfsyn(P,nmeas,ncont,gmin,gmax,tol);

%% 画出阶跃响应信号
figure(1)
clsys =slft(P,K); %得到闭环系统
spol(clsys); %该函数返回闭环系统的极点
splot(clsys,‘st‘,1);%画出阶跃响应曲线

% %% 画出控制信号
% figure(2)
% clsys =slft(K,P); %得到闭环系统
% spol(clsys); %该函数返回闭环系统的极点
% splot(clsys,‘st‘);%画出阶跃响应曲线


[Ak,Bk,Ck,Dk]=branch(K)
sys=ss(Ak,Bk,Ck,Dk)
K_tf=zpk(ss(Ak,Bk,Ck,Dk))
[Knum2,Kden2]=ss2tf(Ak,Bk,Ck,Dk)
K_tf1=tf(Knum2,Kden2)
figure(3)
step(feedback(G*K_tf,-1),40,‘-‘)


%% 
G =ss(A,B2,C2,D22);
s=tf(‘s‘)
W1=(100)/(10*s+1);
W2=1e-6;
W3=(10*s)/(s+0.000008);
T_ss=augtf(G,W1,W2,W3);
[Aa,Bb,Cc,Dd]=branch(T_ss); 
[Aa,Bb,Cc,Dd]=ssdata(T_ss); 
K_Hinf=hinf(T_ss) %获得H00优控制器
[AK1,BK1,CK1,DK1]=branch(K_Hinf);

[a,b1,b2,c1,c2,d11,d12,d21,d22]=branch(T_ss)
figure(4)
step(feedback(G,K_Hinf,-1),40,‘-‘)
%}


%% 例子二： 系统参数数据-来自论文：基于Ｈ２最优控制的小型无人机飞行姿态控制器设计
A =[-0.136   11.52  -9.8   0;
    -0.0551 -0.2059   0  0.98;
     0      0      0       1;
    0.026  -0.66   0  -0.5534];
B =[0.34            0.001;
    -0.00167      -0.0063; 
        0               0; 
    -0.000304    -0.00985];
C =[ 0  0  0  1];
% C=eye(4);
D=[0 0];
% D =[0 0 0 0;0 0 0 0]‘;

G =ss(A,B,C,D);
num=[0.008 5]; den =[1 0.0005];  w1 =tf(num,den);
p1=w1;

W1s=w1*eye(4)
W2s=1e-5*eye(2);
W2s=tf(W2s)
p2=W2s;
num1=[8 0.1]; den1 =[0.00001 40];  w2 =tf(num1,den1);
p3=w2;
% num2=[1 1.667e-5]; den2 =[0.00001 40];  w3 =tf(num2,den2);
% W3s=[0   0    0   0;
%     0   w2   0   0;
%     0   0    0   0;
%     0   0    0   w3];
% T_ss=augtf(G,W1s,W2s,W3s);
T_ss=augtf(G,p1,p2,p3);
[Aa,Bb,Cc,Dd]=branch(T_ss); 
[Aa,Bb,Cc,Dd]=ssdata(T_ss)

[a,b1,b2,c1,c2,d11,d12,d21,d22]=branch(T_ss);%当使用augtf函数获取增广系统矩阵表达式后，
                                             %可用branch函数获得各个增光系统矩阵的参数
P =rt2smat(T_ss) %变换成系统矩阵P

K_h2=h2lqg(T_ss) %用H2lqg函数获得H2最优控制器
nmeas = 1;
ncont = 2;
[K,CL,gamma] = h2syn(T_ss,nmeas,ncont) %用H2syn函数获得H2最优控制器
% [] = h2syn(T_ss,nmeas,ncont) %用H2syn函数获得H2最优控制器
[AK0,BK0,CK0,DK0]=branch(K_h2);
[AK0,BK0,CK0,DK0]=ssdata(K_h2);%两个函数均可实现这个功能
K_H2_tf=zpk(ss(AK0,BK0,CK0,DK0))
figure(1)
bode(G*K_H2_tf,‘-‘);
figure(2)
% feedin=[2];
% feedout=[ 4];
% step(feedback(G*K_H2_tf,1,feedin,feedout),‘r-‘)
figure(1)
step(feedback(G*K_H2_tf,1),‘r-‘,6)
figure(2)
step(feedback(G*K,1),‘r-‘,6)
%% 问题 采用H2syn函数时 求出gamma 是无穷代表啥意思

%% 系统进行离散化
Ts=0.1; %采样时间
Gd=c2d(G,Ts,‘z‘) %采用零阶保持器的方法对系统离散化
T_ssd=c2d(T_ss,Ts,‘z‘) %广义系统的离散化
P1 =rt2smat(T_ssd)

[Aad,Bbd,Ccd,Ddd]=branch(T_ss); 
[ad,bd1,bd2,cd1,cd2,dd11,dd12,dd21,dd22]=branch(T_ssd);
% dd11=zeros(4,1);
% Pd =ltisys(ad,[bd1,bd2],[cd1,cd2],[dd11,dd12,dd21,dd22])
Pd =mksys(ad,bd1,bd2,cd1,cd2,dd11,dd12,dd21,dd22,‘tss‘)
Kd_h2=dh2lqg(Pd) %获得离散的H2最优控制器，这里使用的是命令dh2lqg
[AK0d,BK0d,CK0d,DK0d]=branch(Kd_h2);
Kd_h2_tf=zpk(ss(AK0d,BK0d,CK0d,DK0d,Ts)) %将控制器转换成零极点白表达式
figure(3)
bode(Gd*Kd_h2_tf,‘-‘); %画出系统伯德图
figure(4)
step(feedback(Gd*Kd_h2_tf,1),‘r-‘,6)
%}

%系统矩阵变换函数 -参见：https://wenku.baidu.com/view/d79bb3cb0722192e44
function P =rt2smat(A,B1,B2,C1,C2,D11,D12,D21,D22)
if nargin ==1,
   [A,B1,B2,C1,C2,D11,D12,D21,D22]=branch(A);
end
n =length(A);
P=[A,B1,B2;C1,D11,D12;C2,D21,D22];
P(size(P,1)+1,size(P,2)+1)=-inf;
m=size(P,2);
P(1,m)=n;
end

View Code

H infinty 状态反馈-基于Riccati方程方法

%小型固定翼无人机俯仰控制——系统参数参见文章：BACHELOR’S FINAL PROJECT(好done)
% H infinty 状态反馈-基于Riccati方程方法
clear 
close all;
clc
%% State-space system
A=[-0.38   0.60  -0.36  -9.80;
   -0.98  -10.65 16.74 -0.21;
    0.18   -5.39  -16.55  0;
    0       0      1     0];
B2=[-0.36; -3.62; -141.57; 0];
B1 =[0 0.86 0 4.2]‘; %干扰矩阵
C1 =[0.1 0 0 0;     %这个C1矩阵怎样选择
     0 0.04 0 0; 
     0 0 0.02 0;
     0 0 0 0.01;
     0 0 0 0]
C2= [0 0 0 1];% 测量矩阵
% D11 =[0];
D11 =[0;0;0;0;0];
D12 =[0;0;0;0;1];
D21=0;
D22=0;
P =ltisys(A,[B1 B2],[C1;C2],[D11 D12;D21 D22])
%% 判断系统是否满足基于Riccati方程的假设条件
sys =ss(A,B2,C2,D22);
P0 = pole(sys)
Cc =rank(ctrb(A,B2))
Ob =rank(obsv(A,C2))
S =D12‘*[C1 D12]

%% 利用Riccati方程求解H infinity 在增益K, A‘*X+X*A+X*(B1*B1‘-B2*B2‘)*X+C‘*C=0
%  A‘*X+X*A-X*[B1 B2]*[-I 0;0 I]*[B1‘;B2‘]*X+C1‘*C1=0
B =[B1 B2];
R =[-1 0;0 1];
C =C1;
X =care(A,B,C‘*C,R)
K =-B2‘*X
root =eig(A-K) %判断闭环系统是否稳定；看其特征值是否都有负实部

[Aa,Bb,Cc,Dd]=branch(P)
sys=ss(Aa,Bb,Cc,Dd)
P_tf=zpk(ss(Aa,Bb,Cc,Dd))
% 
feedin=[1];
feedout=[1 2 3 4];
step(feedback(sys,K,feedin,feedout,-1));

% clsys1 =slft(P,K);  %得到闭环系统
% spol(clsys1,‘st‘)  %验证闭环系统极点

View Code

H Infinity contrl ---LMI方法（Yalmip 求解）和Riccati 方法

标签：反馈 wro real method ica 技术利用 sigma hsv

原文地址：https://www.cnblogs.com/csymemory/p/14765556.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行