标签：因子   生成   sem   关系   乘法   同余   无限   条件   存在   

代数系统

6-1 代数系统的概念

n元运算

• 定义
• 二元运算的运算表

代数系统的概念

• 代数系统的定义
• 有限代数系统
• 同类型代数系统

6-2二元运算的性质

封闭性

可交换性

幂等性

• 幂等元

有幺元（单位元、恒等元）

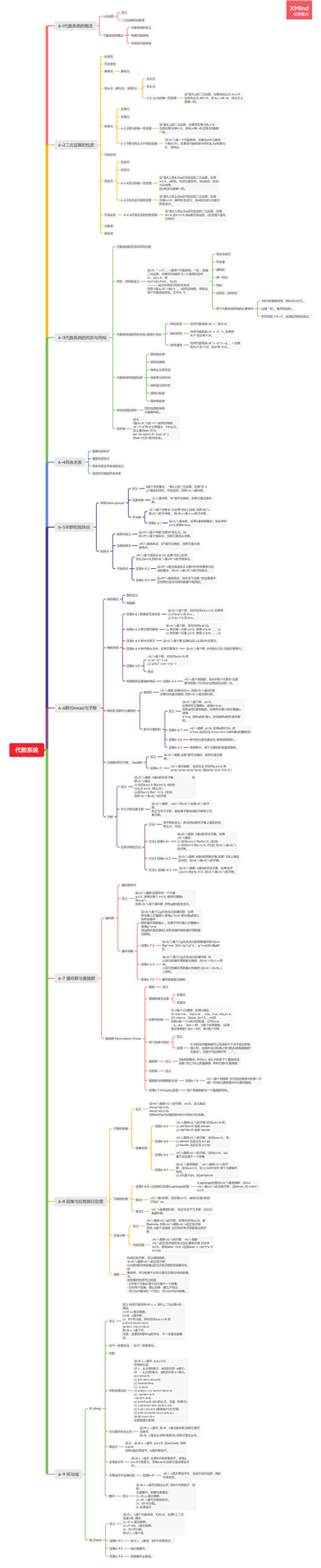
• 左幺元

• 右幺元

• 6-2.1幺元的唯一性定理

  • 设*是X上的二元运算，如果有左幺元 eL∈X， 也有右幺元 eR∈X，则 eL= eR =e，且幺元 e 是唯一的。

有零元

• 左零元

• 右零元

• 6-2.2零元的唯一性定理

  • 设*是X上的二元运算，如果有左零元θL∈X， 也有右零元θR∈X，则θL=θR =θ,且零元θ是唯一的。

• 6-2.3零元和幺元不相同定理

  • 设<A,*>是一个代数系统，且集合A中元素的
    个数大于1。如果该代数系统中存在幺元e和零元θ， 则θ≠e。

可结合性

有逆元

• 左逆元

• 右逆元

• 6-2.4逆元的唯一性定理

  • 设*是X上有幺元e且可结合的二元运算，如果
    x∈X，x的左、右逆元都存在，则x的左、右逆元必相等，
    且x的逆元是唯一的。

• 6-2.5左右逆元相同定理

  • 设*是X上有幺元e且可结合的二元运算，如果
    任意x∈X，都存在左逆元，则x的左逆元也是它的右逆元。

可消去性

• 6-2.6可消去性的判定定理

  • 设*是X上有幺元e且可结合的二元运算，如果a∈X,且a-1∈X.则a是可消去的。(此定理只是充分条件)

分配律

吸收律

6-3代数系统的同态与同构

代数系统的同态和同构问题

同态、同构的定义

• 设<X, * >,<Y, 。>是两个代数系统，* 和 。都是二元运算，如果存在映射f:X->Y,使得对任何x1，x2∈X，有
  f(x1x2)=f(x1) 。f(x2)
  --------此式叫同态(同构)关系式
  则称 f是从<X,>到<Y, 。>的同态映射，简称这两个代数系统同态。记作X∽Y。

  • 同态关系式

  • 同态像

  • 满同态

  • 单一同态

  • 同构

  • 自同态（自同构）

  • 两个代数系统同构的必要条件

    • X和Y的基数相同，即K[X]=K[Y]。
    • 运算 * 和 。是同类型的。
    • 存在双射 f:X->Y，且满足同构关系式。

代数系统间的同构关系≌是等价关系

• ≌有自反性

  • 任何代数系统<X,*> , 有X≌X。

• ≌有对称性

  • 任何代数系统<X,*> <Y, *>, 如果有
    X≌Y 则必有Y≌X。

• ≌有传递性

  • 任何代数系统<X,> <Y,>,<Z, 。> 如果
    有X≌Y 和 Y≌Z，则必有 X≌Z 。

代数系统同构的性质

• 保持结合律
• 保持交换律
• 保持幺元存在性
• 保持零元存在性
• 保持逆元存在性
• 保持分配律
• 保持吸收律

同态性质的保持

• 同态性质的保持
  只是单向的。

同态核

• 定义：
  f是从<X,>到 <Y,>的同态映射，
  (X∽Y),e和 e分别是X、Y中幺元。
  定义集合ker (f)为：
  ker (f)={x|x∈X∧f(x)= e* }
  称ker (f)为 f的同态核。

6-4同余关系

置换性质例子

置换性质定义

同余关系及同余类的定义

由同态可确定同余关系

6-5半群和独异点

半群(Semi-group)

• 定义

  • S是个非空集合， 是S上的二元运算，如果在 S上满足封闭性、可结合性，则称<S,>是半群。

• 交换半群

  • <S,>是半群，如是可交换的，则称它是交换半群。

• 子半群

  • <S,>是个半群,B?S,如果在B上封闭, 则称<B,>是<S,>的子半群。 例<N,+>是<I,+>的子半群。

  • 定理6-5.1

    • 设<S,>是半群，如果S是有限集合，则必存在
      a∈S,使得aa=a。

独异点

• 独异点定义

  • 设<M,>是个半群,如果对有幺元。则
    称<M,*>是个独异点，也称它是含幺半群。

• 交换独异点

  • <M,>是独异点，如是可交换的，则称它是交换独异点。

• 子独异点

  • <M,>是个独异点,B?M, 如果在B上封闭，
    且幺元e∈B,则称<B,>是<M,>的子独异点。

  • 定理6-5.2

    • 设<M,>是交换独异点,A是M中所有幂等元构
      成的集合，则<A,>是<M,*>的子独异点。

  • 定理6-5.3

    • 设<M,*>是独异点，则在关于运算 *的运算表中任何两行或任何两列都是不相同的。

6-6群(Group)与子群

群的概念

• 群的定义
• 有限群

群的性质

• 定理6-6.1 群满足可消去性

  • 设<G,>是个群，则对任何a,b,c∈G, 如果有
    ⑴ ab=ac 则 b=c 。
    ⑵ ba= c*a 则 b=c 。

• 定理6-6.2 群方程可解性

  • 设<G,>是个群，则对任何a,b∈G,
    ⑴ 存在唯一元素 x∈G, 使得 ax=b ……..⑴
    ⑵ 存在唯一元素 y∈G, 使得 y*a=b ……..⑵

• 定理6-6.3 群中无零元

  • 设<G,*>是个群,如果K[G] ≥2,则G中无零元.

• 定理6-6.4 群中除幺元外，无其它幂等元

  • 设<G,*>是个群 ,G中除幺元外,无其它幂等元。

• 定理6-6.5

  • <G,>是个群，对任何a,b∈G,有
    ⑴ (a^-1)-1 =a
    ⑵ (ab)^-1=b-1*a^-1
  • 推论

• 有限群的运算表的特征

  • 定理6-6.6

    • <G,>是个有限群，则G中每个元素在运算
      表中的每一行(列)必出现且仅出现一次。

群的阶与群中元素的阶

• 群的阶

  • <G,>是群,如果K[G]=n, 则称<G,>是n阶群,
    如果K[G]是无限的, 则称<G,*>是无限阶群。

• 群中元素的阶

  • 定义

    • 设<G,*>是个群，a∈G，
      如果存在正整数k，使得a^k=e,
      则称a的阶是有限的。如果存在最小的正整数n，使得
      a^n=e, 则称a的阶是n。否则就称a的阶是无限的。

  • 定理6-6.7

    • <G,*>是群, a∈G, 如果a的阶为n ,则
      a^k=e 当且仅当 k=mn (m∈I)(即k是n的整数倍)

  • 定理6-6.8

    • 群中的元素与其逆元 具有相同的阶。

  • 定理6-6.9

    • 有限群中，每个元素的阶都是有限的。

交换群(阿贝尔群 、Abel群)

• 定义

  • 设<G,>是群,运算是可交换的，则称它是交换群。

• 定理6-7.1

  • <G,>是交换群，当且仅当 对任何a,b∈G 有
    (ab)(ab)=(aa)(bb) (即(ab)^2=a2*b^2 )

子群

• 定义

  • 设<G,>是群, S是G的非空子集， 如果<S,>满足：
    ⑴ 任何a,b∈S 有ab∈S, (封闭)
    ⑵幺元 e∈S, (有幺元)
    ⑶任何a∈S 有a^-1∈S, (可逆)
    则称<S,>是<G,*>的子群

• 平凡子群与真子群

  • 设<G,>是群，<{e},>和<G,>也是<G,>的子群。
    称之为平凡子群。其余真子集构成的子群称之为真子群。

• 证明子群的方法

  • 方法1

    • 用子群的定义，即证明运算在子集上满足封闭、
      有幺元、可逆。

  • 方法2.定理6-8.1

    • 设<G,>是群, S是G的非空子集，如果
      <S,>满足：
      ⑴ 任何a,b∈S 有ab∈S, (封闭)
      ⑵ 任何a∈S 有a-1∈S, (可逆) 则<S,>是<G,*>的子群。

  • 方法3.定理6-8.2

    • 设<G,>是群, B是G的有限子集,如果 在B上满足封闭性，则<B,>是<G,>的子群。

  • 方法4. 定理6-8.3

    • 设<G,>是群, S是G的非空子集，如果任何
      a,b∈S 有ab-1∈S, 则<S,>是<G,>的子群。

6-7 循环群与置换群

循环群

• 循环群例子

• 定义

  • 设<G,>是群,如果存在一个元素
    g∈G, 使得对每个 x∈G, 都存在整数i,
    有x=g^i, 则称<G,>是个循环群. 并称g是G的生成元。

• 循环周期

  • 设<G,*>是个以g为生成元的循环群，如果
    存在最小正整数m,使得g^m=e (即m是g的阶)，则称该循环
    群的循环周期是m 。如果不存在最小正整数m, 使得g^m=e
    (即g的阶是无限的),则称该循环群的循环周期是无限的。

  • 定理6-7.2

    • 设<G,*>是个以g为生成元的有限循环群,|G|=n
      则g^n=e, 及G= {g^1,g2,.., g^n=e}且n是g的阶。

  • 定理6-6.2

    • 设<G,>是个以g为生成元的循环群, 则
      ⑴若它的循环周期是无限的，则<G,>与<I,+>同构。
      ⑵若它的循环周期是k(有限的),则<G,*>与<N?,+?>同构。

  • 定理6-7.3

    • 循环群都是交换群。

置换群 Permutation Group

• 置换

  • 定义

• 置换的复合运算

  • 左复合
  • 右复合

• 轮换与对换

  • 令 σ是个n元置换，如果σ满足：
    (1) σ(a?)=a?，σ(a?)=a? … σ(a???)=a? σ(a?)= a?
    (2) σ(a)=a，当a≠a? (k=1,2,…,m)时
    则称σ是一个m轮次的轮换，记作(a?a? …a???a?)。 当m＝1时，σ是个恒等置换。(实际是恒等映射) 当m＝2时，称σ是个对换

• 两个轮换不相交

  • 定义

  • 定理

    • S?中的任何置换都可以写成若干个互不相交的轮换之积。这里所说对轮换之积(乘法)就是置换的“左复合”。但是不写运算符号“ 。” 。

• 置换群

  • 定义

    • S是有限集合, 令|S|=n, 由S?中的若干个置换构成
      的群, 称之为S上的置换群. 并称它是n元置换群。

• 对称群

  • 定义

• 置换群与有限群的关系

  • 定理6-7.4

    • <G,*>是个有限群, 则它的运算表中的每一行
      (每一列)的元素都是G中元素的置换。

• 定理6-7.5(Cayley定理)

  • 每个有限群都与一个置换群同构。

6-8 陪集与拉格朗日定理

子群的陪集

• 定义

  • 设<H,>是群<G,>的子群，a∈G，定义集合:
    aH={ah|h∈H}
    Ha={ha|h∈H}
    则称aH(Ha)为a确定的H在G中的左(右)陪集。

• 陪集性质

  • 定理6-8.4

    • <H,>是群<G,>的子群,任何a,b∈G,有
      ⑴ aH∩bH=Φ 或者 aH=bH
      ⑵ Ha∩Hb=Φ 或者 Ha=Hb

  • 定理6-8.5

    • <H,>是群<G,>的子群，任何a,b∈G，有
      ⑴ aH=bH 当且仅当 b∈aH
      ⑵ Ha=Hb 当且仅当 b∈Ha

  • 定理6-8.6

    • <H,>是群<G,>的子群，任何a∈G，a必
      属于且仅属于一个陪集

  • 定理6-8.7

    • 设<G,>是有限群， <H,>是群<G,*>的子
      群，任何a,b∈G，则 ⑴ bH中任何 两个元素都不相同。
      ⑵ a不属于bH，则aH∩bH=Φ

子群的阶数

• 定理6-8.8--拉格朗日定理(Lagrange定理)

  • (Lagrange定理)设<G,>是有限群，|G|=n,
    <H,>是<G,*>的任意子群，且|H|=m, 则 n=km (k∈I)

• 推论1

  • <G,*>是n阶群，则任意a∈G，a的阶必是n的因子且a? =e。

• 推论2

  • <G, *>是素数阶群， 则它无非平凡子群，且它必是循环群。

正规子群

• 定义

  • <H,>是群<G,>的子群，如果对任何a∈G，都
    有aH=Ha, 则称<H,>是群<G,>的正规子群.
    显然, G是个交换群, 则它的所有子群都是正规子群.

• 判定定理

  • <H,>是群<G,>的子群，<H,>是群
    <G,>的正规子群的充分且必要条件是 对任何a∈G，都有aHa^-1?H. (这里aHa^-1 ={aha-1| h∈H})

商群

• 利用正规子群，可以得到商群。
  令<H,>是群<G,>的正规子群，
  G/H是H的所有陪集(因为正规子群的左陪集与右陪
  集相等，所以陪集不必区分是左还是右)构成的集合。
  由陪集的性质可以知道：
  ? G中每个元素必属于且只属于一个陪集；
  ? 任何两个陪集，要么相等，要么不相交；
  ? 所以G/H是G的一个划分。所以G/H也叫商集。

6-9 环与域

环 (Ring)

• 定义

  • 定义:给定代数系统<R,+,·>, 若R上二元运算+和 · 满足:
    ⑴<R,+>是交换群。
    ⑵<R, ·>是半群。
    ⑶ · 对+可分配。即对任何a,b,c∈R,有
    a·(b+c)=(a·b)+(a·c)
    (a+b)·c =(a·c)+(b·c)
    称<R,+,·>是个环。
    注意：这里的R是Ring的字头，不一定是实数集合。

• 也不一定是加法；· 也不一定是乘法。

• 判断

• 环的运算法则

  • 设<R,+,·>是环, a,b,c∈R,
    符号的约定：
    对 +：幺元用0表示，a的逆元用 -a表示；
    对 · ：幺元用1表示，a的逆元用 a-1表示。
    a+(-b)=a-b
    ⑴ a+(-a)=(-a)+a=0
    ⑵ 0+a=a+0=a
    ⑶ -(-a)=a
    ⑷ a+b=c <=> a=c+(-b)=c-b
    ⑸ -(a+b)=-a-b
    -(a-b)=-a+b
    ⑹ a·0=0·a=0 (对+的幺元，恰是 · 的零元)
    ⑺ (-a)·b=a·(-b)=-(a·b)=-a·b
    ⑻ (-a)·(-b)=a·b (直接由(7)式可得)
    ⑼ a·(b-c)=(a·b)-(a·c)=a·b-a·c
    (a-b)·c=a·c-b·c
    实质就是分配律。

• 可交换环和含幺环

  • 设<R,+,·>是环, 若<R, ·>是交换半群,则称它是可交换环。
    若<R, ·>是含幺半群(独异点),则称它是含幺环。

• 零因子

  • 定义：设<R,+,·>是环, a,b∈R, 且a≠0,b≠0, 但有a·b=0,
    则称a是左零因子，b是右零因子。

• 含零因子环

  • 设<R,+,·>是环, 如果R中含有零因子，即有a,b∈R不是零元，而有a·b=0,则称它是含零因子环。

• 无零因子环及其判定

  • 定理6-9.1

    • <R,+,·>是无零因子环，当且仅当对运算 · 满足
      可消去性。

• 整环

  • 定义

    • 设<R,+,·>是可交换含幺环, 若R中无零因子，则称
      它是整环。即整环是满足：
      ⑴ <R,+>是交换群。
      ⑵ <R, ·>是可交换独异点。
      ⑶ · 对+可分配。
      ⑷ 无零因子

域 (Field)

• 定义

  • 设<F,+, ·>是个代数系统，K[F]≥2，如果F上二元
    运算+和 ·满足：
    ⑴ <F,+>是交换群。
    ⑵ <F-{0}, ·>是交换群。
    ⑶ · 对+可分配。
    称<F,+,·>是个域

• 定理6-9.2

  • 设<F,+, ·>是域，则F中无零因子。

• 定理6-9.3

  • 域必是整环。

• 定理6-9.4

  • 有限整环必是域。

代数系统

标签：因子   生成   sem   关系   乘法   同余   无限   条件   存在   

原文地址：https://www.cnblogs.com/Adalight/p/14805025.html