标签:eof color ati 网络流 val for cst 技术 ==
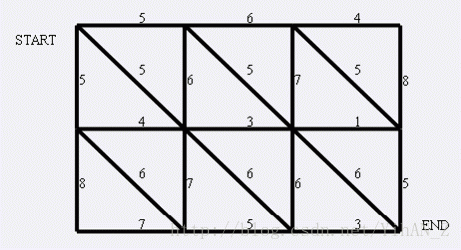
题目大意:给出一张左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
n,m<=1000
求最小割.
数据太大,网络流会很卡(不太清楚用一些玄学的底层优化能不能卡过去)
这时我们需要用到非常神奇的结论:最小割转最短路
根据欧拉公式,如果一个连通的平面图1有n个点,m条边和f个面,那么f=m-n+2(在上图中 n=12,m=23,f=13)
现在,把面与点反过来,即面作为点,点作为面,那么对于每条边
1.边只属于一个面,给对应点连一个自环;
2.边两侧各有一个面,给对应点之间连一条无向边
这样,我们就做了一个原图的对偶图2,有什么用呢?
对偶图的路径对应原图的割
那么平面图的最小割=其对偶图的最短路
在本题中,即靠上、右面的边与起点连边,靠下、左面的边与终点连边,其他的对应连边即可,点均以左上角为准,0/1分别代表一个正方形中的上下两个面(三角形)。
具体可参照下图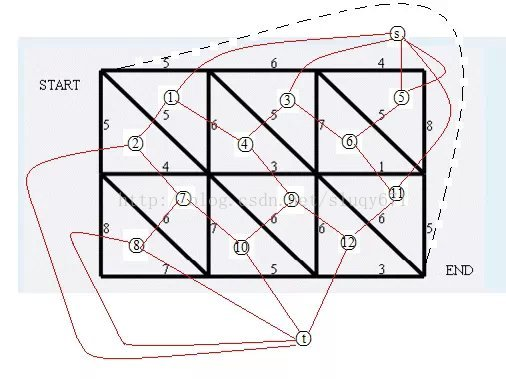
#include <cstdio> #include <cstring> #include <queue> #include <algorithm> #include<bits/stdc++.h> #define N 2000005 using namespace std; int n,m,S,T,top=-1,fir[N],num[1005][1005][2]; struct Edge { int to,nxt,val; }e[N*4]; void Add_Edge(int from,int to,int val) { e[++top].to=to; e[top].val=val; e[top].nxt=fir[from]; fir[from]=top; e[++top].to=from; e[top].val=val; e[top].nxt=fir[to]; fir[to]=top; return ; } struct Node { int ord,val; Node(int x=0,int y=0):ord(x),val(y){} bool operator < (const Node& rhs) const { return val>rhs.val; } }; int Dijsktra() { static priority_queue<Node> q; static bool k[N]; static int dist[N]; memset(dist,0x7f,sizeof dist); dist[S]=0; q.push(Node(S,0)); while(!q.empty()) { Node tmp=q.top(); q.pop(); int x=tmp.ord,v=tmp.val; if(k[x]) continue; k[x]=true; for(int i=fir[x];i!=-1;i=e[i].nxt) { int to=e[i].to; if(dist[to]<=dist[x]+e[i].val) continue; dist[to]=dist[x]+e[i].val; q.push(Node(to,dist[to])); } } return dist[T]; } int main(){ memset(fir,-1,sizeof fir); scanf("%d%d",&n,&m); if(n==1 || m==1) { int ans=2147483647; n=max(n,m); for(int i=1;i<=n;i++) { int x; scanf("%d",&x); ans=min(ans,x); } printf("%d\n",ans); return 0; } T=1; for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) num[i][j][0]=((m-1)*(i-1)+j-1)*2+2 , num[i][j][1]=num[i][j][0]+1; for(int i=1;i<=n;i++){ for(int j=1;j<m;j++){ int x; cin>>x; if(i==1){ Add_Edge(num[i][j][1],S,x); } else if(i==n){ Add_Edge(num[i-1][j][0],T,x); } else{ Add_Edge(num[i][j][1],num[i-1][j][0],x); } } } for(int i=1;i<n;i++){ for(int j=1;j<=m;j++){ int x; cin>>x; if(j==1){ Add_Edge(num[i][j][0],T,x); } else if(j==m){ Add_Edge(num[i][j-1][1],S,x); } else{ Add_Edge(num[i][j-1][1],num[i][j][0],x); } } } for(int i=1;i<n;i++){ for(int j=1;j<m;j++){ int x; cin>>x; Add_Edge(num[i][j][1],num[i][j][0],x); } } cout<<Dijsktra()<<endl; }
标签:eof color ati 网络流 val for cst 技术 ==
原文地址:https://www.cnblogs.com/LH2000/p/14823773.html