标签：ble   努力   info   clu   相关   lan   can   show   type   

三元环问题

解题思路： 度 = 入度 + 出度

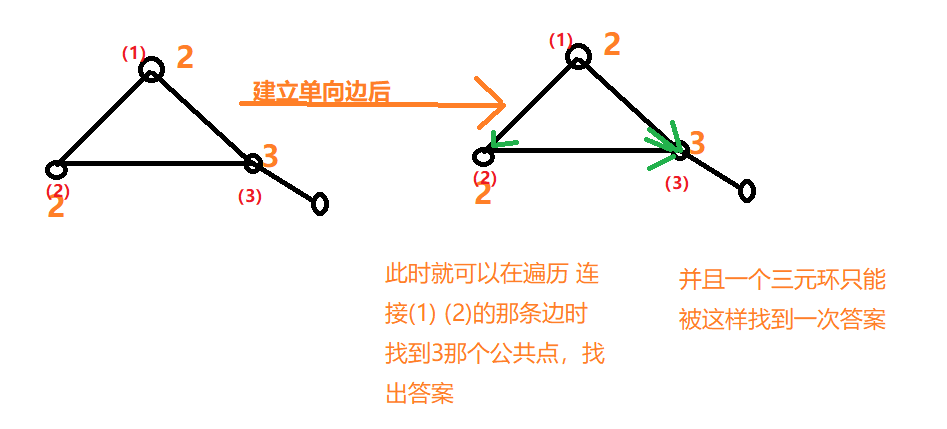
根据 1、度小的连向度大的 2、若度相同，则编号小的连向编号大的

把所有的边建立成有向边（防止后面重复的统计三元环）

然后for循环遍历所有的边 判断所有的边的两端点，判断两个端点有没有连接，如果有连接，那么就ans++。

代码：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 3e5+5,M=6e5+6;
int h[N],ne[M],e[M],idx;

void add(int a,int b){
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;	
}
int du[N];
int vis[N];
int X[M],Y[M];
//记录输入的一条边上的两个点 
typedef long long ll;
 
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=0;i<m;i++){
		scanf("%d%d",&X[i],&Y[i]);
		du[X[i]]++;
		du[Y[i]]++;		
	}
	//建立有向边的要求： 
	//数小的往度数大的走
	//度数相同则按编号(值)小到大走
	memset(h,-1,sizeof h); 
	for(int i=0;i<m;i++){
	//在此，将所有的边建立成有向边的形式 
		if(du[X[i]]<du[Y[i]]){
			add(X[i],Y[i]);
		}else if(du[Y[i]]<du[X[i]]){
			add(Y[i],X[i]);
		}else{//编号 
			if(X[i]<Y[i]){
				add(X[i],Y[i]);
			} else{
				add(Y[i],X[i]);
			}
		}
	}
	ll ans=0;
	for(int i=0;i<m;i++){
		int u=X[i],v=Y[i];//此时直线两端的两个点
		for(int j=h[u];j!=-1;j=ne[j]){
			int x=e[j];//u所连接的点进行标记 
			vis[x]=i+1;
		} 
		for(int j=h[v];j!=-1;j=ne[j]){
			int x=e[j];//v所连接的点 
			if(vis[x]){//如果发现这个点被标记过了，则表示形成了三元环 
				ans++;
			}
		}
	}
	cout<<ans<<endl;
	return 0;
} 

相关题目：

Counting Stars（2017广西邀请赛）

题目链接：Problem - 6184 (hdu.edu.cn)

解题思路：

记录每条边可以连接成的三元环的个数，如果个数小于等于1，那么可以形成的A-structure数量一定是0。

如果>=2,则这个边（作为中间那条边），可以形成的A-structure数量就是C( cnt[i], 2)。 所有边C( cnt[i], 2)的加和就是答案。

AC代码：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 3e5+5,M=6e5+6;
typedef long long ll;
typedef pair<ll,ll> PII;
ll h[N],ne[M],idx,cnt[M];
PII e[M];

void add(ll a,ll b){
	e[idx]={b,idx},ne[idx]=h[a],h[a]=idx++;	
}

ll du[N];
ll vis[N];
ll X[M],Y[M];
//记录输入的一条边上的两个点 
ll now[N];
int main(){
	ll n,m;
	while(scanf("%lld%lld",&n,&m)!=EOF){
		memset(cnt,0,sizeof cnt);
		memset(du,0,sizeof du);
		memset(vis,0,sizeof vis);
		idx=0;
		for(ll i=0;i<m;i++){
			scanf("%lld%lld",&X[i],&Y[i]);
			du[X[i]]++;
			du[Y[i]]++;		
		}
		//建立有向边的要求： 
		//数小的往度数大的走
		//度数相同则按编号(值)小到大走
		memset(h,-1,sizeof h); 
		for(ll i=0;i<m;i++){
		//在此，将所有的边建立成有向边的形式 
			if(du[X[i]]<du[Y[i]]){
				add(X[i],Y[i]);
			}else if(du[Y[i]]<du[X[i]]){
				add(Y[i],X[i]);
			}else{//编号 
				if(X[i]<Y[i]){
					add(X[i],Y[i]);
				} else{
					add(Y[i],X[i]);
				}
			}
		}
		
		for(ll i=0;i<m;i++){
			ll u=X[i],v=Y[i];//此时直线两端的两个点
			for(ll j=h[u];j!=-1;j=ne[j]){
				ll x=e[j].first;//u所连接的点进行标记 
				vis[x]=i+1;
				now[x]=j;
			} 
			for(ll j=h[v];j!=-1;j=ne[j]){
				ll x=e[j].first;//v所连接的点 
				if(vis[x]==i+1){//如果发现这个点被标记过了，则表示形成了三元环 
					cnt[i]++;
					cnt[now[x]]++;
					cnt[j]++;
				}
			}
		}
		ll ans=0;
		for(ll i=0;i<m;i++){
			ans+=(cnt[i]*(cnt[i]-1))/2;
		}
		cout<<ans<<endl;
	}

	return 0;
} 

祝各位努力早日成为图论dalao！

三元环问题

标签：ble   努力   info   clu   相关   lan   can   show   type   

原文地址：https://www.cnblogs.com/AC673523745/p/14827536.html