标签:lazy scan loading not strong 数据结构 img image 二维数组
·一、实验目的
实验目的:练习多维数组的用法
·二、实验原理
鞍点(Saddle point)在微分方程中,沿着某一方向是稳定的,另一条方向是不稳定的奇点,叫做鞍点。在泛函中,既不是极大值点也不是极小值点的临界点,叫做鞍点。在矩阵中,一个数在所在行中是最大值,在所在列中是最小值,则被称为鞍点。在物理上要广泛一些,指在一个方向是极大值,另一个方向是极小值的点。
找出一个二维数组中的鞍点:在该位置上的元素在该行上最大、在该列上最小。有的数组有鞍点,有的没有。
·三、主要数据结构和算法
算法分析
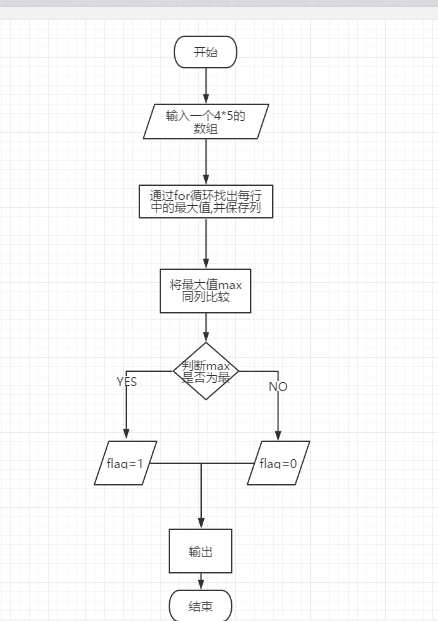
·四、实验结果及分析
测试结果截图
(1)第一组测试数据及结果截图
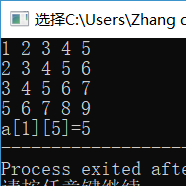
(2)第二组测试数据及结果截图
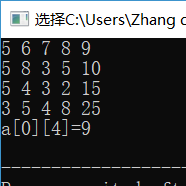
(3)第三组测试数据及结果截图
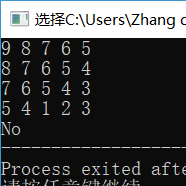
·五、心得体会
1 理解鞍点的特点,根据其设计算法;
2 分清行号i和列号j所对应的数值含义
3 设立标记,flag,类似于bool类型
·六、源文件
#include <stdio.h> int main() { int i, j, k, a[4][5], max, maxj, flag; for (i = 0; i < 4; i++) //输入数组 for (j = 0; j < 5; j++) scanf("%d", &a[i][j]); for (i = 0; i < 4; i++) { max = a[i][0]; //开始时假设a[i][0]最大 maxj = 0; //将列号赋给maxj for(j=0;j<5;j++) if (a[i][j] > max) { max = a[i][j]; //将本行的最大数存放在max中 maxj = j; //将最大数所在的列号存赋值给maxj } flag = 1; //以flag为1表示鞍点 for(k=0;k<4;k++) if (max > a[k][maxj]) //将最大数和其同列元素相比 { flag = 0; //如果max不是同列最小,表示不是鞍点,令flag=0; continue; } if(flag) //如果flag为1表示鞍点 { printf("a[%d][%d]=%d\n", i, maxj, max);//输出鞍点的值和所在行列号 break; } } if (!flag) //如果flag为0表示鞍点不存在 printf("Not found.\n"); return 0; }
标签:lazy scan loading not strong 数据结构 img image 二维数组
原文地址:https://www.cnblogs.com/zhang-a-d/p/14826791.html