标签:open namespace stl nbsp ide loading 现在 spl 技术
对于二叉搜索树,我们规定任一结点的左子树仅包含严格小于该结点的键值,而其右子树包含大于或等于该结点的键值。如果我们交换每个节点的左子树和右子树,得到的树叫做镜像二叉搜索树。
现在我们给出一个整数键值序列,请编写程序判断该序列是否为某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列,如果是,则输出对应二叉树的后序遍历序列。
输入的第一行包含一个正整数N(≤1000),第二行包含N个整数,为给出的整数键值序列,数字间以空格分隔。
输出的第一行首先给出判断结果,如果输入的序列是某棵二叉搜索树或某镜像二叉搜索树的前序遍历序列,则输出 YES ,否侧输出 NO 。如果判断结果是 YES ,下一行输出对应二叉树的后序遍历序列。数字间以空格分隔,但行尾不能有多余的空格。
7 8 6 5 7 10 8 11
YES 5 7 6 8 11 10 8
7 8 6 8 5 10 9 11
NO
这道题真的很简单啊!但不知道为什么我用了3个多小时才写出来,昨天的状态是真的差啊。特意来记录一下。
题目还是很直白的,先说一下大体的思路和代码框架。
现在先说一下如何判断这树搜索树还是镜面搜索树,也就是这两种搜索树有什么区别。
由于我们得到的是这颗搜索树的先序遍历的结果,所以这个序列应该满足这个特征:序列的第一个元素是这颗搜索树的根节点,然后序列接下来的某部分是这颗搜索树的左子树,序列剩下的部分是这颗搜索树的右子树。入如图:
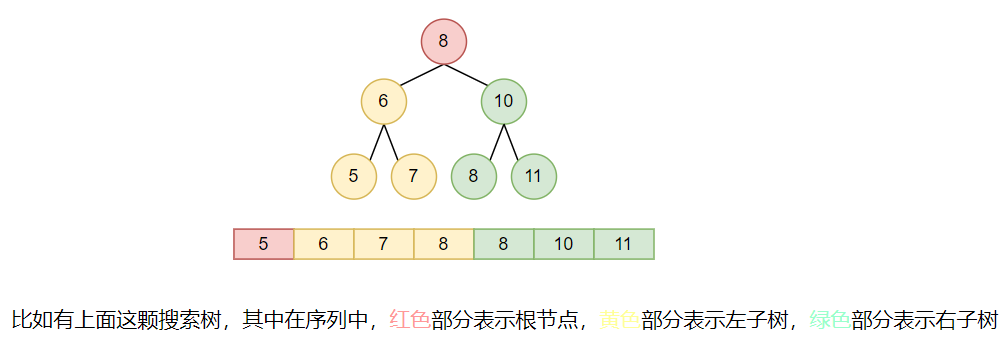
当然,这并不是搜索树特有的特性,所有的二叉树通过先序遍历得到的先序序列都符合上述所说的特征。
而区分这颗树是搜索树还是普通的二叉树的关键在于,搜索树的左子树部分都比根节点要小,而右子树都比根节点要大或相等(这里的说法不太严谨,其实我想表述的意思是,左子树每个节点所存放的值都比根节点存放的值要小,右子树同理。为了方便表述,下面我都用这种方式来表述这种关系)。而普通的二叉树则不然。所以这就是用来区分搜索树和普通二叉树的方法。
那么镜像搜索树呢?按照定义,其实它和搜索树差不多,不同的地方就在于,镜像搜索树的左子树部分都比根节点要大或相等,而右子树都比根节点要小。
所以判断这是颗树是什么树的方法可以是:先判断一下序列的第2个元素和第1个元素的大小关系。然后以序列的第1个元素为标杆:
接下来我们用一个指针,从第2个元素开始,如果指针所指向的元素比序列第1个元素要小,那么指针向后移动一个位置。如此循环,直到某个元素比第1个元素大或相等就停下来,退出循环。
这说明我们已经找完左子树了,现在指针停在右子树开始的位置。我们从这个位置继续。
我们知道对于搜索树,右子树都是比根节点要大或相等,所以只有当指针所指的那个元素不小于序列第1个元素,才向后移动一个位置。其中,如果发现某个元素小于序列第1个元素,就退出循环。
然后看看指针的位置,如果指针指向序列的最后一个位置的下一个位置(也就是没有元素的位置),那么就说明这是一颗搜索树,满足左子树都比根节点小,右子树都比根节点大或相等的特性。否则,就说明这不是一颗搜索树,而是普通的二叉树。
同样的方法,用一个指针,从第2个元素开始,如果指针所指向的元素比序列第1个元素要大或相等,那么指针向后移动一个位置。如此循环,直到某个元素比第1个元素小就停下来,退出循环。
这说明我们已经找完左子树了,现在指针停在右子树开始的位置。我们从这个位置继续。
我们知道对于镜像搜索树, 右子树都是比根节点要小,所以只有当指针所指的那个元素小于序列第1个元素,才向后移动一个位置。其中,如果发现某个元素大于或等于序列第1个元素,就退出循环。
然后看看指针的位置,如果指针指向序列的最后一个位置的下一个位置(也就是没有元素的位置),那么就说明这是一颗镜像搜索树,满足左子树都比根节点大或相等,右子树都比根节点小的特性。否则,就说明这不是一颗镜像搜索树,而是普通的二叉树。
然而如果你就通过上面的方法来判断这颗是什么树的话,其实是有问题的!其实这里还有一个地方容易被忽略,那就只用一次判断的方法来判断这是一颗什么树。这样带来的问题是,你不能够保证左子树也是颗搜索树,右子树也是颗搜索树!比如有这种情况:
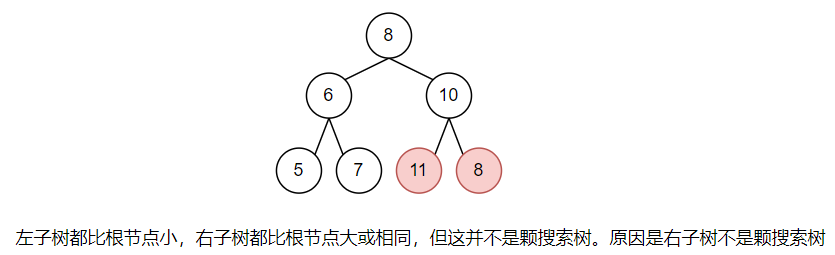
所以我们还要对左子树和右子树用同样的方法来判断是不是颗搜索树,从而才能保证这整一颗树是不是搜索树!我就是没有意识道这个点才浪费了好多的时间。:(
没错,左子树的左子树,左子树的右子树...也要用同样的方法判断。所以,用递归来解决啊!代码后面再给出吧。
知道了是搜索树还是镜像搜索树,接下来就好办了,我们可以通过先序序列,和对应的区间范围,按照搜索树的特性,通过递归得到后序遍历的序列。
如果是搜索树的话,大概思路就是,先把先序序列的第1个元素放到后序序列的最后一个位置,然后从第2个位置开始遍历先序序列,按照搜索树的特性找到右子树开始的位置,然后递归去求出左子树的后序序列和右子树的后序序列。镜像搜索树同理。
我用的方法是不需要建树的,AC代码如下:
1 #include <cstdio> 2 using namespace std; 3 4 bool isBST(int *pre, int left, int right, bool flag) { 5 if (left <= right) { // left为区间最左边的位置,right为区间最右边的位置,合法范围是left <= right 6 int i = left + 1, j; // i用于第一次遍历,记录右子树开始的位置。j用于第二次遍历,来判断这颗树是不是搜索树或是镜像搜索树 7 if (flag) { // flag == true,假定是搜索树,用搜索树的特性来遍历 8 for ( ; i <= right && pre[i] < pre[left]; i++); // i不断右移,直到某个元素比最左边的元素大或相等 9 for (j = i; j <= right && pre[j] >= pre[left]; j++);// j不断右移,直到某个元素小于最左边的元素小,退出循环。注意j要从i的位置开始! 10 } 11 else { // flag == false,假定是镜像搜索树,用镜像搜索树的特性来遍历 12 for ( ; i <= right && pre[i] >= pre[left]; i++); // i不断右移,直到某个元素比最左边的元素小 13 for (j = i; j <= right && pre[j] < pre[left]; j++); // j不断右移,直到某个元素不小于最左边的元素,退出循环 14 } 15 16 // 判断j是否在right的下一个位置,如果是则继续判断左右子树是不是搜索树或镜像搜索树,否则返回false。 17 return j == right + 1 ? isBST(pre, left + 1, i - 1, flag) && isBST(pre, i, right, flag) : false; 18 } 19 return true; 20 } 21 22 void getPost(int *pre, int *post, int preL, int postL, int n, bool flag) { 23 if (n == 0) return; 24 post[postL + n - 1] = pre[preL]; // 后序遍历的最后一个元素就是先序遍历的第一个元素 25 26 int i = 1; // 从下一个位置开始,找到右子树开始的位置 27 if (flag) for ( ; i < n && pre[preL + i] < pre[preL]; i++); 28 else for ( ; i < n && pre[preL + i] >= pre[preL]; i++); 29 30 getPost(pre, post, preL + 1, postL, i - 1, flag); // 递归得到左子树的后序遍历结果 31 getPost(pre, post, preL + i, postL + i - 1, n - i, flag); // 递归得到右子树的后序遍历的结果 32 } 33 34 int main() { 35 int n; 36 scanf("%d", &n); 37 int pre[n], post[n]; 38 for (int i = 0; i < n; i++) { 39 scanf("%d", pre + i); 40 } 41 42 bool flag = true; // true表示这颗树是搜索树,false表示这颗树是镜像搜索树,一开始假定为搜索树 43 if (n > 1 && pre[1] >= pre[0]) flag = false; // 如果第2个元素比第1个元素要大,flag改写为false,假定为镜像搜索树 44 45 // 判断这颗树是不是搜索树或是镜像搜索树 46 if (!isBST(pre, 0, n - 1, flag)) { // 如果都不是,就说明是普通的二叉树 47 printf("NO\n"); 48 } 49 else { // 如果是搜索树或镜像搜索树 50 printf("YES\n"); 51 getPost(pre, post, 0, 0, n, flag); // 获取后序遍历的结果 52 for (int i = 0; i < n; i++) { 53 if (i) printf(" "); 54 printf("%d", post[i]); 55 } 56 } 57 58 return 0; 59 }
无注释版:

#include <cstdio> using namespace std; bool isBST(int *pre, int left, int right, bool flag) { if (left <= right) { int i = left + 1, j; if (flag) { for ( ; i <= right && pre[i] < pre[left]; i++); for (j = i; j <= right && pre[j] >= pre[left]; j++); } else { for ( ; i <= right && pre[i] >= pre[left]; i++); for (j = i; j <= right && pre[j] < pre[left]; j++); } return j == right + 1 ? isBST(pre, left + 1, i - 1, flag) && isBST(pre, i, right, flag) : false; } return true; } void getPost(int *pre, int *post, int preL, int postL, int n, bool flag) { if (n == 0) return; post[postL + n - 1] = pre[preL]; int i = 1; if (flag) for ( ; i < n && pre[preL + i] < pre[preL]; i++); else for ( ; i < n && pre[preL + i] >= pre[preL]; i++); getPost(pre, post, preL + 1, postL, i - 1, flag); getPost(pre, post, preL + i, postL + i - 1, n - i, flag); } int main() { int n; scanf("%d", &n); int pre[n], post[n]; for (int i = 0; i < n; i++) { scanf("%d", pre + i); } bool flag = true; if (n > 1 && pre[1] >= pre[0]) flag = false; if (!isBST(pre, 0, n - 1, flag)) { printf("NO\n"); } else { printf("YES\n"); getPost(pre, post, 0, 0, n, flag); for (int i = 0; i < n; i++) { if (i) printf(" "); printf("%d", post[i]); } } return 0; }
还有一种更直接的解法,虽然比较暴力,还是说一下吧,或许你一开始的思路就是这样的。
这种方法是需要建一颗树的,思路就是:
代码的思路也是这样的,AC代码如下:
1 #include <cstdio> 2 #include <vector> 3 #include <algorithm> 4 using namespace std; 5 6 struct TNode { 7 int data; 8 TNode *left, *right; 9 }; 10 11 // 按照搜索树的规则,递归去插入节点,建树 12 TNode *buildTree(TNode *root, int value) { 13 if (root == NULL) { 14 root = new TNode; 15 root->data = value; 16 root->left = root->right = NULL; 17 } 18 else if (value < root->data) { 19 root->left = buildTree(root->left, value); 20 } 21 else { 22 root->right = buildTree(root->right, value); 23 } 24 return root; 25 } 26 27 void mirror(TNode *root) { 28 if (root) { 29 swap(root->left, root->right); // 对调左右子树 30 mirror(root->left); // 递归去对调左子树的左右子树 31 mirror(root->right); // 递归去对调右子树的左右子树 32 } 33 } 34 35 void preOrderTraversal(TNode *root, vector<int> &v) { 36 if (root) { 37 v.push_back(root->data); 38 preOrderTraversal(root->left, v); 39 preOrderTraversal(root->right, v); 40 } 41 } 42 43 void postOrderTraversal(TNode *root) { 44 static bool flag = false; 45 if (root) { 46 postOrderTraversal(root->left); 47 postOrderTraversal(root->right); 48 if (flag) printf(" "); 49 flag = true; 50 printf("%d", root->data); 51 } 52 } 53 54 int main() { 55 int n; 56 scanf("%d", &n); 57 int pre[n]; 58 TNode *root = NULL; 59 for (int i = 0; i < n; i++) { 60 scanf("%d", pre + i); 61 root = buildTree(root, pre[i]); // 输入元素的同时把元素往树里插 62 } 63 64 vector<int> v; // 用来记录这颗树先序遍历的结果 65 preOrderTraversal(root, v); 66 bool flag = true; // flag == true表示这颗树是搜索树 67 for (int i = 0; i < n; i++) { 68 if (v[i] != pre[i]) { // 某个元素不同 69 flag = false; // flag改写为false,不是搜索树了 70 break; 71 } 72 } 73 74 if (flag) { // 是搜索树,直接后序遍历就好了 75 printf("YES\n"); 76 postOrderTraversal(root); 77 } 78 else { // 不是搜索树,进一步判断是不是镜像搜索树 79 mirror(root); // 先对调这颗树的左右子树 80 v.clear(); // 之前有记录所以清空 81 preOrderTraversal(root, v); // 先序遍历对调后的这颗树,把结果记录在v中 82 flag = true; // 这是flag == true表示这颗树是镜像搜索树 83 for (int i = 0; i < n; i++) { 84 if (v[i] != pre[i]) { // 某个元素不同 85 flag = false; // flag改写为flase,连镜像搜索树也不是 86 break; 87 } 88 } 89 90 if (flag) { // flag == true,是镜像搜索树 91 printf("YES\n"); 92 postOrderTraversal(root); 93 } 94 else { // flag == false,不是镜像搜索树,也不是搜索树 95 printf("NO\n"); 96 } 97 } 98 99 return 0; 100 }
又写了篇字很多的题解。主要是不想写现在这个专业的论文啊!这个月要交三篇几千字的论文,而现在的我一个字都没动...虽然转专业去了计院,但是现在这个专业的论文还是要写啊,太难受了。还是写博客有趣。后面也没什么时间写算法题和博客了,赶紧过完这个月吧,假期我要继续享受AC(WA)带来的快感。
今天还是第一天高考,放平心态啊!不要像我一样...
浙大PAT 4-06. 搜索树判断 (解题思路):https://blog.csdn.net/a418382926/article/details/22597547
标签:open namespace stl nbsp ide loading 现在 spl 技术
原文地址:https://www.cnblogs.com/onlyblues/p/14859202.html