标签:有序 gif 通过 依次 个数 ima html 个性 log
简单地理解,满足以下两个条件的树就是二叉树:
本身是有序树;
树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
经过前人的总结,二叉树具有以下几个性质:
二叉树中,第 i 层最多有 2i-1 个结点。
如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2*n2。所以,n 用另外一种方式表示为 n=n1+2*n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
二叉树还可以继续分类,衍生出满二叉树和完全二叉树。
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
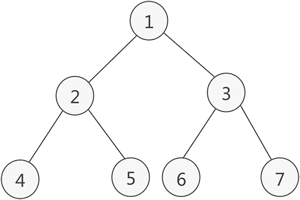
如图 2 所示就是一棵满二叉树。
满二叉树除了满足普通二叉树的性质,还具有以下性质:
满二叉树中第 i 层的节点数为 2n-1 个。
深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
具有 n 个节点的满二叉树的深度为 log2(n+1)。
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
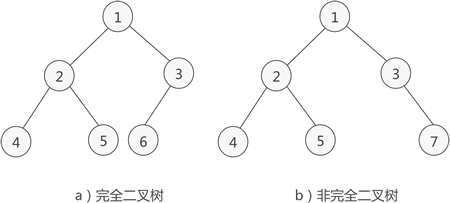
如图 3a) 所示是一棵完全二叉树,图 3b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ?log2n?+1。
?log2n? 表示取小于 log2n 的最大整数。例如,?log24? = 2,而 ?log25? 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如图 3a)),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
如果 2*i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2*i 。
如果 2*i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2*i+1 。
二叉树的存储结构有两种,分别为顺序存储和链式存储。
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
有读者会说,满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树的所有特征。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图 1 所示:
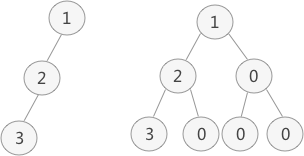
图 1 中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
解决了二叉树的转化问题,接下来学习如何顺序存储完全(满)二叉树。
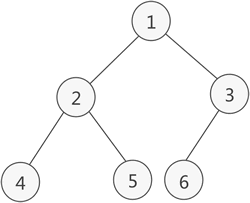
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
 --->
---> 
存储由普通二叉树转化来的完全二叉树也是如此
 --->
---> 
完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(0,1,2,3,...),
若节点 i 有左右孩子,则其左孩子节点为 2 * i + 1,右孩子节点为 2 * i+2。
此性质可用于还原数组中存储的完全二叉树
2、链式存储
 --->
---> 
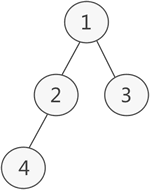
如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。
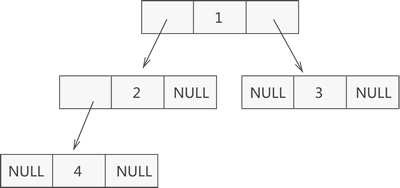
因此,图 1 对应的链式存储结构如图 2 所示:
由图 2 可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如图 3 所示):
指向左孩子节点的指针(Lchild);
节点存储的数据(data);
指向右孩子节点的指针(Rchild)

参考:http://data.biancheng.net/view/194.html
标签:有序 gif 通过 依次 个数 ima html 个性 log
原文地址:https://www.cnblogs.com/h--d/p/14894789.html