标签:pop blog turn queue 关于 多叉树 根据 mcc ref
树的路径长度,即树根到每个叶节点的距离之和。
树的带权路径长度,即树根到每个叶节点的距离与每个叶结点权值的乘积之和。
哈夫曼树,也叫 Huffman 树,就是 WPL 最短的一种最优多叉树。
对于哈夫曼树的构造,我们以二叉哈夫曼树为例:
我们每次选择两棵根节点权值最小的树,将它们的根节点合并成一棵新树。
原来的两个根节点成为为新树的根节点的儿子。新树的根节点权值为合并的两个根节点权值之和。
假设我们要构造一棵初始有五个节点的二叉哈夫曼树,权值分别为 \(1,2,4,6,8\),则它们的构建过程如下:
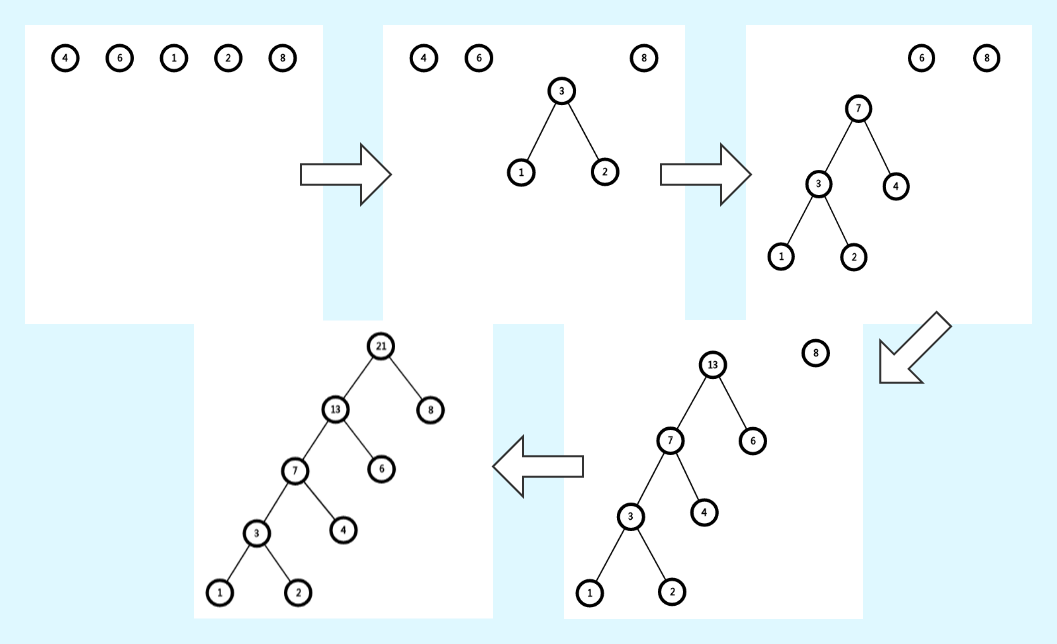
(我腾讯文档没有 VIP 所以下载不了高清图片,只能将就看吧 qwq)
注意,哈夫曼树中允许多个点有相同的权值。
假设我们要构造一棵 \(k\) 叉哈夫曼树 \((k>2)\)。
根据以上对哈夫曼树构造的原理,可以发现,这个构造方法是基于贪心的思想。每次取出最小的 \(k\) 个节点来合并成新的节点。
但是如果最后一步合并时,可选节点的数量不足 \(k\) 个,就会出现合并后的哈夫曼树根节点的儿子数小于 \(k\) 的情况。
此时它就不是一颗 WPL 最小的最优 \(k\) 叉树。因为此时我们随便取一个叶节点当做根节点的儿子,都可使 \(\sum (w_i\times l_i)\) 的值变小。
所以我们要满足 \((k-1)\mid (n-1)\) 这个条件时,才能使构造的 \(k\) 叉哈夫曼树达到最优。
而要满足这个条件,我们可以不断向图中加入权值为 \(0\) 的节点。显然 \(0\) 节点一定会先合并,这样可以使有权节点的深度降低。
哈夫曼编码的原则是:编码从叶子节点到根节点,译码从根节点到叶子节点。
但其实这句话对下面的内容并没有什么帮助。
我们还是以二叉哈夫曼树为例。
对于一棵二叉哈夫曼树,我们从根节点开始,对左子树编码 \(0\),对右子树编码 \(1\),直到遍历完整棵树。
此时我们再从根节点出发,将路径上的编码排列起来,一直到某个根节点,此时的编码串就是该根节点的哈夫曼编码。
举个例子,我们有一串电文 AMCADEDDMCCAD,需要将其翻译成 01 串,并使其尽量短。
我们统计每个字符的出现次数,可得到如下数据:
\(\begin{array}{ccc} E & M & C & A & D \\hline 1 & 2 & 3 & 3 & 4\\end{array}\)
我们将每种字符的出现次数作为节点的权值,可建造一棵如图所示的二叉哈夫曼树:
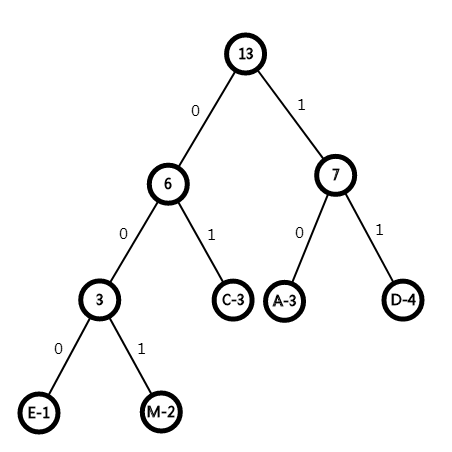
所以可得到各个字符的哈夫曼编码:
\(\begin{array}{c|cc} E&001\M&000\C&01\A&10\D&11\\end{array}\)
根据哈夫曼编码的定义,我们也可以看出,每种字符的编码长度之和为 PL,而每种字符的编码长度与其出现次数的乘积之和为 WPL。
此时的 PL 不一定是最短的,但 WPL 一定是最短的,只有这样才能使原串翻译后的 01 串最短。
当然上面只是说二叉哈夫曼树,其编码也只包含两种字符。假若要用 \(k\) 进制数来表示一个字符串,我们可以将其建成 \(k\) 叉哈夫曼树 \((k\ge 2)\)。
对于代码的具体实现,结合下面的例题来说。
有一个由 \(n\) 种字符组成的字串,给出这 \(n\) 种字符的出现次数,用 \(k\) 进制数来表示这个字符串。
求出这个 \(k\) 进制数的最短长度,并求出此时编码最长的字符的最短编码长度。
NOI 出模板题(
直接根据每种字符的出现次数建 \(k\) 叉哈夫曼树。
第一问就是 WPL 的长度,第二问就是在树中深度最大的字符的深度减一。
至于实现,我们运用优先队列存储每个节点的权值和深度,并按权值为第一关键字,深度为第二关键字从大到小排序。
首先将每个节点自己作为一棵树,放到优先队列中,并不断加入 \(0\) 节点直到满足条件为止。
每次取出 \(k\) 个节点来合并,同时统计 WPL。最后优先队列中只剩一个节点,输出统计结果与其深度减一即可。
struct node{
int w,h;
bool operator < (const node &a) const{
return a.w==w?h>a.h:w>a.w;
}
};
signed main(){
n=read();k=read();priority_queue<node> q;
for(int i=1,w;i<=n;i++) w=read(),q.push((node){w,1});
while((q.size()-1)%(k-1)) q.push((node){0,1});
while(q.size()>=k){
int h=-1,w=0;
for(int i=1;i<=k;i++){
node t=q.top();q.pop();
h=max(h,t.h);w+=t.w;
}
ans+=w;
q.push((node){w,h+1});
}
printf("%lld\n%lld\n",ans,q.top().h-1);
return 0;
}
没啦,啥都没啦。
标签:pop blog turn queue 关于 多叉树 根据 mcc ref
原文地址:https://www.cnblogs.com/KnightL/p/14902399.html