标签:改变 机器 pen 装箱 模板题 含义 sizeof scanf 避免
斜率优化的中心思想就是利用一次函数的斜率来优化某些 \(DP\) 转移方程。斜率优化的题目状态转移方程通常比单调队列优化更为复杂,同时斜率优化通常也会用到单调队列优化。
以下记录的题目基本上都为斜率优化的模板题。
本题的题意较为复杂。一台机器需要按顺序处理 \(n\) 个任务,每个任务都有一个花费时间 \(t_i\) 和花费系数 \(c_i\)。将 \(n\) 个任务分成若干组处理,每组任务处理前都要花费 \(s\) 的启动时间。 每组任务的花费为从第一组任务开始前到本组任务结束后的总时间乘以该组任务的花费系数之和。求最小的花费总和。
本题可以分为三个步骤来思考。
首先考虑朴素的状态转移。
为了表示方便,以下的 \(t_i\) 和 \(c_i\) 均表示 \(t_i\) 和 \(c_i\) 的前缀和。
定义 \(f[i]\) 表示完成前 \(i\) 个任务的最小花费。通过理解题意可以发现,如果将 \(j+1\) ~ \(i\) 分为一组,那么在第 \(j+1\) 个任务之前的启动时间 \(s\) 会对之后的所有任务的花费造成影响,即花费增加了 \((c_n-c_j)*s\) 。得到这个性质后,就可以写出朴素的状态转移方程:
\(f[i]=min(f[j]+(c[i]-c[j])*t[i]+(c[n]-c[j])*s)\) 。其中 \(0 \leq j \leq i-1\) 。
显然,时间复杂度为 \(O(n^2)\) ,无法通过本题。但可以通过简化版,其中 \(n \leq5000\) 。
for(int i=1;i<=n;i++)
for(int j=0;j<i;j++)
f[i]=min(f[i],f[j]+(c[i]-c[j])*t[i]+(c[n]-c[j])*s);
斜率优化的推导。
先省略 \(min\) ,通过拆项、移项可以得到以下方程 :
\(f[j]=(t[i]+s)*c[j]+f[i]-c[i]*t[i]-c[n]*s\) 。
如果将 \(f[j]\) 看成 \(y\) ,将 \(c[j]\) 看成 \(x\) ,那么 \((c[j],f[j])\) 就是平面直角坐标系上的一点。同时当 \(i\) 固定时,方程只有这两个变量,那么就可以将化简得到方程表示为 \(y=k*x+b\) ,也就是一个一次函数的表达式。其中\(k=t[i]+s,b=f[i]-c[i]*t[i]-c[n]*s\)。
而现在需要求的是 \(f[i]\) 的最小值,也就是 \(b\) 的最小值。同时对于每一个 \(i,k\) 都是确定的。那么也就可以将 \(y=k*x-inf\) 这条直线向上平移,遇到的第一个 \((c[j],f[j])\) 就是最优解。如下图所示。

那么哪些点可以成为最优解呢,通过观察可以发现,只有最外侧的点可以成为最优解,在数学上称为凸包,此时就可以将其余的点删去。如下图所示
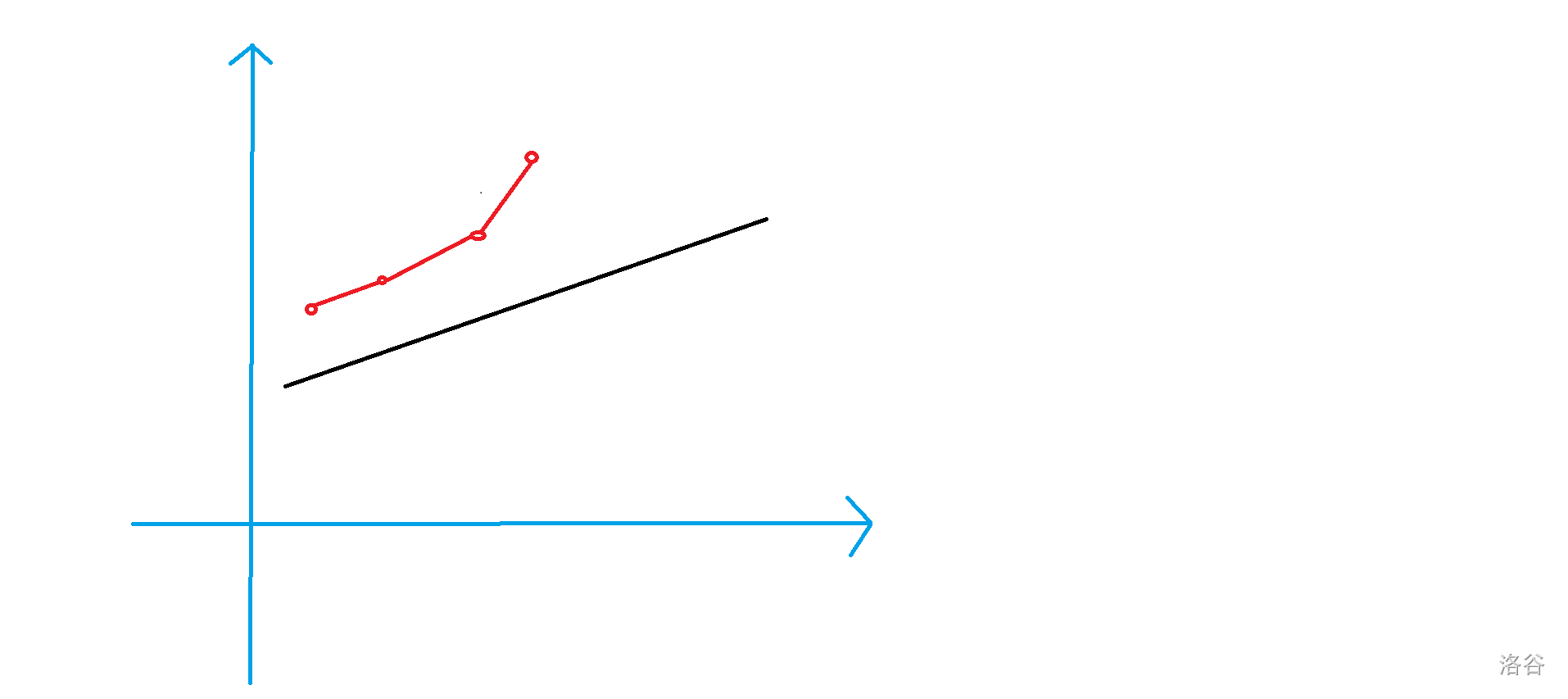
可以发现,对于凸包上两点间的直线的斜率是单调递增的。
接下来的问题就是怎么求出每一个 \(k\) 所对应的点坐标,由于最坏情况下凸包的点的数量会达到 \(n\) ,可能会被良心出题人卡,所以无法直接使用枚举。
通过观察又可以发现,对于每一个 \(k\) ,向上平移的直线第一个遇到的点的\(k_j\)一定是大于\(k\) 的最小值 ,同时 \(k=t[i]+s\) 显然是单调递增的。那么对于一个点,它和凸包上后一个点的斜率 \(k_j\) 如果小于当前的 \(t[i]+s\),那么肯定也小于之后的 \(t[i‘]+s\),于是就可以用到单调队列优化。
在查询之前,将所有斜率小于 \(k\) 的点直接删去即可。同时对于每一个新加入的点 \((c[i],f[i])\) ,这个点的坐标显然是在所有点的右侧,那么这个点显然是当前凸包内的一点,那么在插入的时候删去所有不在凸包上的点即可。删除的情况如下图所示
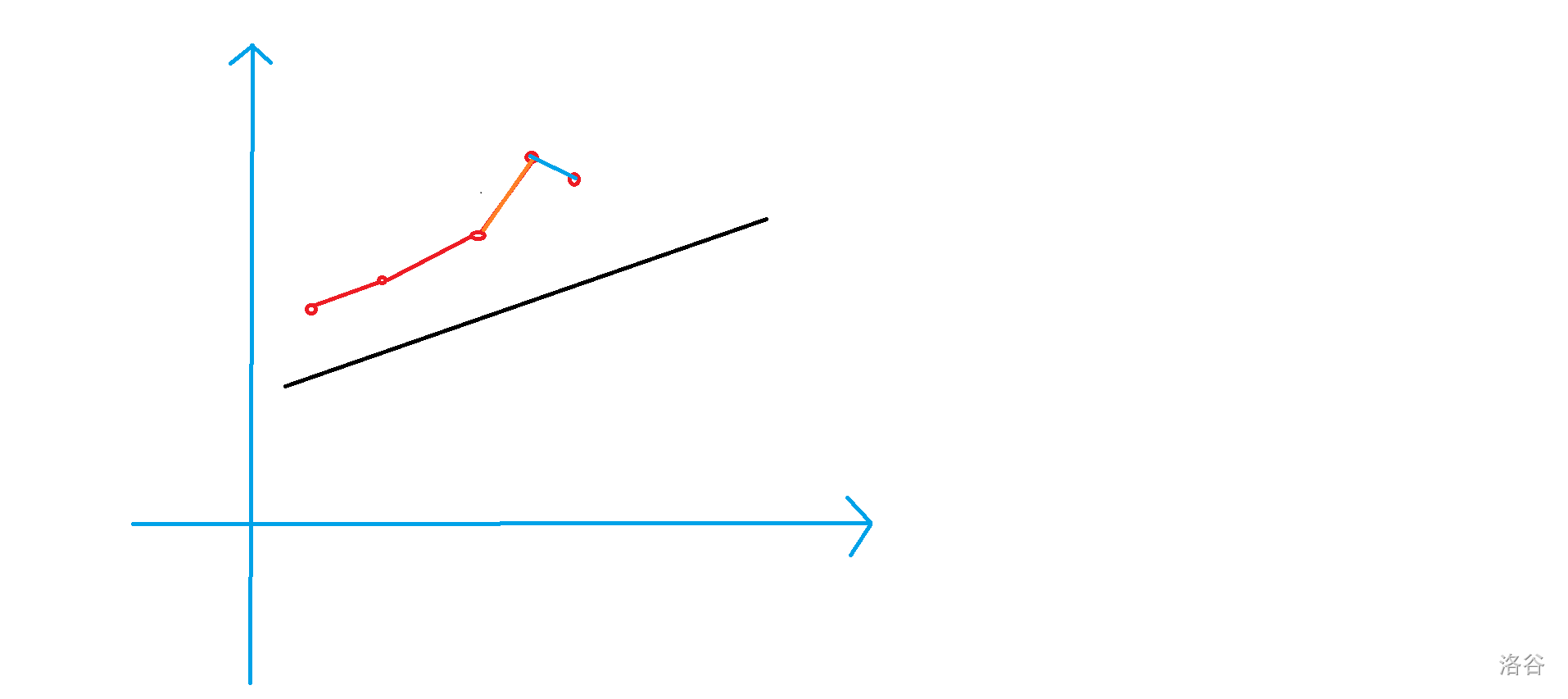
橙色边所指向的点原来是在凸包上,当新添加蓝色边所指向的点时就不在凸包上了,直接删去这个点就可以了。用不等式来表示。即
当 \(\dfrac{f_{h+1}-f_h}{c_{h+1}-c_h} \leq t_i+s\) 时队首出队;
当 \(\dfrac{f_{tt}-f_{tt-1}}{c_{tt}-c_{tt-1}} \geq \dfrac{f_{i}-f_{tt}}{c_{i}-c_{tt}}\) 时队尾出队。
在实际运用时,为了避免精度误差,通常会交叉相乘避免除法运算。
for(int i=1;i<=n;i++)
{
while(hh<tt&&f[q[hh+1]]-f[q[hh]]<=(t[i]+s)*(c[q[hh+1]]-c[q[hh]])) hh++;
f[i]=f[q[hh]]+(c[i]-c[q[hh]])*t[i]+(c[n]-c[q[hh]])*s;
while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) tt--;
q[++tt]=i;
}
但是代码提交上去也只能得到 \(60\) 分。再次观察题目,会发现一个很有趣的地方,\(|t_i| \leq 2^8\),也就是说, \(t_i\) 可能为负数(这里的 \(t_i\) 指题意中的 \(t_i\)),那么就不满足 \(t_i\) (这里的 \(t_i\) 指前缀和) 单调递增了,那么也就不满足 \(k\) 单调递增了。于是还需进一步优化。
最终的解法。
虽然说每一个任务的完成时间为负数,但是对于队尾的出队判断和状态转移方程是无影响的,所以只需要改变队头出队。其实这里就不需要出队了,也就是可以将队列改成栈。而查找的工作就交给了二分法。于是就可以愉快的通过本题了。
#include<cstdio>
#include<cstring>
const int N=3e5+10;
#define int long long
int f[N],n,s,t[N],c[N],q[N];
int min(int a,int b){return a<b?a:b;}
signed main()
{
scanf("%lld%lld",&n,&s);
for(int i=1;i<=n;i++)
{
scanf("%lld%lld",&t[i],&c[i]);
t[i]+=t[i-1];
c[i]+=c[i-1];
}
memset(f,0x3f,sizeof(f));
f[0]=0;
int hh=1,tt=1;
q[1]=0;
for(int i=1;i<=n;i++)
{
int l=hh,r=tt;
while(l<r)
{
int mid=(l+r)>>1;
if((f[q[mid+1]]-f[q[mid]])> (t[i]+s)*(c[q[mid+1]]-c[q[mid]])) r=mid;
else l=mid+1;
}
f[i]=f[q[r]]+(c[i]-c[q[r]])*t[i]+(c[n]-c[q[r]])*s;
while(hh<tt&&(double)(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(double)(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) tt--;
q[++tt]=i;
}
printf("%lld\n",f[n]);
return 0;
}
本题需要一定的转化变形技巧。
给定 \(n\) 座山(每座山的大小都可以忽略不计),第 \(i\) 座山和第 \(i-1\) 座山之间的距离为 \(D_i\),有\(m\) 只猫,\(p\) 位饲养员。第\(i\) 只猫要在第 \(h_i\) 座山上玩 \(T_i\) 时间。每个饲养员从 \(1\) 号山出发,出发的时间任意(可以从负数出发),每单位时间走单位路程,路上遇到已经玩好的猫会将它带走。求所有猫等待时间之和的最小值。
首先可以发现,每一个饲养员都从 \(1\) 号出发,那么就可以用前缀和先求出每一座山到起点的距离,也就是将 \(D_i\) 的含义转化为第 \(i\) 座山到第 \(1\) 座山的距离。对于每一位饲养员的出发时间 \(s_i\) ,他能接到第 \(j\) 只猫的充要条件为 \(s_i+d_{h_j}\geq t_j\) ,移项可以得到 \(s_i\geq t_j-d_{h_j}\)。
而对于每一只猫,等待的时间就为 \(s_i-(t_j-d_{h_j})\)。可以发现,对于题目有用的是 \((t_j-d_{h_j})\),于是就可以定义 \(a_j=t_j-d_{h_j}\)。其实也就是表示第 \(j\) 只猫恰好刚玩好就被接走时,饲养员出发的时间点。
由于题目中并未要求按顺序接走每一只猫。于是就可以将 \(a\) 数组从小到大排序,那么题目就转化为将这 \(n\) 只猫分成至多连续的 \(p\) 组。设第 \(i\) 组的第一只猫排序后的编号为 \(l\),最后一只猫排序后的编号为 \(r\)。显然恰好接走最后一只猫等待的时间最少,即出发时间点为 \(a_r\),那么那么这一组猫等待的总时间就为 \((a_r-a_l+a_r-a_{l+1}+...+a_r-a_r)\),
稍微变化一下,就可以得到
\((a_r*(r-l+1)-(a_l+a_{l+1}+...+a_r))\)。
于是就可以定义 \(sum\) 数组来记录 \(a\) 的前缀和。
定义 \(f[j][i]\) 表示 \(j\) 个饲养员一共接走了 \(i\) 只猫时所等待的最小总时间。那么就可以得出状态转移方程:
\(f[j][i]=min(f[j-1][k]+a_i*(i-k)-(sum_i-sum_k))\),其中 \(0 \leq k \leq i-1\) 。
考虑斜率优化。
去括号、移项,得:\(f[j-1][k]+sum_k=a_i*k+f[j][i]-a_i*i+sum_i\)。
于是 \(y=f[j-1][k]+sum_k,x=k,k=a_i,b=f[j][i]-a_i*i+sum_i\)。
接下来的步骤就和上一题中的 \(Part\) \(2\) 相似了。最终的时间复杂度就为 \(O(pm)\) 。
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+10;
const int M=1e5+10;
const int P=110;
#define int long long
int n,m,p,d[N],a[N],sum[N],f[P][M],q[N];
signed main()
{
scanf("%lld%lld%lld",&n,&m,&p);
for(int i=2;i<=n;i++)
{
scanf("%d",&d[i]);
d[i]+=d[i-1];
}
for(int h,t,i=1;i<=m;i++)
{
scanf("%lld%lld",&h,&t);
a[i]=t-d[h];
}
sort(a+1,a+m+1);
for(int i=1;i<=m;i++) sum[i]=a[i]+sum[i-1];
memset(f,0x3f,sizeof(f));
for(int i=0;i<=p;i++) f[i][0]=0;
for(int j=1;j<=p;j++)
{
int hh=1,tt=1;
q[1]=0;
for(int i=1;i<=m;i++)
{
while(hh<tt&&f[j-1][q[hh+1]]+sum[q[hh+1]]-f[j-1][q[hh]]-sum[q[hh]]<=a[i]*(q[hh+1]-q[hh])) hh++;
int k=q[hh];
f[j][i]=f[j-1][k]+a[i]*(i-k)-(sum[i]-sum[k]);
while(hh<tt&&(f[j-1][q[tt]]+sum[q[tt]]-f[j-1][q[tt-1]]-sum[q[tt-1]])*(i-q[tt])>=(f[j-1][i]+sum[i]-f[j-1][q[tt]]-sum[q[tt]])*(q[tt]-q[tt-1])) tt--;
q[++tt]=i;
}
}
printf("%lld\n",f[p][m]);
return 0;
}
给定 \(n\) 块土地,每块土地有一个长度 \(w\) 和宽度 \(l\) 将若干个土地一起购买的花费为\(maxw*maxl\)。求购买所有的土地的花费的最小值。
首先可以注意到,题意中并未要求按顺序购买,那么就可以先对于长和宽其中之一从小到大进行排序,这里对 \(l\) 先进行排序。如果对于 \(j \leq i-1\) ,且满足 \(w[j] <w[i],l[j]<l[i]\),那么 \(i\) 和 \(j\) 一起购买显然更优,那么也就没有必要考虑 \(j\) 了,所以真正有用的 \(j\) 需要满足 \(l[j]>l[i]\) ,那么就可以先将排序,求出有用的 \(i\) 排成的序列,可以发现对于这个序列,\(l\) 单调递增, \(w\) 单调递减。那么对于连续的 \(h\) ~\(t\) 这些土地,将这些土地一起购买的花费显然为 \(w[k]*l[t]\) 。可以发现,这样的购买方法一定比其他购买方法更优。于是接下来又是将这个序列分成若干组,求最小值了。
定义 \(f[i]\) 表示购买排序后前 \(i\) 个有用的土地所花费的最小值。那么就有:
\(f[i]=min(f[j]+w[j+1]*l[i])\) ,其中 \((0\leq j \leq i-1)\)。
时间复杂度为 \(O(n^2)\),于是要用到斜率优化。
移项,最终得:\(f[j]=-l[i]*w[j+1]+f[i]\)。
\(y=f[j],x=w[j+1],k=-l[i],b=f[i]\)。
那么最终需要维护的凸包就要满足 $\dfrac{f[i]-f[j]}{w[i+1]-w[j+1]} $
单调递增。但是需要注意的是,这里的斜率是负数,因为 \(k=-l[i]\),同时 \(w[i]\) 是单调递减的。所以说在交叉相乘的时候需要改变符号方向。
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=5e4+10;
#define int long long
int n,f[N],q[N];
struct node{
int w,l;
bool operator <(const node &t)const{
if(t.w==w) return l>t.l;
return w>t.w;
}
}a[N],b[N];
signed main()
{
//freopen("233.in","r",stdin);
scanf("%lld",&n);
for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].w,&a[i].l);
sort(a+1,a+n+1);
int tot=0;
for(int i=1;i<=n;i++)
{
if(a[i].l>b[tot].l) b[++tot]=a[i];
}
n=tot;
int hh=1,tt=1;
q[1]=0;
for(int i=1;i<=n;i++)
{
while(hh<tt&&(f[q[hh]]-f[q[hh+1]])>=b[i].l*(b[q[hh+1]+1].w-b[q[hh]+1].w)) hh++;
f[i]=f[q[hh]]+b[i].l*b[q[hh]+1].w;
while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(b[i+1].w-b[q[tt]+1].w)<=(f[i]-f[q[tt]])*(b[q[tt]+1].w-b[q[tt-1]+1].w)) tt--;
q[++tt]=i;
}
printf("%lld\n",f[n]);
return 0;
}
推导公式的时候一定要仔细。
给定 \(n\) 个长度为 \(c_i\),宽度为 \(1\) 的玩具,将他们按顺序放到若干个箱子里,每一个箱子中的两个玩具之间需要单位长度的空隙。那么每一个箱子就有一个长度 \(x\),每一个箱子的花费就为 \((x-L)^2\) ,其中 \(L\) 是一个常数,在输入时给出。求最小的总花费。
首先可以发现,只需要知道每一段连续的玩具长度,那么就可以先用前缀和处理 \(c_i\),那么对于一个左端点为 \(i\) ,右端点为 \(r\) 的箱子,长度 \(x=i-j+s[i]-s[j-1]\) 。同时为了方便计算,可以将 \(c_i\) 变成 \(c_i+1\),那么 \(x=s[i]-s[j-1]-1-l\),又可以将 \(L\) 提前 \(+1\) ,于是就可以定义 \(f[i]\) 表示前 \(i\) 个箱子的最小花费。可以得出状态转移方程,即:
\(f[i]=min(f[j]+(x-l)*(x-l))\),其中 \(x=s[i]-s[j],0 \leq j \leq i-1\)。
接着考虑斜率优化。
拆项,移项,最终得:
\(f[j]+l^2+s[j]^2+2*i*s[j]=2*s[i]*s[j]+f[i]+s[i]^2-2*s[i]*l\)。
于是 \(y=f[j]+l^2+s[j]^2+2*i*s[j],x=s[j],k=2*s[i]\)。
同时注意到 \(k\) 是单调递增的,于是就可以用单调队列优化凸包。
#include<cstdio>
using namespace std;
const int N=5e4+10;
#define int long long
int n,l,s[N],f[N],q[N];
int min(int a,int b){return a<b?a:b;}
int get_y(int j){ return f[j]+2*s[j]*l+s[j]*s[j]+l*l;}
int get_x(int j){ return s[j];}
signed main()
{
//freopen("233.in","r",stdin);
scanf("%lld%lld",&n,&l);
for(int i=1;i<=n;i++) scanf("%lld",&s[i]),s[i]+=s[i-1]+1;
int hh=1,tt=1;
l++;
q[1]=0;
for(int i=1;i<=n;i++)
{
while(hh<tt&&get_y(q[hh+1])-get_y(q[hh])<=2*s[i]*(get_x(q[hh+1])-get_x(q[hh]))) hh++;
int j=q[hh],x=s[i]-s[j]-l;
f[i]=f[j]+x*x;
while(hh<tt&&(get_y(q[tt])-get_y(q[tt-1]))*((get_x(i))-get_x(q[tt]))>=(get_y(i)-get_y(q[tt]))*((get_x(q[tt]))-get_x(q[tt-1]))) tt--;
q[++tt]=i;
}
printf("%lld\n",f[n]);
return 0;
}
对于斜率优化 \(DP\) ,首先需要确定朴素的状态转移方程。然后进行移项,对于一次函数 \(y=kx+b\) ,通常情况下将在 \(j\) 确定时的常量(也就是只和 \(j\) 有关或本身就是常量)放在等式的左边作为 \(y\) ,将同时与 \(i,j\) 有关的项放在等式右边(通常是几个单项式相乘),其中与 \(j\) 有关的单项式作为 \(x\) ,与 \(i\) 有关的项作为 \(k\) ,其余的只和 \(i\) 有关的项作为 \(b\) 。
如果 \(k\) 的值单调递增,那么就可以用单调队列优化,小于当前 \(k\) 的凸包上的点直接删去,如果 \(k\) 的值无单调性,就可以用二分法找到第一个和下一个点之间连线的斜率大于 \(k\) 的点。最后在新添 \(i\) 点的时候维护一下凸包即可。此时通常可以用交叉相乘避免精度误差。
最后得到的即为答案。
标签:改变 机器 pen 装箱 模板题 含义 sizeof scanf 避免
原文地址:https://www.cnblogs.com/NLCAKIOI/p/14916918.html