标签:image 出错 变化 ade 定义 乘法 code 没有 函数
设函数\(y = f(x)\)在点\(x_0\)的某个邻域内有定义,当自变量\(x\)在\(x_0\)处有增量\(Δx\),\((x_0+Δx)\)也在该邻域内时,相应地函数取得增量\(Δy = f(x_0+Δx)-f(x_0)\)如果\(Δy\)与\(Δx\)之比当\(Δx→0\)时极限存在,则称函数\(y=f(x)\)在点\(x_0\)处可导,并称这个极限为函数\(y=f(x)\)在点\(x_0\)处的导数
好高级的样子。。。
怎么用人话表述呢
说白了就是给定函数\(f(x)\),则其平均变化率为\(\frac {f(x + \Delta x) - f(x)} {\Delta x}\)当\(\Delta x\)趋近于负无穷,平均变化率的极限为\(\lim _ {\Delta x\rightarrow 0} \frac {f(x + \Delta x) - f(x)} {\Delta x}\)此时我们称该式为\(f(x)\)的导数,记作\(f‘(x)\)
所以说
同时,在数学中以下两者是等价的
如果函数\(y=f(x)\)在开区间内每一点都可导,就称函数\(f(x)\)在区间内可导。这时函数\(y=f(x)\)对于区间内的每一个确定的x值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数\(y=f(x)\)的导函数,记作\(y‘\)、\(f‘(x)\)、\(dy/dx\) 或 \(df(x)/dx\) ,简称导数。
换成几何意义的话可能会更好理解:导数的几何意义是该函数曲线在这一点的切线斜率
那么知道了定义,以下是一些常见函数的导函数
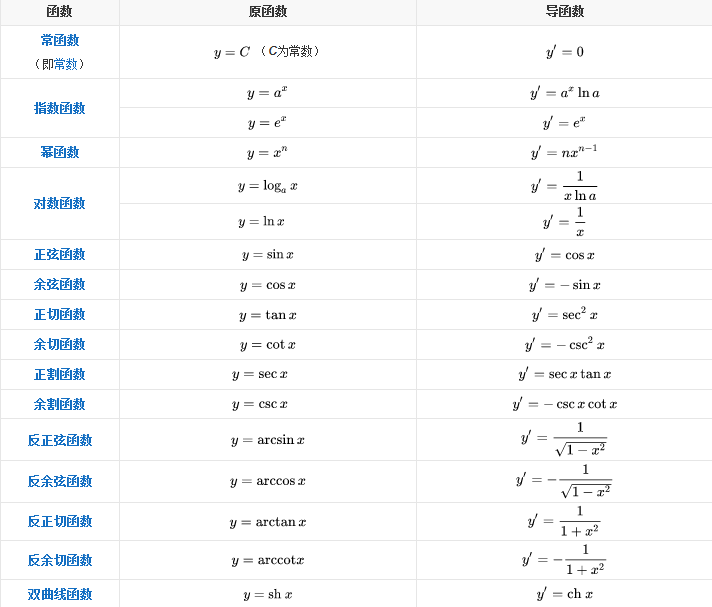
加法法则
减法法则
乘法法则
除法法则
本人比较菜,所以这一篇博客只写了导数最基础的知识,没有复杂的公式,更没有例题,因为我现在在学校并没有学习导数,目前只是出于兴趣提前看看,所以不是很精,有的地方可能会出错,大佬勿喷,如果有错误请一定要告诉我呜呜呜呜多谢了QAQ,同时由于是自己随便学的,所以相关定理和例题并没有章法,就是学到啥了有感触了就写一点,这篇博客随着我学的越来越多会逐渐更新上题和深度学的东西的,不定期更新!
标签:image 出错 变化 ade 定义 乘法 code 没有 函数
原文地址:https://www.cnblogs.com/Crazyman-W/p/14928508.html