[SCOI2003]严格N元树

标签：stat   oid   operator   strlen   nbd   sizeof   alt   tor   节点   

Description
如果一棵树的所有非叶节点都恰好有 \(n\) 个儿子，那么我们称它为严格 \(n\) 元树。如果该树中最底层的节点深度为 \(d\)（根的深度为 \(0\)），那么我们称它为一棵深度为 \(d\) 的严格 \(n\) 元树。例如，深度为２的严格２元树有三个，如下图：

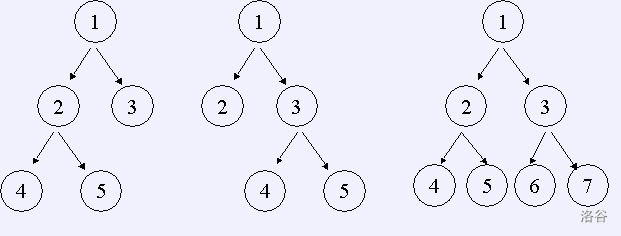
给出 \(n,d\)，编程数出深度为 \(d\) 的 \(n\) 元树数目。

Input
仅包含两个整数 \(n,d(0<n \leqslant 32,0 \leqslant d \leqslant 16)\)。输入数据保证你不需要考虑某一层多于 10241024 个节点的树（即 \(nd \leqslant 1024\)）。提示：答案保证不超过 200 位十进制数。

Output
仅包含一个数，即深度为 \(d\) 的 \(n\) 元树的数目。

Sample Input 1

2 2

Sample Output 1

3

Sample Input 2

2 3

Sample Output 2

21

Sample Input 3

3 5

Sample Output 3

58871587162270592645034001

我们首先考虑\(n=2\)的情况，记\(F_x\)表示深度为\(x\)的严格\(n\)元树个数，\(S_x=\sum\limits_{i=1}^xF_i\)，我们考虑\(F_x\)如何转移到\(F_{x+1}\)

考虑到深度增加，故我们新引入一个根节点，不难发现，\(F_{x+1}\)的所有情况，其左右子树的深度均小于\(x+1\)，故可得所有的情况数为\(S_x^2\)。显然，在这些情况中存在不合法的情况，因为要保证深度为\(x+1\)，故子树至少有一个深度需要达到\(x\)，用容斥原理可得\(F_{x+1}=S_x^2-S_{x-1}^2\)

那\(n\neq 2\)呢？很显然这\(n\)个子节点是互相独立的，故可得\(F_{x+1}=S_x^n-S_{x-1}^n\)

/*program from Wolfycz*/
#include<map>
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define Fi first
#define Se second
#define ll_inf 1e18
#define MK make_pair
#define sqr(x) ((x)*(x))
#define pii pair<int,int>
#define int_inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline char gc(){
	static char buf[1000000],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}
template<typename T>inline T frd(T x){
	int f=1; char ch=gc();
	for (;ch<‘0‘||ch>‘9‘;ch=gc())	if (ch==‘-‘)    f=-1;
	for (;ch>=‘0‘&&ch<=‘9‘;ch=gc())	x=(x<<1)+(x<<3)+ch-‘0‘;
	return x*f;
}
template<typename T>inline T read(T x){
	int f=1; char ch=getchar();
	for (;ch<‘0‘||ch>‘9‘;ch=getchar())	if (ch==‘-‘)	f=-1;
	for (;ch>=‘0‘&&ch<=‘9‘;ch=getchar())	x=(x<<1)+(x<<3)+ch-‘0‘;
	return x*f;
}
inline void print(int x){
	if (x<0)	putchar(‘-‘),x=-x;
	if (x>9)	print(x/10);
	putchar(x%10+‘0‘);
}
const int maxn=1e2;
const int base=1e4;
const int digit=4;
struct Bignum{
	int V[maxn],len;
	Bignum(){memset(V,0,sizeof(V)),len=1;}
	void init(){V[0]=1;}
	void read(char *s){
		int l=strlen(s),t=1;
		reverse(s,s+l); len=(l-1)/digit+1;
		for (int i=0;i<l;i++)	V[i/digit]+=(s[i]-‘0‘)*t,t*=10,t%=base;
	}
	void write(){
		printf("%d",V[len-1]);
		for (int i=len-2;~i;i--)	printf("%0*d",digit,V[i]);
		putchar(‘\n‘);
	}
}F[maxn],S[maxn];
Bignum operator +(Bignum x,Bignum y){
	Bignum z; z.len=max(x.len,y.len);
	for (int i=0;i<z.len;i++)	z.V[i]+=(x.V[i]+y.V[i]),z.V[i+1]+=z.V[i]/base,z.V[i]%=base;
	while (z.V[z.len])	z.V[z.len+1]+=z.V[z.len]/base,z.V[z.len]%=base,z.len++;
	return z;
}
Bignum operator -(Bignum x,Bignum y){
	Bignum z; z.len=max(x.len,y.len);
	for (int i=0;i<z.len;i++){
		z.V[i]+=(x.V[i]-y.V[i]);
		if (z.V[i]<0)	z.V[i]+=base,z.V[i+1]--;
	}
	while (!z.V[z.len]&&z.len>1)	z.len--;
	while (z.V[z.len])	z.V[z.len+1]+=z.V[z.len]/base,z.V[z.len]%=base,z.len++;
	return z;
}
Bignum operator *(Bignum x,Bignum y){
	Bignum z; z.len=x.len+y.len;
	for (int i=0;i<x.len;i++)
		for (int j=0;j<y.len;j++)
			z.V[i+j]+=x.V[i]*y.V[j],z.V[i+j+1]+=z.V[i+j]/base,z.V[i+j]%=base;
	while (!z.V[z.len]&&z.len>1)	z.len--;
	while (z.V[z.len])	z.V[z.len+1]+=z.V[z.len]/base,z.V[z.len]%=base,z.len++;
	return z;
}
Bignum mlt(Bignum a,int b){
	Bignum res; res.init();
	for (;b;b>>=1,a=a*a)	if (b&1)	res=res*a;
	return res;
}
int main(){
//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	int n=read(0),d=read(0);
	F[0].V[0]=1,F[1].V[0]=1;
	S[0]=F[0],S[1]=F[0]+F[1];
	for (int i=2;i<=d;i++){
		F[i]=mlt(S[i-1],n)-mlt(S[i-2],n);
		S[i]=S[i-1]+F[i];
	}
	F[d].write();
	return 0;
}

[SCOI2003]严格N元树

标签：stat   oid   operator   strlen   nbd   sizeof   alt   tor   节点   

原文地址：https://www.cnblogs.com/Wolfycz/p/14939155.html