标签:原理 art def long put lazy void 长大 区间
优雅,永不过时。
艺术的暴力,暴力的艺术——分块。
没错,不是文艺平衡树,而是文艺分块术!!!
您需要写一种数据结构,来维护一个长度为 \(n\) 的有序数列 \(A\),其中 \(A_i=i\) 。
其中需要提供以下操作:反转一个区间,例如原有序列是 5 4 3 2 1 ,反转区间是 [2,4] 的话,结果是 5 2 3 4 1 。
一共有 \(m\) 次操作,每次给定两个整数 \(l,r(l<r)\) 表示反转 \([l,r]\) 的元素。
输出 \(m\) 次操作后的序列。
正解显然是文艺平衡树,然而块状链表也可以维护这样的一个序列,来看看此题的块状链表解法。
根据分块思想的“大段维护,局部暴力”的思想,可以分开考虑 \([l,r]\) 在同一块内和不在同一块内的情况。
若 \([l,r]\) 在同一块内,直接暴力 swap ,复杂度 \(O(\sqrt n)\) 。
若 \([l,r]\) 不在同一块内,那么需要考虑整段如何维护(设计标记),局部如何暴力。
在此之前,不妨先来看看链表、块状链表是如何支持区间翻转的:
假设现在有一个包含 1 2 3 4 5 的链表,现在要翻转区间 [2,4] ,如下图:
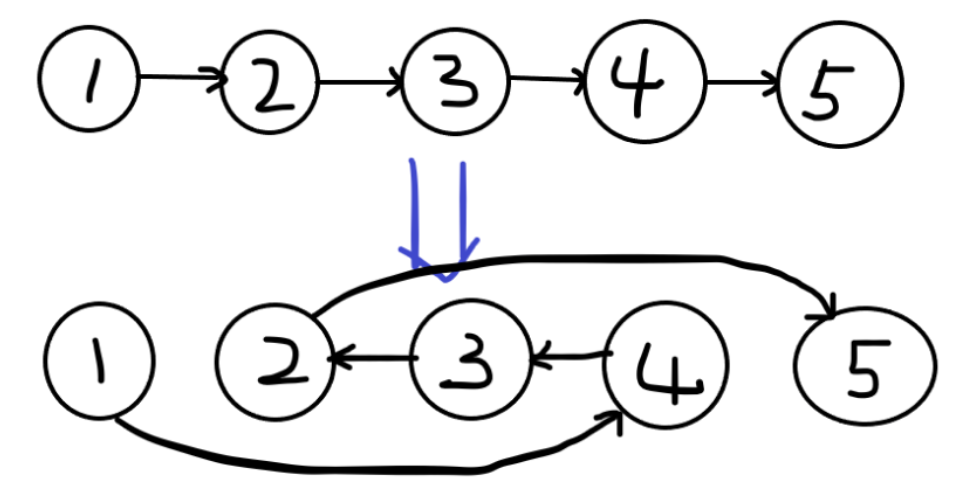
可以看到,实际上不需要真的“翻转”,只要适当改变前驱后继就可以满足要求,像上图,翻转 [2,4] 的实质就是:翻转区间第一个元素 (2) 的前驱 (1) 的后继变为翻转区间最后一个元素 (4) ,翻转区间第一个元素 (2) 的后继变为翻转区间最后一个元素 (4) 的后继,中间元素的前驱变后继,后继变前驱。
对于块状链表,每个链表节点内有多个元素,反转后,不仅前驱后继改变,块内元素也要改变访问顺序。可以用一个翻转标记来维护,每次翻转操作,把这个标记异或 1 ,得到这个块的状态。
对于左右零散块,先下传块内翻转标记,处理出要翻转的元素是谁。
这里显然不可以直接暴力 swap ,因为左右段要翻转的元素不一定一样多,如下图:
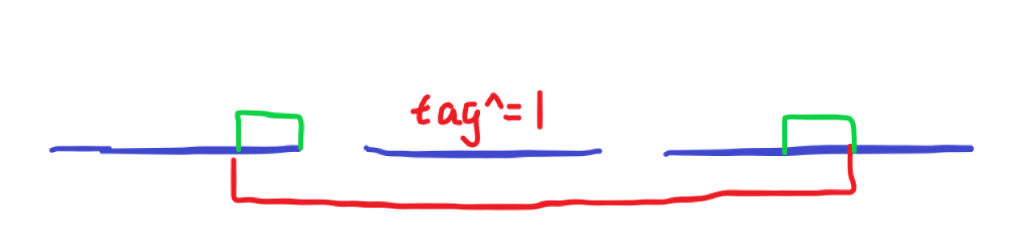
此时如果给中间段整段打 tag 标记的话,由于左右元素不一样多,暴力 swap 之后还需要再进行调整,很麻烦。此时应该下传中间段的标记,调整左右翻转元素的个数,再整体打标记。如下图:
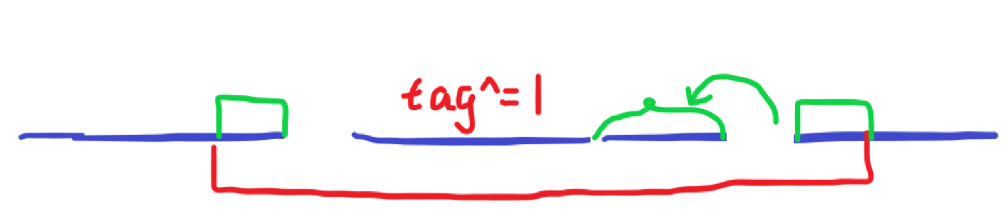
剩下的左右翻转元素数量一样,暴力 swap 即可。
或者直接把所有元素全塞到别的块(也需要先下传标记,否则插入位置不对)里,再整体打标记。如下图:

这里第二种办法实现起来比较简单,不需要讨论左右块中,哪一个块要调整的元素多。(如果采用第一种方法,如果左块翻转元素多,则需要左块后插,右块元素多,则需要右块前插,细节处理较繁琐,并且实测代码比第二种长2.5k。当然另外一种做法是把中间的块里的元素补到零散块里,只是比第一种还要麻烦一些。)
调整完了之后要注意合并、维护块长正确,总复杂度 \(O(\sqrt n)\) 。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
//using namespace std;
const int maxn=200005;
const int maxblock=2005;
int Trashcan[maxn],top,used;
int n,m,tot,len;
struct Node{
int pre,nxt;//前驱后继
int tag;//翻转标记
int lenth;//块长
int a[maxblock];
}Block[maxblock];
inline int read(){
int x=0,fh=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch==‘-‘)
fh=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-‘0‘;
ch=getchar();
}
return x*fh;
}//快读
inline void swap(int &a,int &b){
if(a^b) a^=b^=a^=b;
}//快换
inline void Init(){
n=read(),m=read();
len=sqrt(n);//设定标准块长len
tot=(n-1)/len+1;//设定初始总块数tot
for(int i=1;i<=n;++i){
int belong=(i-1)/len+1;
Block[belong].a[++Block[belong].lenth]=i;//预处理块内元素
}
for(int i=1;i<=tot;++i)
Block[i].pre=i-1,Block[i].nxt=i+1;//链接为链表
Block[tot].nxt=0;
}
inline void reset(int id){//下传id块标记
if(Block[id].tag){
int mid=(Block[id].lenth+1)>>1;
for(int i=1;i<=mid;++i)
swap(Block[id].a[i],Block[id].a[Block[id].lenth+1-i]);
Block[id].tag=0;
}
}
inline void clear(int id){//彻底清除、回收id块
Trashcan[++top]=id;
Block[id].lenth=Block[id].nxt=Block[id].pre=Block[id].tag=0;
memset(Block[id].a,0,sizeof Block[id].a);
}
inline void build(const int id){//在id后面新建一个块
int ip;
if(used<top) ip=Trashcan[++used];
else ip=++tot;
Block[ip].nxt=Block[id].nxt;
Block[Block[id].nxt].pre=ip;
Block[id].nxt=ip;
Block[ip].pre=id;
}
inline void merge(int id){//合并id和其后面的块
int ip=Block[id].nxt;
reset(id);reset(ip);
for(int i=1;i<=Block[ip].lenth;++i)
Block[id].a[i+Block[id].lenth]=Block[ip].a[i];
Block[id].lenth+=Block[ip].lenth;
Block[id].nxt=Block[ip].nxt;
Block[Block[id].nxt].pre=id;
clear(ip);
}
inline void split(int id){//分裂id块
reset(id);build(id);
int ip=Block[id].nxt;
for(int i=len+1;i<=Block[id].lenth;++i)
Block[ip].a[i-len]=Block[id].a[i];
Block[ip].lenth=Block[id].lenth-len;
Block[id].lenth=len;
}
inline void Print(){//遍历链表,输出答案
for(int i=1;i!=0;i=Block[i].nxt){
if(!Block[i].tag)
for(int j=1;j<=Block[i].lenth;++j)
printf("%d ",Block[i].a[j]);
else
for(int j=Block[i].lenth;j>=1;--j)
printf("%d ",Block[i].a[j]);
}
}
int belongL,belongR;
inline void Getpoistion(int &l,int &r){//找到l,r的位置
belongL=1,belongR=1;
while(l>Block[belongL].lenth){
l-=Block[belongL].lenth,r-=Block[belongL].lenth;
belongL=belongR=Block[belongL].nxt;
}
while(r>Block[belongR].lenth){
r-=Block[belongR].lenth;
belongR=Block[belongR].nxt;
}
}
inline void reverse(int l,int r){//最重要的翻转操作
Getpoistion(l,r);
if(belongL==belongR){//在同一段内,直接暴力
reset(belongL);
int mid=(l+r)>>1;
for(int i=l,j=r;i<=mid;++i,--j)
swap(Block[belongL].a[i],Block[belongL].a[j]);
return;
}else{
reset(belongL);reset(belongR);//下传零散段标记
if(Block[belongL].nxt==belongR)
//如果l所处段后继为r所处段,不能直接往中间段塞元素(因为它不存在)要先新建一个
build(belongL);
int revL=Block[belongL].lenth-l+1;//左端零散翻转元素数量
int Nxt=Block[belongL].nxt;
int Pre=Block[belongR].pre;
reset(Nxt);reset(Pre);//找到即将被塞进元素的块,下传他们的标记
for(int i=Block[Nxt].lenth;i>=1;--i)
Block[Nxt].a[i+revL]=Block[Nxt].a[i];
for(int i=l,j=1;i<=Block[belongL].lenth;++i,++j)
Block[Nxt].a[j]=Block[belongL].a[i];//左端往后塞零散元素
Block[belongL].lenth-=revL;
Block[Nxt].lenth+=revL;//重新处理段长
for(int i=Block[Pre].lenth+1,j=1;j<=r;++i,++j)
Block[Pre].a[i]=Block[belongR].a[j];
for(int i=1;i<=Block[belongR].lenth;++i)
Block[belongR].a[i]=Block[belongR].a[i+r];//右端往前塞零散元素
Block[Pre].lenth+=r;
Block[belongR].lenth-=r;//重新处理段长
for(int i=Block[belongL].nxt;i!=belongR;i=Block[i].pre)
swap(Block[i].pre,Block[i].nxt),Block[i].tag^=1;//改变前驱后继,整体标记
swap(Block[belongL].nxt,Block[belongR].pre);
Block[Block[belongL].nxt].pre=belongL;
Block[Block[belongR].pre].nxt=belongR;
if(Block[Nxt].lenth>(len<<1)) split(Nxt);
if(Block[Pre].lenth>(len<<1)) split(Pre);
if(Block[belongL].lenth+Block[Block[belongL].pre].lenth<len && Block[belongL].pre) merge(Block[belongL].pre);
if(Block[belongR].lenth+Block[Block[belongR].nxt].lenth<len && Block[belongR].nxt) merge(belongR);//及时分裂、合并维护块长大约为len
}
}
signed main(){
Init();
while(m--){
int L=read(),R=read();
reverse(L,R);
}
Print();
return 0;
}
块状链表不仅是链表,还是分块!
它在变成一棵文艺平衡树的同时,并没有失去分块的性质。也就是说,它依旧可以维护序列中的问题,再换句话说,在某种情况下,它可以完美的替代掉文艺平衡树,譬如下面这道题目:
题目中要求支持翻转、区间加、区间最大值,翻转操作显然可以用上述的文艺分块术解决。
区间加是分块的基本操作,需要在块内维护一个 add 标记。区间最大值可以通过 \(O(\sqrt n)\) 遍历块提前预处理求出,每次区间加 \(v\) 的时候,最大值也加 \(v\) , 而整块翻转操作显然对这两个标记没有影响。
对于零散块,要把翻转标记和 add 标记都下传,然后再交换对应块元素或者往中间块塞元素。交换后,不管是被塞进元素的块还是往外塞元素的块,都要重新遍历块统计最大值,因为这个最大值可能在这个过程中被交换掉。
这里给出在上面分析原理时提到的第一种方法的代码,另外,介于分块文艺术的代码上面已经有详细介绍了,这里不再给出代码注释。(别的就是分块维护 add 标记什么的不是很简单?好叭其实是我懒)
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
//using namespace std;
inline int read(){
int x=0,fh=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch==‘-‘)
fh=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-‘0‘;
ch=getchar();
}
return fh*x;
}
const int maxn=100005;
#define inf 0x3f3f3f3f
int n,m,tot,len;
int Trashcan[maxn],top,used;
struct Node{
int a[2005];
int pre,nxt;//前驱、后继
int lenth;//长度
int tag;//反转标记
int add;//增量标记
int maxmum;//区间最大值
}Block[2005];
inline void swap(int &a,int &b){
if(a^b) a^=b^=a^=b;
}
inline void reset(const int id){//下传标记
if(Block[id].tag==1){
int mid=(Block[id].lenth+1)>>1;
for(int i=1,j=Block[id].lenth;i<=mid;++i,--j)
swap(Block[id].a[i],Block[id].a[j]);
Block[id].tag=0;
}
for(int i=1;i<=Block[id].lenth;++i)
Block[id].a[i]+=Block[id].add;
Block[id].add=0;
}
inline void update(const int id){//在没有add标记时,重新计算最大值
Block[id].maxmum=-inf;
for(int i=1;i<=Block[id].lenth;++i)
Block[id].maxmum=std::max(Block[id].maxmum,Block[id].a[i]);
}
inline void clear(const int id){//删除编号为id的块
Trashcan[++top]=id;
memset(Block[id].a,0,sizeof Block[id].a);
Block[id].lenth=0;
Block[id].pre=Block[id].nxt=0;
Block[id].tag=0;
Block[id].maxmum=0;
Block[id].add=0;
}
inline void Build(const int id){//在id后面新建一个块
int ip;
if(used<top) ip=Trashcan[++used];
else ip=++tot;
Block[ip].nxt=Block[id].nxt;
Block[Block[ip].nxt].pre=ip;
Block[ip].pre=id;
Block[id].nxt=ip;
}
inline void Delete(const int id){//删除编号为id的块
int Nxt=Block[id].nxt;
int Pre=Block[id].pre;
Block[Pre].nxt=Nxt;
Block[Nxt].pre=Pre;
clear(id);
}
int belongL,belongR;
inline void Getpoisition(int &l,int &r){
belongL=belongR=1;
while(l>Block[belongL].lenth){
l-=Block[belongL].lenth,r-=Block[belongL].lenth;
belongL=belongR=Block[belongL].nxt;
}
while(r>Block[belongR].lenth){
r-=Block[belongR].lenth;
belongR=Block[belongR].nxt;
}
}
inline void split(const int id){
Build(id);reset(id);
int ip=Block[id].nxt;
for(int i=len+1;i<=Block[id].lenth;++i)
Block[ip].a[i-len]=Block[id].a[i];
Block[ip].lenth=Block[id].lenth-len;
Block[id].lenth=len;
update(id);update(ip);
}
inline void merge(const int id){
int ip=Block[id].nxt;
reset(id);reset(ip);
for(int i=Block[id].lenth+1,j=1;j<=Block[ip].lenth;++i,++j)
Block[id].a[i]=Block[ip].a[j];
Block[id].lenth+=Block[ip].lenth;
update(id);Delete(ip);
}
inline void Add(int l,int r,const int v){
Getpoisition(l,r);
if(belongL==belongR){
reset(belongL);
for(int i=l;i<=r;i++)
Block[belongL].a[i]+=v;
update(belongL);
}else{
reset(belongL);
for(int i=l;i<=Block[belongL].lenth;++i)
Block[belongL].a[i]+=v;
update(belongL);
for(int i=Block[belongL].nxt;i!=belongR;i=Block[i].nxt)
Block[i].add+=v,Block[i].maxmum+=v;
reset(belongR);
for(int i=1;i<=r;++i)
Block[belongR].a[i]+=v;
update(belongR);
}
}
inline int Getmax(int l,int r){
int max=-inf;
Getpoisition(l,r);
if(belongL==belongR){
reset(belongL);
for(int i=l;i<=r;++i)
max=std::max(max,Block[belongL].a[i]);
}else{
reset(belongL);
for(int i=l;i<=Block[belongL].lenth;++i)
max=std::max(max,Block[belongL].a[i]);
for(int i=Block[belongL].nxt;i!=belongR;i=Block[i].nxt)
max=std::max(max,Block[i].maxmum);
reset(belongR);
for(int i=1;i<=r;i++)
max=std::max(max,Block[belongR].a[i]);
}
return max;
}
inline void reverse(int l,int r){
Getpoisition(l,r);
if(belongL==belongR){
reset(belongL);
int mid=(l+r)>>1;
for(int i=l,j=r;i<=mid;++i,--j)
swap(Block[belongL].a[i],Block[belongR].a[j]);
return;
}else{
reset(belongL);reset(belongR);
int revL=Block[belongL].lenth+1-l;
if(revL==r){
for(int i=l,j=r;i<=Block[belongL].lenth;++i,--j)
swap(Block[belongL].a[i],Block[belongR].a[j]);
update(belongL);update(belongR);
}else if(Block[belongL].nxt!=belongR){
if(revL>r){
int tmp=revL-r;
int Nxt=Block[belongL].nxt;
reset(Nxt);
for(int i=Block[Nxt].lenth;i>=1;--i)
Block[Nxt].a[i+tmp]=Block[Nxt].a[i];
for(int i=Block[belongL].lenth-tmp+1,j=1;j<=tmp;++i,++j)
Block[Nxt].a[j]=Block[belongL].a[i];
Block[Nxt].lenth+=tmp;
Block[belongL].lenth-=tmp;
update(Nxt);
for(int i=l,j=r;i<=Block[belongL].lenth;++i,--j)
swap(Block[belongL].a[i],Block[belongR].a[j]);
update(belongL);update(belongR);
}else{
int tmp=r-revL;
int Pre=Block[belongR].pre;
reset(Pre);
for(int i=Block[Pre].lenth+1,j=1;j<=tmp;++i,++j)
Block[Pre].a[i]=Block[belongR].a[j];
for(int i=1;i<=Block[belongR].lenth;++i)
Block[belongR].a[i]=Block[belongR].a[i+tmp];
Block[Pre].lenth+=tmp;
Block[belongR].lenth-=tmp;
update(Pre);
for(int i=Block[belongL].lenth,j=1;i>=l;--i,++j)
swap(Block[belongL].a[i],Block[belongR].a[j]);
update(belongL);update(belongR);
}
}else{
if(revL>r){
for(int i=r,j=l;i>=1;--i,++j)
swap(Block[belongL].a[j],Block[belongR].a[i]);
int mid=(l+r+Block[belongL].lenth)>>1;
for(int i=l+r,j=Block[belongL].lenth;i<=mid;++i,--j)
swap(Block[belongL].a[i],Block[belongL].a[j]);
update(belongL);update(belongR);
}else{
for(int i=l,j=r;i<=Block[belongL].lenth;++i,--j)
swap(Block[belongL].a[i],Block[belongR].a[j]);
int mid=(r-revL+1)>>1;
for(int i=1,j=r-revL;i<=mid;++i,--j)
swap(Block[belongR].a[i],Block[belongR].a[j]);
update(belongL);update(belongR);
}
}
if(Block[belongL].nxt!=belongR){//puts("QWQ");
for(int i=Block[belongL].nxt;i!=belongR;i=Block[i].pre)
swap(Block[i].pre,Block[i].nxt),Block[i].tag^=1;
swap(Block[belongL].nxt,Block[belongR].pre);
Block[Block[belongL].nxt].pre=belongL;
Block[Block[belongR].pre].nxt=belongR;
}
if(Block[Block[belongL].nxt].lenth>(len<<1)) split(Block[belongL].nxt);
if(Block[Block[belongR].pre].lenth>(len<<1)) split(Block[belongR].pre);
if(Block[belongL].lenth+Block[Block[belongL].nxt].lenth<len) merge(belongL);
if(Block[belongR].lenth+Block[Block[belongR].nxt].lenth<len && Block[belongR].nxt) merge(belongR);
}
}
inline void Init(){
n=read(),m=read();
len=sqrt(n);
tot=(n-1)/len+1;
for(int i=1;i<=n;++i){
int belong=(i-1)/len+1;
Block[belong].a[++Block[belong].lenth]=0;
}
for(int i=1;i<=tot;++i)
Block[i].pre=i-1,Block[i].nxt=i+1;
Block[tot].nxt=0;
}
inline void Print(){
for(int i=1;i!=0;i=Block[i].nxt){
reset(i);
for(int j=1;j<=Block[i].lenth;++j)
printf("%d ",Block[i].a[j]);
}
puts("");
}
signed main(){
// freopen("1.in","r",stdin);
// freopen("ans.out","w",stdout);
Init();
while(m--){
int opt=read(),l=read(),r=read(),v;
if(opt==1){
v=read();
Add(l,r,v);
}else if(opt==2)
reverse(l,r);
else printf("%d\n",Getmax(l,r));
//Print();
}
return 0;
}
代码略长,仅供娱乐和参考。
标签:原理 art def long put lazy void 长大 区间
原文地址:https://www.cnblogs.com/zaza-zt/p/14939974.html