标签：void   计算   stat   数字   print   无法   loading   方便   没有   

接雨水

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例

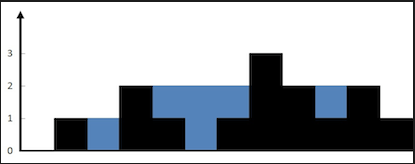
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

分析

1）由上图中中间接到的雨水部分可以看出，从整体来看，是一个凹槽，但分开来看，在高度为1的下方的凹槽被填满后，对于第二层，实际上是形成了新的凹槽，这是由高度差决定的，所以这里需要多重考虑

2）单调栈的使用，这道题涉及到了数组下标和下标对应值的使用，最好的做法就是通过单调栈的方式来寻找凹槽

思路

1）雨水只会在两端都有柱子包围，并且容量以矮的柱子为基准

2）可以分块，方便使用width * height的方式求得某一块的水容量

3）width为数组下标 ，高是求到了两端较为矮的柱子的高度，再减去凹槽处的高度，得到高度差，然后求容水量

4）由于是分块进行的，所以如果此时填满了当前模块的水之后又形成了新的凹槽，那么这时还需要继续执行同理的操作

5）直到不能够装水之后，就往后移动

代码实现

public int trap(int[] height) {
        //储水总量
        int total = 0;
        //定义单调栈
        Stack<Integer> stack = new Stack<>();
        int n = height.length;
        //如果数组长度不超过2无法形成凹槽，所以直接返回0
        if (n <= 2)
            return 0;
        //入栈的是数字下标，是单调递增的，但是对高度需要额外的判断，形成凹槽的条件一定是高度先降低再上升
        for (int i = 0; i < n; ++i) {
            //形成凹槽的判断条件
            while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
                //记下凹槽所在的位置，方便计算凹槽底部所在的高度
                int bottom = stack.pop();
                //如果上升了高度，但左边没有阻挡，也说明了无法形成凹槽，直接停止下面的步骤
                if (stack.isEmpty()) {
                    break;
                }
                //left就是出栈后左侧的高度所在位置
                int left = stack.peek();
                //这里-1是因为两侧都有宽度
                int currWidth = i - left - 1;
                //找到更低一侧的高度，减去凹槽的高度
                int currHeight = Math.min(height[left], height[i]) - height[bottom];
                //加入水量
                total += currWidth * currHeight;
            }
            stack.push(i);
        }
        return total;
    }

测试用例

这里使用的数组就是上图所述的模型

public static void main(String[] args) {
    int[] height = {0,1,0,2,1,0,1,3,2,1,2,1};
    System.out.println(new Trap().trap(height));
}

结果分析

这里的6是由1+1+3+1构成的，符合分析

接雨水

标签：void   计算   stat   数字   print   无法   loading   方便   没有   

原文地址：https://www.cnblogs.com/we1yu4n/p/14941699.html