标签:最低要求 方向 mini 因此 span tar 不完全 图片 font
在机械设计中,根据零件的何种功能要求,对零件的重要几何尺寸,需要同时给定尺寸公差、形位公差等,确定尺寸公差与形位公差之间相互关系的原则成为公差原则。公差原则又分为独立原则和相关要求(各种原则可以去查看上一篇文章
https://www.cnblogs.com/yantingguo/p/14932720.html
其中,相关要求又包含包容要求、最大实体要求、最小实体要求、可逆要求等(也在上一篇文章中介绍)。在机械设计中正确运用公差原则,是对设计者的基本要去,因此我们必须熟悉公差原则的各项基本内容。
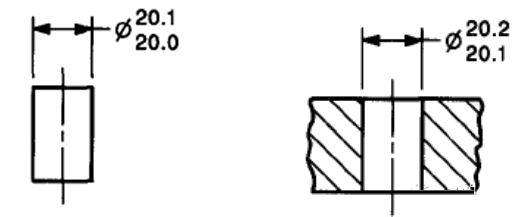
上面的例子是一根轴和一个孔的装配,我们看到孔和轴的MMC都是20.1,根据公差原则,MMC时孔和轴都不允许变形,因此它保证最小间隙为0的装配关系。
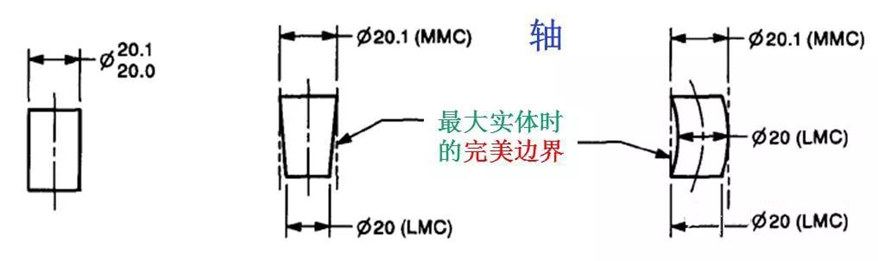
上图描述了轴满足尺寸要求的两种极限状态。轴的MMC边界(20.1)没有被突破,而轴的每个截面的尺寸都满足LMC的要求。
根据这个解释,我们应该怎样去测量这根轴的尺寸呢?简单地用卡尺来测量每个截面是不完全的,简单地用环规来作通止规也是不准确的。
首先我们知道MMC的边界的不允许被突破的,因此我们可以根据MMC的边界来制作一个孔作为通规,通规的深度必须超过轴的长度,如果轴的整个长度能进入通规,那就说明MMC边界没被突破。
其次我们要求每个截面都满足LMC的要求,因此我们可以根据LMC的尺寸来制作一个止规,但考虑到每个截面都要测量,环规是不能满足要求的,所以此时的止规只能是两点或三点的卡规。只有当零件能整个进入通规,并且每个截面都被止规止住,这样才能说零件是合格的。当然此时的卡规也可以用卡尺测量来代替。孔的解释与轴相同,这里就不再赘述了。
总之,评判一个尺寸形体是否满足尺寸要求的依据有两点:
1. 是否通过以MMC边界尺寸制作的通规;
2. 是否每个截面都满足LMC要求。
在LMC时具有完美形状的要求不是默认的。因此当尺寸形体在LMC时,允许有偏离LMC边界的形状误差,最大的形状误差由MMC的完美边界决定。这个从上面的例子中就可以看到了。只有当形位公差用LMC修正时,才要求尺寸形体在LMC时具有完美形状。
MMC和LMC对形位公差的影响
1. MMC及LMC的实际意义
如前所述,零件MMC的状态定义了零件的最小装配间隙(最小的孔减去最大的轴),同时根据公差原则1,确定了MMC边界是不允许被突破的,从而保证了最小装配间隙不会因形状误差而变小。
因此我们说MMC的实际意义是确保了零件的装配。
那么LMC的实际意义是什么呢?我们知道LMC时孔最大,轴最小,这个时候我们考虑的不是孔与轴的装配,而是确保了在轴上打孔时的一个最小壁厚。
如下图所示,孔的LMC是10.5,轴的LMC是14.5,它保证了最小壁厚为(14.5-10.5)/2=2。当然这里的前提是不考虑形状,方向和位置的误差
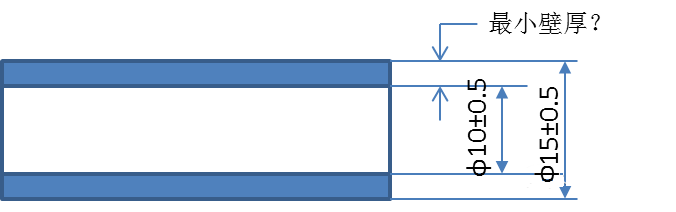
理解MMC及LMC的实际意义对于帮助我们理解在下面的边界条件有很大帮助。无论什么时候,当你看到MMC或MMB符号,那么我们就应该从保证最小装配间隙的角度去理解;当你看到LMC或LMB符号,就应该从保证最小壁厚的角度去考虑。尽管在实际应用中它们可能用于其它目的,但这种理解方法永远是正确的。
顺便提一下RFS – Regardless of Feature Size,翻译过来就是与形体尺寸无关。以前我们称这种状态为公差原则2,即独立原则,图纸上圆圈中的S符号?来表示。现在这个原则已经是一个默认的公理了,因此图上不再有任何符号。当我们在形位公差后没有看到MMC或LMC符号时,它就是RFS。
它表示形体的形位公差与形体的尺寸没有关系,应该分别满足。换句话说就是,无论被测形体的实际尺寸是多少,要求的形位公差值永远是由形位公差框格定义的公差值。
当RFS时,由于它的形位公差是固定的,不会随着尺寸的变化而变化,也就是说,无论孔和轴的实际尺寸是多少,但它们中心的位置要求都是不变的,因此它实际上是保证了孔的中心对轴的中心的距离。
2. MMC对形位公差的影响
当形位公差用MMC修正时,它表达了两个意思:
a. 给定的形位公差值是指被测形体的非关联实际包容体(UAME)在MMC时允许的形位公差。
b. 当被测形体的UAME偏离MMC时,可对形位公差补偿额外的公差。补偿量就等于UAME与MMC的差值(即偏离量)。
不要问为什么,这与公差原则1一样是一个定理。但我们还是可以从装配的角度来理解它。前面提到MMC是考虑满足装配的最低要求,孔越小,轴越大,就越难装配。
下例中,孔在MMC(φ30.1)时允许有φ0.1的位置度公差,这样它们共同定义了一个φ30边界,这个边界是允许轴通过的一个最小边界。那么当孔的实际尺寸比MMC大时,是否就可以允许孔的位置更偏一点?我们讲只要这个φ30边界不被突破,装配条件就能被满足。因此说孔越大,它的位置就允许偏得越多,也就说它允许的位置度公差就越大。
同样的道理,轴的实际尺寸越小,它所允许的位置度公差就越大。因此它们的位置公差就得到了补偿,而这个补偿量就是实际尺寸(UAME)偏离MMC的偏离量,这样就能保证由实际尺寸和在这个尺寸下的位置度公差定义的边界是一致,也就保证了它的可装配性。下图显示了孔和轴在各种实际尺寸时允许的位置度公差。
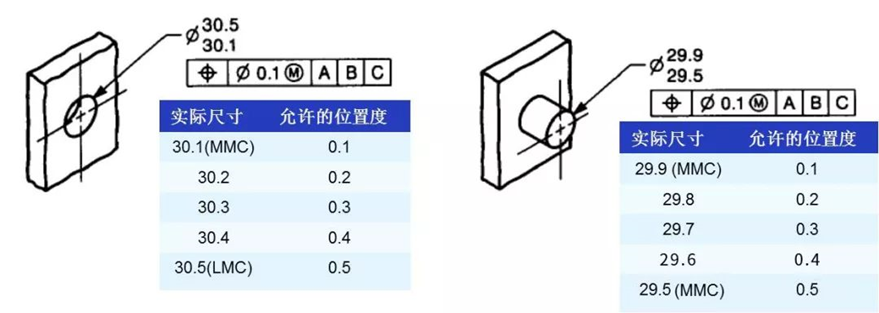
我们可以看到,对孔来说,实际尺寸减去位置度公差定义的一个最差装配边界在不同的实际尺寸时都是φ30,是一致的。同样,对轴来说,实际尺寸加上位置度公差定义的一个最差装配边界在不同的实际尺寸时也都是φ30,也是一致的。
3. LMC对形位公差的影响
当形位公差用LMC修正时,它也表达了两个意思:
a. 给定的形位公差值是指被测形体的非关联实际最小材料包容体(Unrelated
Actual Minimal Material Envelope - UAMME)在LMC时允许的形位公差。
b. 当被测形体的UAMME偏离LMC时,可对定位公差补偿额外的公差。补偿量等于UAMME与LMC的差值(即偏离量)。
同样它也是一个定理。前面我们讲过,LMC是用保证一个最小的壁厚,孔越大,轴越小,壁厚就越小。
下例中,孔在LMC(φ20)时允许有φ0.25的位置度公差,这样它们共同定义了一个φ20.25的最大边界,这个边界是设计要求满足最小壁厚的一个最差边界。那么当孔的实际尺寸比LMC小时,是否就允许孔的位置更偏一点?我们讲只要这个φ20.25的最大边界不被突破,最小壁厚要求就能被满足。所以说孔的实际尺寸越小,它的位置就允许偏得越多,也就说它允许的位置度公差就越大。
同样的道理,轴的实际尺寸越大,它所允许的位置度公差就越大。因此它们的位置公差就得到了补偿,而这个补偿量就是实际尺寸偏离LMC的偏离量,这样就能保证由实际尺寸和在这个尺寸下的位置度公差定义的边界是一致,也就保证了它的最小壁厚要求。
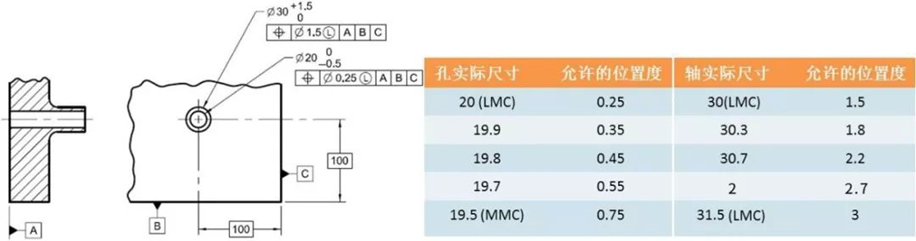
我们可以看到,对孔来说,实际尺寸加上位置度公差定义的一个形成最小壁厚的最差边界在不同的实际尺寸时都是一致的(20.25)。同样,对轴来说,实际尺寸减去位置度公差定义的一个形成最小壁厚的最差边界在不同的实际尺寸时也都是一致的(28.5)。这样就保证了设计最小壁厚为(28.5-20.25)/2=3.125。
标签:最低要求 方向 mini 因此 span tar 不完全 图片 font
原文地址:https://www.cnblogs.com/yantingguo/p/14941684.html