002 数电 (2) : 逻辑代数

标签：inf   数字   运算   结果   逻辑状态   org   取反   有一个   就是   

一、基本概念

• 逻辑：是指事物间的因果关系
• 二值逻辑：是指两种对立逻辑状态的逻辑关系。
• 逻辑代数：1849年英国数学家乔治，布尔( George Boole)首先提出了进行逻辑运算的数学方法————布尔代数。后来，由于布尔代数被广泛应用于解决开关电路和数字逻辑电路的分析与设计中，所以也将布尔代数称为开关代数或逻辑代数。逻辑代数就是布尔代数在二值逻辑电路中的应用。
• 逻辑变量：逻辑代数中的变量，常用字母表示。

二、逻辑代数基本运算

三、基本公式和常用公式

 　　特别注意摩根定律，总结起来就是变量（或变量组）取反，符号乘加互换，总体再加个反号，例如：

四、基本定理

1、代入定理：在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，则等式仍然成立。

2、反演定理：逻辑式 Y，其对偶式结果为 Y‘。

• ①先括号、然后乘、最后加。
• ②非单变量的反号应保留不变。

3、对偶定理：两逻辑式相等，则其对偶式也相等。

• 对偶式Y^D： · 和 + 互换，0 和 1 互换

五、逻辑函数及其表示方法

1.逻辑真值表

2.逻辑函数式

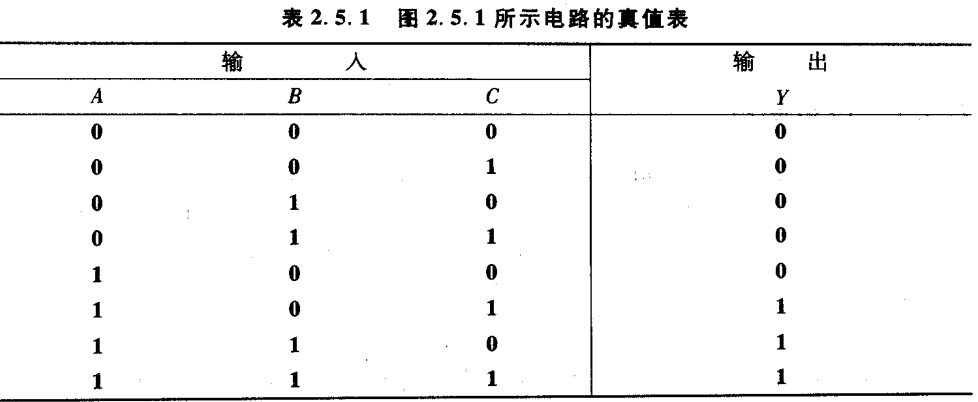
Y=A(B+C)

3.逻辑图

4.波形图

六、波形图

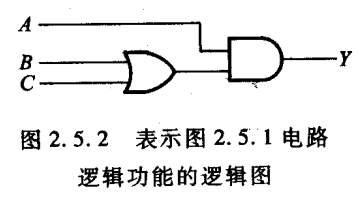
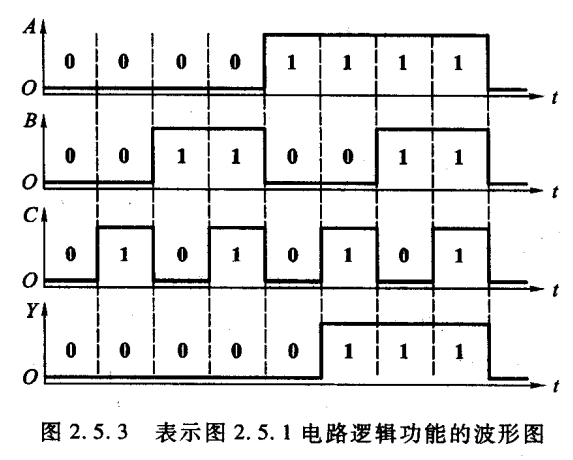
　　如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列起来,就得到了表示该逻辑函数的波形图。这种波形图(waveform)也称为时序图( timing diagram)。

例如：Y = A（B+C）的波形图如下所示：

　　仔细观察一下发现，将这个波形图逆时针旋转90度，或者脑袋横着看，就是真值表！那么波形图化函数式也就成了真值表化函数式：

• ①找出真值表中使逻辑函数 Y=1 的那些输人变量取值的组合。
• ②每组输人变量取值的组合对应一个乘积项，其中取值为1的写人原变量，取值为 0 的写人反变量。
• ③将这些乘积项相加，即得 Y 的逻辑函数式。

七、最小项和最大项（扫一眼即可）

1、最小项

①定义：

　　n个因子的乘积项中，每个因子均以原变量或反变量出现一次。

②例子：

　　A、B、C 的乘积项的最小项有：A‘B‘C‘、A‘B‘C、A‘BC‘、A‘BC、AB‘C‘、AB‘C、ABC‘、ABC。（类似三-八译码器）编号如下所示：

 ③性质：

• n个变量有 2ⁿ 个最小项。
• 所有最小项之和为 1。
• 任意两个最小项之积为 0。
• 相邻性的两个最小项之和可以合并。相邻性：即两个最小项只有一个因子不同。

④最小项之和：

　　逻辑函数式化为“积之和”（与或）的形式。

2、最大项

　　最小项是与，即相乘之积，而最大项是或，即相加之和。

• n个变量有 2ⁿ 个最大项。
• 所有最大项之积为 0。
• 任意两个最大项之和为 1。
• 相邻性的两个最小项之和可以合并。
• 最大项 = 最小项取反，即 M_i = m_i‘。

　　最大项之和：逻辑函数式化为“和之积”（或与）的形式。

八、卡诺图化简法（化简结果不唯一）

1、表示方法

（1）释义

　　将 n 变量的全部最小项各用一个小方块表示，并使具有逻辑相邻性的最小项在几何位置上也相邻地排列起来，所得到的图形称为 n 变量最小项的卡诺图。

（2）卡诺图

 （3）说明

　　①不是按自然二进制排列的，而是 2、3 互换，目的是保证逻辑相邻性。（其实就是格雷码排列）

　　②任何一行或一列，两端之间也有逻辑相邻性。

　　③轴变量 ≥ 3 后需要中间轴对称，前半边首位为0，剩余位照旧，后半边首位为1，剩余位和左半边轴对称。（其实就是格雷码排列）

（4）技巧

　　不一定要化成最小项之和，例如 Y = AC‘ + B，对于 AC‘ ，直接将所有 A=1，C=0的位置填 1 即可；对于 B，直接将所有 B=1 的位置填 1 即可。

2、卡诺图化简——圈 1 法

　　具有相邻性的最小项（即1）合并，并消去不同的因子。注意，只能以 2ⁿ 为圈，可以单排、单列圈，也可以矩形圈。

　　例如：用卡诺图化简法将 Y = AC‘+A‘C+BC‘+B‘C 化简为最简与或函数式。

　　首先画出其卡诺图，，然后画圈圈，有 2 种画圈圈的方案：

 　　对于圈圈(a)：Y=AB‘+A‘C+BC‘

　　 对于圈圈(b)：Y=AC‘+B‘C+A‘B

3、卡诺图化简——圈 0 法

　　圈 0 法的做法和圈 1 法完全一致，只是圈的目标是 0，而结果等于 Y‘，对 Y‘ 再取反即得到答案 Y。

　　圈 0 法对于 1 多 0 少 的卡诺图偶尔有奇效。

九、无关项化简（出题少）

1、无关项

　　分为约束项和任意项，是否把这些最小项写入函数式无关紧要。

（1）约束项

　　对输入变量取值的限制称为约束。当限制某些输入变量的取值不能出现时，用对应的最小项等于 0 表示，这些最小项就是约束项，例如：

（2）任意项

　　输入变量是 1 或 0 皆可，并不影响电路的功能，用对应的最小项等于 1 表示，这些最小项就是任意项。

2、无关项的卡诺图化简

（1）要求

• 无关项在函数式中用 d(...）表示，在卡诺图中用 × 表示。
• 无关项与函数式尽可能多的最小项具有逻辑相邻性。
• 合并时，把 × 作为 1 或 0，应以得到的相邻最小项组合最大、数目最少为原则。

（2）例题

　　解：Y = A‘D + AD‘

参考资料：

1.阎石. 数字电子技术基础(第5版)[M]. 高等教育出版社, 2006.

2.https://www.cnblogs.com/xianyufpga/

002 数电 (2) : 逻辑代数

标签：inf   数字   运算   结果   逻辑状态   org   取反   有一个   就是   

原文地址：https://www.cnblogs.com/linford/p/14966171.html