codeforces 498D Unbearable Controversy of Being (暴力乱搞)

标签：style   http   io   ar   color   os   sp   for   on   

传送门：点击打开链接

题目大意：

定义下图为“damn rhombus”，给定一个有向图，求出有多少个“damn rhombus”。

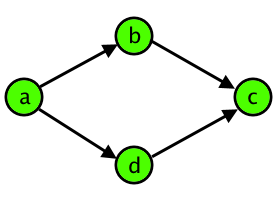
解题思路1：

分析可以得出其实“damn rhombus”的意思就是求a->c通过2个节点中转的个数。也就是说 如果a->c中间中转了x个点，那么对于点对(a,c)来说“damn rhombus”就有C（x,2）个。

那么通过层数为2的bfs就可以得出答案。

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
#define INF 0x7f7f7f7f
#define maxn 3010
#define maxm 30010
using namespace std;
struct Edge
{
    int to;
    int next;
}es[maxm];
int cnt,p[maxn];
int used[maxn];
int n,m;

void add(int x,int y)
{
    es[cnt].to = y;
    es[cnt].next = p[x];
    p[x] = cnt++;

}
long long bfs(int x)
{
    memset(used,0,sizeof used);
    queue <int > q;
    for(int i = p[x];i+1;i = es[i].next)
     q.push(es[i].to);
    while(!q.empty())
    {
        int t = q.front();
        q.pop();
        for(int i = p[t];i+1;i = es[i].next)
        if(es[i].to != x) used[es[i].to]++;
    }
    long long res = 0;
    for(int i = 1;i <= n;i++) if(used[i] >= 2) res += (used[i]-1)*used[i]/2;
    return res;
}

int main()
{
    scanf("%d %d",&n,&m);

    memset(p,-1,sizeof p);
    for(int i = 0;i < m;i++)
    {
        int x,y;
        scanf("%d %d",&x,&y);
        add(x,y);
    }
    long long ans = 0;
    for(int i = 1;i <= n;i++)
    {
        ans += bfs(i);
    }
    printf("%d\n",ans);

    return 0;
}

我在比赛的时候想到了一个很奇葩的做法。虽然被上面的代码skipped了。但是事实上是可以过的。悲伤的表情。

构造矩阵A。 A[i][j]表示从i->j不经过中转的路径数目。

那么学过线性代数的都知道，这个矩阵自乘的结果其实就是a[i][j]表示i->j经过一次中转的路径条数。只需要加一个优化就居然可以让O(n3)的代码过掉。

真的代码不要太短。

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
long long  a[3010][3010];
long long res[3010][3010];
int n,m;
int main()
{
    scanf("%d %d",&n,&m);
    for(int i = 0;i < m;i++)
    {
        int x,y;
        scanf("%d %d",&x,&y);
        a[x][y]++;
    }
    for(int k = 1;k <= n;k++)
        for(int i = 1;i <= n;i++)
        {
            if(a[i][k] == 0) continue;//优化
            for(int j = 1;j <= n;j++)
                res[i][j] += a[i][k]*a[k][j];
        }
    long long ans = 0;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= n;j++)
        {
            if(i == j) continue;
            ans += (res[i][j]*(res[i][j]-1))/2;
        }
    printf("%d\n",ans);
    return 0;
}

codeforces 498D Unbearable Controversy of Being (暴力乱搞)

标签：style   http   io   ar   color   os   sp   for   on   

原文地址：http://blog.csdn.net/tsxhl111/article/details/41281705