标签:style blog http io ar color os sp on
题意: 给一条线段,和一个矩形,问线段是否与矩形相交或在矩形内。
解法: 判断是否在矩形内,如果不在,判断与四条边是否相交即可。这题让我发现自己的线段相交函数有错误的地方,原来我写的线段相交函数就是单纯做了两次跨立实验,在下图这种情况是错误的:
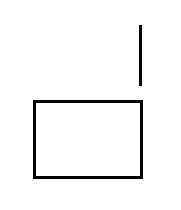
这样的话线段与右边界的两次跨立实验(叉积<=0)都会通过,但是并不相交。
所以要加快速排斥。
还有就是这题题目说给出的不一定是左上角,右下角依次的顺序。所以干脆重新自己定义左上角,右下角。
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> #include <cmath> #include <algorithm> #define eps 1e-8 using namespace std; #define N 100017 struct Point{ double x,y; Point(double x=0, double y=0):x(x),y(y) {} void input() { scanf("%lf%lf",&x,&y); } }; typedef Point Vector; struct Circle{ Point c; double r; Circle(){} Circle(Point c,double r):c(c),r(r) {} Point point(double a) { return Point(c.x + cos(a)*r, c.y + sin(a)*r); } void input() { scanf("%lf%lf%lf",&c.x,&c.y,&r); } }; struct Line{ Point p; Vector v; double ang; Line(){} Line(Point p, Vector v):p(p),v(v) { ang = atan2(v.y,v.x); } Point point(double t) { return Point(p.x + t*v.x, p.y + t*v.y); } bool operator < (const Line &L)const { return ang < L.ang; } }; int dcmp(double x) { if(x < -eps) return -1; if(x > eps) return 1; return 0; } template <class T> T sqr(T x) { return x * x;} Vector operator + (Vector A, Vector B) { return Vector(A.x + B.x, A.y + B.y); } Vector operator - (Vector A, Vector B) { return Vector(A.x - B.x, A.y - B.y); } Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); } Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); } bool operator < (const Point& a, const Point& b) { return a.x < b.x || (a.x == b.x && a.y < b.y); } bool operator >= (const Point& a, const Point& b) { return a.x >= b.x && a.y >= b.y; } bool operator <= (const Point& a, const Point& b) { return a.x <= b.x && a.y <= b.y; } bool operator == (const Point& a, const Point& b) { return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0; } double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; } double Length(Vector A) { return sqrt(Dot(A, A)); } double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); } double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x; } Vector VectorUnit(Vector x){ return x / Length(x);} Vector Normal(Vector x) { return Point(-x.y, x.x) / Length(x);} double angle(Vector v) { return atan2(v.y, v.x); } bool SegmentIntersection(Point A,Point B,Point C,Point D) { return max(A.x,B.x) >= min(C.x,D.x) && max(C.x,D.x) >= min(A.x,B.x) && max(A.y,B.y) >= min(C.y,D.y) && max(C.y,D.y) >= min(A.y,B.y) && dcmp(Cross(C-A,B-A)*Cross(D-A,B-A)) <= 0 && dcmp(Cross(A-C,D-C)*Cross(B-C,D-C)) <= 0; } //data segment struct node{ Point P[2]; }line[206]; //data ends int main() { int T; scanf("%d",&T); while(T--) { double x1,y1,x2,y2; double xleft,ytop,xright,ybottom; Point A,B; A.input(), B.input(); scanf("%lf%lf%lf%lf",&xleft,&ytop,&xright,&ybottom); Point P1,P2,P3,P4; double XL = min(xleft,xright); double XR = max(xleft,xright); double YB = min(ybottom,ytop); double YT = max(ybottom,ytop); xleft = XL, xright = XR, ybottom = YB, ytop = YT; P1 = Point(xleft,ytop); P2 = Point(xleft,ybottom); P3 = Point(xright,ytop); P4 = Point(xright,ybottom); int flag = 0; if(SegmentIntersection(A,B,P1,P3) || SegmentIntersection(A,B,P1,P2) || SegmentIntersection(A,B,P2,P4) || SegmentIntersection(A,B,P3,P4)) flag = 1; if(dcmp(A.x-xleft) >= 0 && dcmp(A.x-xright) <= 0 && dcmp(A.y-ytop) <= 0 && dcmp(A.y-ybottom) >= 0 && dcmp(B.x-xleft) >= 0 && dcmp(B.x-xright) <= 0 && dcmp(B.y-ytop) <= 0 && dcmp(B.y-ybottom) >= 0) flag = 1; if(flag) puts("T"); else puts("F"); } return 0; }
POJ 1410 Intersection --几何,线段相交
标签:style blog http io ar color os sp on
原文地址:http://www.cnblogs.com/whatbeg/p/4109222.html