标签:style blog http io ar os sp 数据 on
逻辑回归(Logistic Regression)是机器学习中十分常用的一种模型,属于广义线性模型。在互联网领域得到了广泛的应用,尤其是在广告系统中用来估计CTR。本文主要介绍逻辑回归的模型形式,求解策略和算法。接着介绍逻辑回归的最大似然估计,最后说明为什么逻辑回归要采用sigmoid函数做变换。
我们知道,线性回归模型输出的是一个连续值,如果我们要输出的不是连续值,该怎么做呢?假设我们的输出只有 1 和 -1。
逻辑回归模型形式上是把线性回归模型做一个变换,让其输出是一个 0 到 1之间的数,假设我们的变换叫做 $g(z) $,然后在变换后的结果上定义一个决策函数,如果:
$\Large y=1 \qquad \text{if} \qquad g(z) > 0.5$
$\Large y=-1 \qquad \text{if} \qquad g(z) < 0.5$
其中 $z$ 就是我们前面讲到的线性模型:
$\Large z = \mathbf{w}^T \mathbf{x} $
而变换采用了逻辑变换,也叫 sigmoid 变换,其形式为:
$\Large g(z) = \frac {1}{1 + e^{-z}} $
通过上面几个式子进行一个简单的推导,我们的决策函数变为:
$\Large y=1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} > 0$
$\Large y=-1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} < 0$
最后我们的逻辑回归模型就变成:
$\Large h_{\mathbf{w}}(\mathbf{x}) = g_{\mathbf{w}}(\mathbf{x}) = \frac {1}{1 + e^{- \mathbf{w}^T \mathbf{x}}} $
我们看看 sigmoid 函数有什么特点,从下面的图形可以看出,这个函数是个连续光滑函数,定义域是 $(-\infty, \infty)$,值域是 $[0,1]$,在 0 附近函数的区分度很高($y$的值变化比较明显),越往两边,函数的区分度就越低($y$的值变化越来越不明显)。
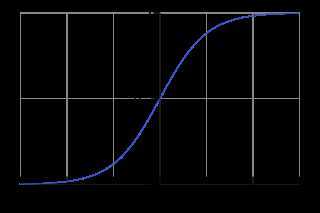
并且这个函数处处可导,其导数为:
$\Large g^\prime = (\frac {1}{1 + e^{-z}})^\prime = \frac {e^{-z}} {(1 + e^{-z})^2} = g(z) \cdot (1- g(z)) $
其导数可以由自己本身表示。
而且:
$\Large g(-z) = \frac {1}{1 + e^z} = 1 - g(z) $
$\Large z=0, e^0=1, g(z) = 1/2 $
$\Large z \to \infty, e^{-\infty} \to 0, g(z) = 1$
$\Large z \to -\infty, e^{\infty} \ to \infty, g(z) = 0$
其实 sigmoid 具备的这些良好性质还不是我们为什么选择它的根本原因,根本原因在后面介绍。
有了逻辑回归模型的形式,我们仍然需要根据我们观测到的数据集求出模型里未知的 $\mathbf{w}$,为此我们仍然采用定义损失函数,并最小化损失函数的策略。此时我们不能用线性回归里采用的平方损失函数,因为此时在逻辑变换的基础上,改函数不再是一个凸函数,会给我们的极小化造成相当大的麻烦。为此,我们定义另外一个损失函数,逻辑斯谛损失(也叫交叉熵 Cross Entropy):
$\Large cost( h_{\mathbf{w}} (\mathbf{x}) ) = -\ln ( g(y (\mathbf{w})^T (\mathbf{x})) ) = -\ln (g(yz))$
我们先看看我们的的决策函数:
$\Large y=1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} > 0$
$\Large y=-1 \qquad \text{if} \qquad z=\mathbf{w}^T \mathbf{x} < 0$
检验一下我们的损失函数:
当 $y=1$时:
$\Large \text{if} \qquad z \to \infty, g(yz) \to 1, cost \to 0$
$\Large \text{if} \qquad z \to -\infty, g(yz) \to 0, cost \to \infty$
当 $y=-1$时:
$\Large \text{if} \qquad z \to \infty, g(yz) \to 0, cost \to \infty$
$\Large \text{if} \qquad z \to -\infty, g(yz) \to 1, cost \to 0$
所以最后我们总的损失函数为:
$\Large L(\mathbf{w}) = -\frac {1}{m} \sum_{i=1}^m \ln ( g(y (\mathbf{w})^T (\mathbf{x})) ) = \frac {1}{m} \sum_{i=1}^m \ln ( 1 + e^{-y^i \mathbf{w}^T \mathbf{x}^i} ) $
我们仍然采用梯度下降来求解 $\mathbf{w}$,因为梯度下降收敛太慢,一般工程上都不会直接采用梯度下降来解这个问题,工程上会采用拟牛顿法比如LBFGS来求解(具体原理请参考),这里为了简单,用梯度下降示例。
先求 $L(\mathbf{w})$ 的梯度向量:
$\Large \nabla (\mathbf{w}) = \frac {1}{m} \sum_{i=1}^m g(-y^i \mathbf{w}^T \mathbf{x}^i )(-y^i \mathbf{x}^i) $
其中 $m$ 为训练数据集的大小。
逐步更新 $\mathbf{w}$:
$\Large \mathbf{w} := \mathbf{w} - \alpha \nabla (\mathbf{w}) $
上面提到了逻辑斯谛损失,为什么我们要定义这样一个损失呢?我们从另一方面来解释,我们假设我们的模型最后分别以一定概率输出 1 和 -1, 假设输出 1 的概率是 $p$, 输出 -1 的概率是 $1-p$,即:
$\Large p(y=1|\mathbf{x}) = p, p(y=-1|\mathbf{x})=1-p $
$p/1-p$ 我们称之为几率,$\ln(\frac {p} {1-p})$ 我们称之为对数几率,我们建立下面这样一个线性模型来模拟这个对数几率:
$\Large \ln(\frac {p} {1-p}) = \mathbf{w}^T \mathbf{x}$
然后很快就能求出:
$\Large p = \frac {1}{1 + e^{-z}} $
其中:
$\Large z = \mathbf{w}^T \mathbf{x} $
下面我们用最大似然估计来估计 $\mathbf{w}$,假设我们的训练数据集为:
$\Large D={(\mathbf{x}^1, y^1),(\mathbf{x}^2, y^2),\ldots,(\mathbf{x}^m, y^m)}$
生成这样一个数据集的概率为:
$\Large p(D) = p(\mathbf{x}^1)p(y^1 | \mathbf{x}^1) p(\mathbf{x}^2)p(y^2 | \mathbf{x}^2) \ldots p(\mathbf{x}^m)p(y^m | \mathbf{x}^m) $
将我们的模型代进去:
// TODO
为什么sigmoid函数比别的非线性函数有吸引力呢?做sigmoid变换的目的是把(-00, +00)的取值范围(用x表示)映射到 (0,1)范围内(用y表示): h = y(x), 为此我们应该选择什么样的 h 呢,h 变换可以理解成对 x 的一种编码,当然h最好是双射,意味着可以从y反解码得到x。理论上满足双射的h可以有无穷多种,该怎么选择呢?实际上双射是不可能的,因为观测 y 时不可避免的要引入误差, 即 y = h(x) +e, 其中 e 为误差,在有误差的情况下,x和y就不是一一映射了。任何从 y 反解码得到 x 都是不可能的,所以问题来了:有没有一种映射h,在有误差的情况下做到最优? 通俗的讲,就是寻找一个映射h,在有观测误差e的情况下,最有的保持输入信号x的信息,用信息学的语言描述就是x与y之间的户信息最大, 而I(x,y)= H(y)- H(y|x)= H(y)- H(e)。x y的户信息由两项决定 H(y)=H(h(x)) 和 H(e),而其中第二项完全由误差决定,我们控制不了。第一项 H(y)是由映射h决定的, H(y)越大越好,所以问题又变成:给定取值范围[0,1],熵 H(y)什么时候最大?答案就是y服从均匀分布时熵最大,因此,能把x映射成一个均匀分布的映射h是最优的。 当知道x的概率密度为f(x)时,怎么样的变换能把 x 变成均匀分布呢?还记得遇到多这样的面试题吗: 如何用0,1的均匀分布生成任意的其他概率分布?答案是用一种叫inverse cumulative distribution function 的变换方法。而这里的问题正好和面试题相反,我们要从任意分布生成均匀分布。答案就是f(x)的累积分布函数F(x)就是最优的h。想象一下正态分布的概率密度函数,是一个倒置的钟形函数,而它的累积分布函数是不是和 sigmoid 函数长得很像?而现实中我们遇到的倒置钟形分布的信号又比比皆是。注意:对概率密度不是倒置钟形的信号,sigmoid变换不一定是最优的。
标签:style blog http io ar os sp 数据 on
原文地址:http://www.cnblogs.com/dudi00/p/4093238.html