标签:style blog http io ar color os 使用 sp
1.引言
在高斯混合和EM算法中,我们运用EM算法拟合混合模型,但是我们得考虑得需要多少的样本数据才能准确识别出数据中的多个高斯模型!看下面两种情况的分析:
这和解多元线性方程组是一样的道理,就是自变量的个数多于非线性相关的方程的个数,这必然导致解的不唯一,虽然在解方程的时候可以随便选一个解满足方程组,但是对于某一实际数据集,往往样本对应的概率分布在客观上都是唯一的,只是我们无法简单地用概率论中的几个典型的分布准确表示出来罢了!
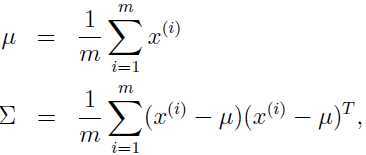
我们会发现,协方差矩阵 Σ 是奇异的,即 Σ 不可逆,Σ-1 不存在,且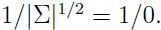 但是这两项在计算多元高斯分布时,又都是必不可少的。
但是这两项在计算多元高斯分布时,又都是必不可少的。
所以,除非 m 比 n 大一定较合适的数值,否则对方差和均值的最大似然估计将会很难找到正确的值。
然而,我们仍然能够拟合出关于数据的合理的高斯分布,并且或许还能挖掘出数据的一些有趣的变化结构。如何做到的呢?
2.对 Σ 的约束
如果没有充足的数据拟合出完全的协方差矩阵,就要对协方差矩阵的空间作出一些限制。
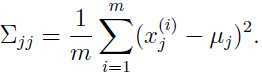
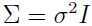 ,其中 I 是单位矩阵,
,其中 I 是单位矩阵,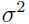 是可以调整元素大小的参数,可以推导出:
是可以调整元素大小的参数,可以推导出: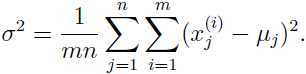
如果拟合数据的一个无约束的,非稀疏的协方差矩阵,为了保证最大似然估计得出的协方差矩阵Σ 非奇异,必须要求 m ≥ n+1.
但是,要求 Σ 是对角矩阵就意味着所有数据样本的坐标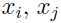 是独立且非相关的(具体原因回顾概率论有关协方差的知识,参考机器学习中有关概率论知识的小结),
是独立且非相关的(具体原因回顾概率论有关协方差的知识,参考机器学习中有关概率论知识的小结),
通常情况下,如果能捕获出数据中内在的一些感兴趣的相关结构就更好了!如果按照上述的两种约束,做不到这一点。
后面会介绍一种因子分析模型(factor analysis model), 将会使用更多参数而不仅仅是协方差矩阵Σ,捕获出数据中的一些关联,同时不用必须拟合一个全协方差矩阵.
3.高斯分布的边缘分布和条件分布
在讨论因子分析模型之前,先回顾下概率论中的一些知识,就是如何求出多元高斯分布的条件分布和边缘分布。
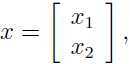
其中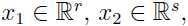
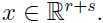 即 x1, x2 都是向量.
即 x1, x2 都是向量.
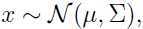 其中:
其中: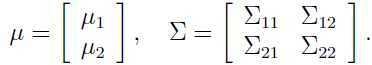
其中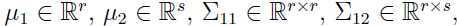 等等。注意由于协方差矩阵式对称矩阵,所以
等等。注意由于协方差矩阵式对称矩阵,所以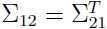
在我们的假设下,x1, x2 服从多元高斯分布,那么什么是x1 的边缘分布呢?
容易看出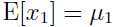 ,
,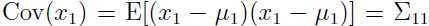
关于 x 的协方差,即 x1, x2 的联合协方差:
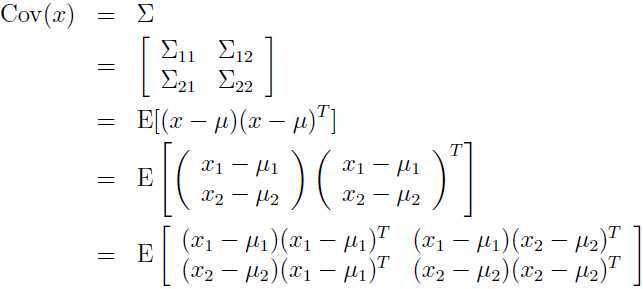
可以看出左上角的分块是与我们计算的 x1 的协方差相一致。
由于高斯分布的边缘分布还是高斯分布,于是 x1 的边缘分(把x2 看成是常量)布写作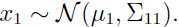
那什么是在给定 x2 时,x1 的条件分布呢?通常被写为: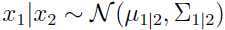 ,其中:
,其中:
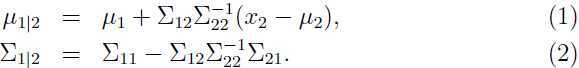
在讨论因此分析模型的时候,这些计算边缘分布和条件分布的式子将会很有用。
4.因子分析模型
在因子分析模型中,假设一个关于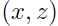 联合分布,其中
联合分布,其中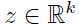 是隐变量:
是隐变量:
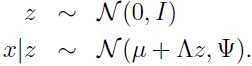
模型中的参数 μ 是向量: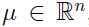 ,矩阵
,矩阵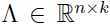 ,矩阵
,矩阵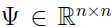 ,k 的取值通常比 n 小.
,k 的取值通常比 n 小.
因此,可以把每一个数据点 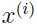 看作是从一个 k 维的多元高斯分布
看作是从一个 k 维的多元高斯分布 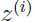 采样得到的.
采样得到的.
可以把上面的因子模型假设等效写成下面的形式:
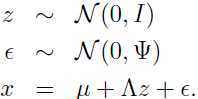
其中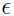 和
和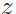 相互独立。
相互独立。
下面看看我们模型到底定义出了什么样的分布。
由上面的式子可以看出,我们的随机变量 z 和 x 服从联合高斯分布 :
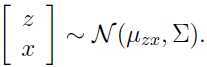
现在来找出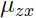 和
和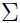 .
.
由上面的条件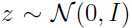 知道:
知道: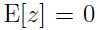 ,所以:
,所以:
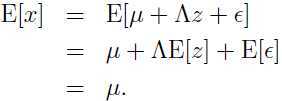
注意上面推理中 矩阵 Λ 不是随机变量,里面的所有元素都是常量,所以 Λ 的期望仍是本身。
因此可以得出:
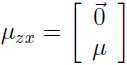
为了得出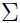 ,需要计算:
,需要计算:
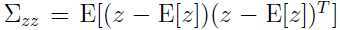
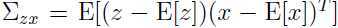
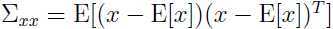
由于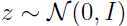 ,所以
,所以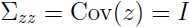
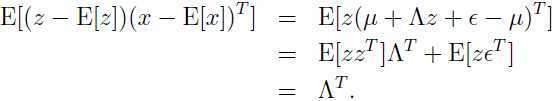
在对后一步中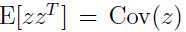 ,
,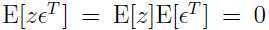
同样有:
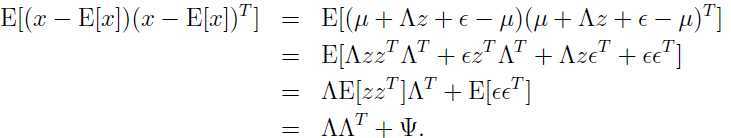
综上所述有:
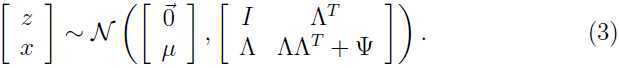
因此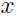 的边缘分布:
的边缘分布: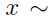
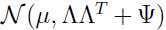
给定一个训练集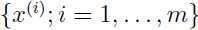 ,那么参数的的对数似然函数为:
,那么参数的的对数似然函数为:
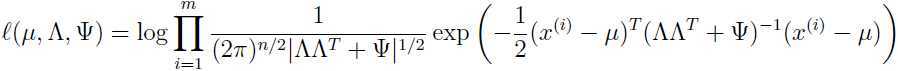
对这个似然函数最大化看上去就很麻烦,确实也很麻烦,但是有稍微简单点的方法,那就是EM算法(EM算法参考EM算法原理详解)
5.EM算法运用于因子分析
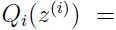
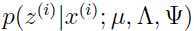
把上面式子(3)的结果代入式子(1)(2),得到:
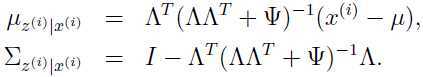
有这两个参数,即数学期望和协方差,可以写出要求的条件高斯分布:
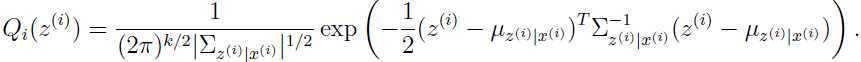
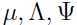 的对数似然函数:
的对数似然函数: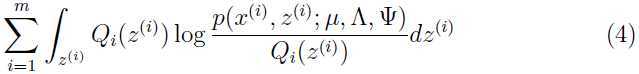
这里以如何优化参数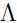 为例详解,首先把上面的式子简化为:
为例详解,首先把上面的式子简化为:
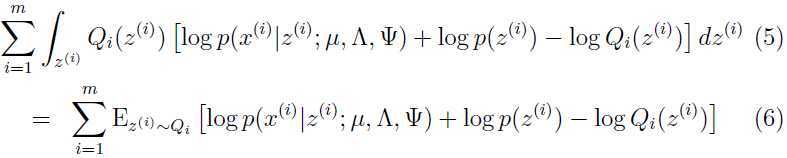
下标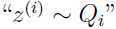 表示
表示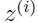 是服从分布
是服从分布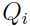 .
.
因为现在要优化参数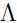 ,所以把与
,所以把与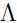 无关的项去掉,因为无关项此时就是常数,没有优化的必要,只需与参数有关的项最大化即可,而我们需要最大化:
无关的项去掉,因为无关项此时就是常数,没有优化的必要,只需与参数有关的项最大化即可,而我们需要最大化:
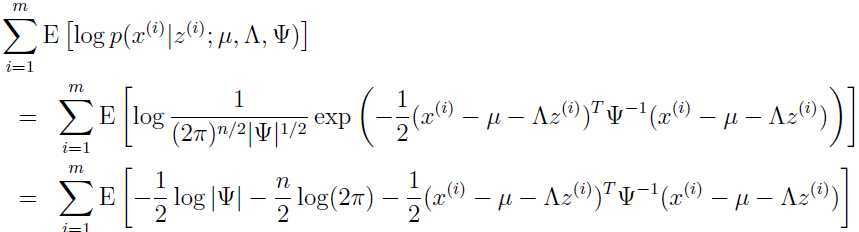
可以发现只有最后一项与参数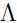 有关,利用(注意 tr 是线性代数中的“迹”):
有关,利用(注意 tr 是线性代数中的“迹”):
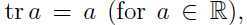
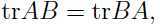
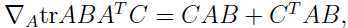
可以得到关于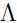 的偏导:
的偏导:
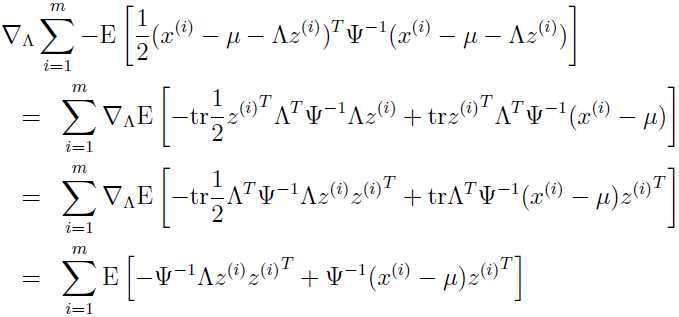
令这个偏导数为0,可以得到:
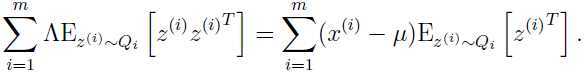
解出参数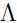 :
:
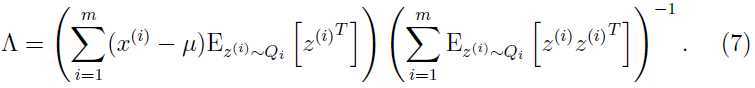
由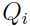 的定义知道
的定义知道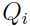 是一个均值为
是一个均值为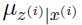 ,方差为
,方差为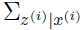 的高斯分布,很容易得到:
的高斯分布,很容易得到:
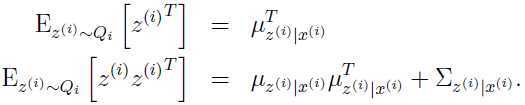
注意后面的一个等式是如何得到的:对于一个随机变量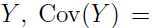
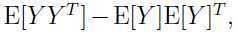 因此
因此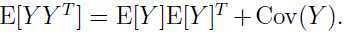
把上面连个等式的结果代入式子(7),可以得到:
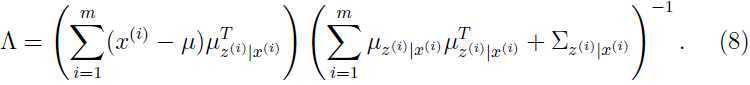
类似地,我们可以优化参数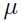 和
和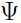 :
:
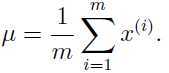
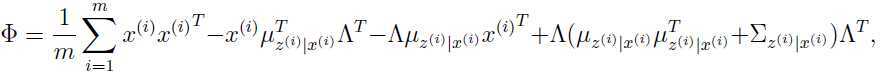
令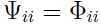 ,即
,即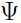 只取矩阵
只取矩阵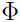 对角线上的元素.
对角线上的元素.
标签:style blog http io ar color os 使用 sp
原文地址:http://www.cnblogs.com/90zeng/p/Factor_analysis_model.html