拉格朗日乘数法

标签：style   blog   http   color   sp   strong   on   2014   问题   

拉格朗日乘数法是用来求条件极值的，极值问题有两类，其一，求函数在给定区间上的极值，对自变量

没有其它要求，这种极值称为无条件极值。其二，对自变量有一些附加的约束条件限制下的极值，称为

条件极值。例如给定椭球

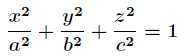
求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题，即在条件

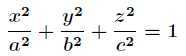
下，求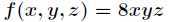的最大值。

当然这个问题实际可以先根据条件消去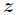，然后带入转化为无条件极值问题来处理。但是有时候这样做

很困难，甚至是做不到的，这时候就需要用拉格朗日乘数法了。如下描述

求函数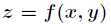在满足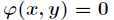下的条件极值，可以转化为函数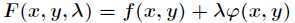

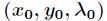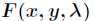的无条件极值问题。如果是函数的驻点，则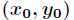就是条件极值的嫌疑点。

回到上面的题目，通过拉格朗日乘数法将问题转化为

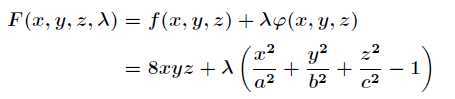
对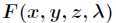求偏导得到

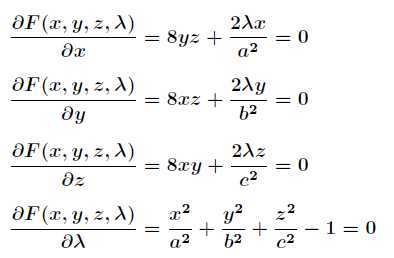
联立前面三个方程得到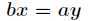和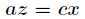，带入第四个方程解之

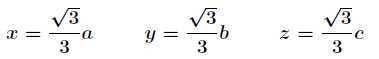
带入解得最大体积为

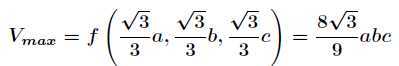
拉格朗日乘数法对一般多元函数在多个附加条件下的条件极值问题也适用。例如

题目：求旋转抛物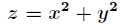面与平面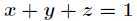的交线上到坐标原点最近的点与最远的点。

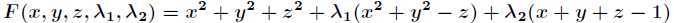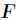分析：设，令的所有

     偏导数为零，得到

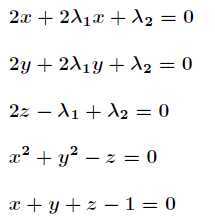
     解得两个嫌疑点分别为

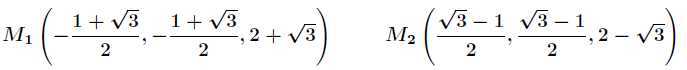
           由于

     所以，与原点最近的点是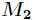，最远的点是。

拉格朗日乘数法

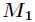标签：style   blog   http   color   sp   strong   on   2014   问题   

原文地址：http://blog.csdn.net/acdreamers/article/details/41413445