多元函数求极值问题

标签：style   blog   http   color   sp   strong   on   2014   问题   

今天来讨论多元函数求极值问题，在Logistic回归用牛顿迭代法求参数会用到，所以很有必要把它研究清楚。

回想一下，一元函数求极值问题我们是怎样做的？比如对于凹函数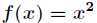，先求一阶导数，得，

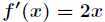由于极值处导数一定为零，但是导数等于零的点不一定就有极值，比如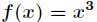。所以还需要进一步判断，对

函数继续求二阶导得到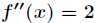，因为在驻点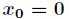处二阶导数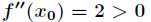成立，所以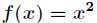

在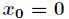处取得极小值，二阶导数在这里的意义就是判断函数局部的凹凸性。

在多元函数中求极值的方法类似，只是在判断凹凸性这里引入了一个矩阵，叫做Hessian矩阵。

如果实值多元函数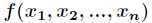在定义域内二阶连续可导，那么我们求它的极值，首先对所有求偏导，即

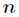得到个方程如下

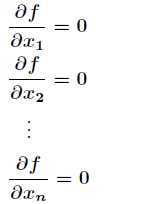
通过这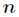个方程可以解得驻点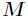，这个驻点是一个长度为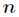的一维向量。但是我们仅仅得到这个驻点，其实在这

个驻点有3种情况，分别是：局部极大值，局部极小值和非极值。

所以接下来要做的事就是判断这个驻点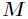属于这3个中的哪一个。所以就引入了Hessian矩阵，也就是说它用来

判断在多元函数的凹凸性问题。

Hessian矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率，常用于牛顿迭代法解决优化问题。

例如对于上面的多元函数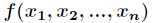，如果它的二阶偏导数都存在，那么Hessian矩阵如下

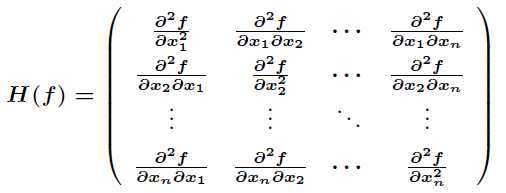
如果函数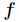在定义域内二阶连续可导，那么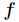的Hessian矩阵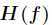在定义域内为对称矩阵，因为如果函数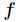连

续，则二阶偏导数的求导顺序没有区别，即

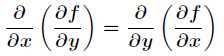
有了Hessian矩阵，我们就可以判断上述极值的3种情况了，结论如下

  （1）如果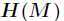是正定矩阵，则临界点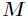处是一个局部极小值

  （2）如果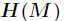是负定矩阵，则临界点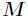处是一个局部极大值

  （3）如果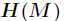是不定矩阵，则临界点处不是极值

接下来继续学习如何判断一个矩阵是否是正定的，负定的，还是不定的。

一个最常用的方法就是顺序主子式。实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零。

由于这个方法涉及到行列式的计算，比较麻烦！ 对于实二次型矩阵还有一个方法，描述如下

实二次型矩阵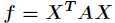为正定二次型的充要条件是的矩阵的特征值全大于零。为负定二次型的充要条

件是的矩阵的特征值全小于零，否则是不定的。

多元函数求极值问题

标签：style   blog   http   color   sp   strong   on   2014   问题   

原文地址：http://blog.csdn.net/acdreamers/article/details/41413787