Sqrt(x)

标签：style   blog   http   io   ar   color   os   sp   on   

Implement int sqrt(int x).

Compute and return the square root of x.

这里给出两种实现方法：一是二分搜索，二是牛顿迭代法。

1. 二分搜索

对于一个非负数n，它的平方根不会小于大于（n/2+1）。在[0, n/2+1]这个范围内可以进行二分搜索，求出n的平方根。

C++实现代码：

#include<iostream>
using namespace std;

class Solution {
public:
    int sqrt(int x) {
        if(x==0||x==1)
            return x;
        long long mid;
        long long left=1;
        long long right=x/2+1;
        while(left<=right)
        {
            mid=(left+right)/2;
            if(mid*mid==x)
                return mid;
            else if(mid*mid<x)
                left=mid+1;
            else
                right=mid-1;
        }
        return right;
    }
};

int main()
{
    Solution s;
    cout<<s.sqrt(2147483647)<<endl;
}

注意：要将mid声明为long long，防止mid*mid溢出。

2. 牛顿迭代法 参考：http://www.cnblogs.com/AnnieKim/archive/2013/04/18/3028607.html

   为了方便理解，就先以本题为例：

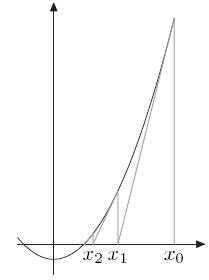
   计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

   判断x_i是否是f(x)=0的解有两种方法：

   一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f‘(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f‘(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

有了迭代公式，程序就好写了。关于牛顿迭代法，可以参考wikipedia以及百度百科。

int sqrt(int x) {
    if (x == 0) return 0;
    double last = 0;
    double res = 1;
    while (res != last)
    {
        last = res;
        res = (res + x / res) / 2;
    }
    return int(res);
}

Sqrt(x)

标签：style   blog   http   io   ar   color   os   sp   on   

原文地址：http://www.cnblogs.com/wuchanming/p/4118894.html