标签:style blog http io ar color 使用 sp for
fibonacci数列是指 0,1,1,2,3,5,8,13,21……这样自然数序列,即从第3项开始满足f(n)=f(n-1)+f(n-2);
递归实现非常简单:
long long fibonacci(unsigned int n) { int result[2] = {0, 1}; if (n < 2) return result[n]; return fibonacci(n-1) + fibonacci(n-2); }
以计算f(10)为例,必须先求得f(9)和f(8),要计算f(9),又必须先求得f(8)和f(7),如下图,可以发现存在大量重复的计算
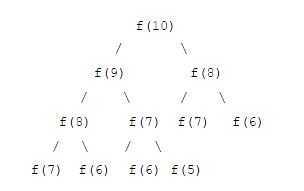
可见,当n比较大时,递归的算法效率非常低,比如计算f(100)机器就已经慢的不能接受了,用非递归的方法可以保证每个f(k)只被计算一次
long long fibonacci2(unsigned int n) { int result[2] = {0, 1}; if (n < 2) return result[n]; unsigned k; long long m = 0; long long prev = 1; long long prev_prev = 0; for (k=2; k<=n; k++) { m = prev + prev_prev; prev_prev = prev; prev = m; } return m; }
非递归的时间复杂度是O(n)。
下面介绍一种使用矩阵运算的方法,推导过程如下:
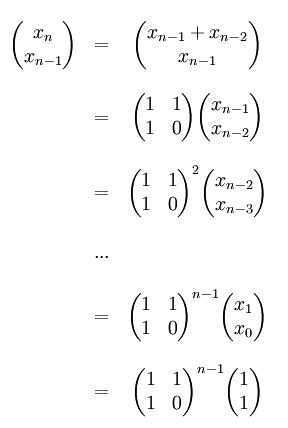
下面采用二分法计算矩阵的幂,时间复杂度只要O(logn):
void multiply(int c[2][2], int a[2][2], int b[2][2]) { int tmp[2][2]; tmp[0][0] = a[0][0]*b[0][0] + a[0][1]*b[1][0]; tmp[0][1] = a[0][0]*b[0][1] + a[0][1]*b[1][1]; tmp[1][0] = a[1][0]*b[0][0] + a[1][1]*b[1][0]; tmp[1][1] = a[1][0]*b[0][1] + a[1][1]*b[1][1]; c[0][0] = tmp[0][0]; c[0][1] = tmp[0][1]; c[1][0] = tmp[1][0]; c[1][1] = tmp[1][1]; } //二分法求矩阵幂 void matrix_pow(int a[2][2], int n) { int unit[2][2]; memcpy(unit, a, sizeof(unit)); if (n < 2) { } else if (n % 2 == 0) { multiply(a, a, a); matrix_pow(a, n/2); } else { multiply(a, a, a); matrix_pow(a, (n-1)/2); multiply(a, a, unit); } } long long fibonacci3(unsigned int n) { int result[3] = {0, 1, 1}; if (n < 3) { return result[n]; } int matrix[2][2] = {{1,1},{1,0}}; matrix_pow(matrix, n-2); return matrix[0][0] + matrix[0][1]; }
实际上,fibonacci数列有通项公式,可以直接计算第n项的值:
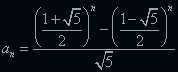
公式的具体推导过程参考这里。
在fibonacci数列中,当n趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618,例如:
1÷1=1,1÷2=0.5,2÷3=0.666...,3÷5=0.6,5÷8=0.625,…………,55÷89=0.617977…,…………144÷233=0.618025…46368÷75025=0.6180339886…...
fibonacci质数的几个结论:
推导过程可以看这里。
对一个fibonacci数列 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89……,
而一个质数序列是2, 3, 5, 7, 11, 13, 17, 19……,以这个质数序列作为项数,对应的fibonacci项为:
f(5)=5,f(7)=13,f(11)=89,这些也都是质数。
如何判断一个整数是不是在fibonacci序列中
最简单的做法是依次计算 f(1)、f(2)……、f(n),然后跟该整数比较看是否相等。
但当该整数非常大时,这种做法效率很低,一种更简单的方法参考这里,即一个数 N 如果满足 5 N^2 + 4 或 5N^2 – 4 能够开平方,则该数是fibonacci数。
一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。求总共有多少总跳法,并分析算法的时间复杂度。
首先我们考虑最简单的情况。如果只有1级台阶,那显然只有一种跳法。如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。
现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。
我们把上面的分析用一个公式总结如下:
/ 1 n=1
f(n) = 2 n=2
\ f(n-1)+(f-2) n>2
这就是我们熟悉的Fibonacci序列。
对上面的题目再改进一下:
一个台阶总共有n级,如果一次可以跳1级,也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法?
用Fib(n)表示青蛙跳上n阶台阶的跳法数,设定Fib(0) = 1,
当n = 1 时,只有一种跳法,即1阶跳:Fib(1) = 1;
当n = 2 时,有两种跳的方式,一阶跳和二阶跳:Fib(2) = Fib(1) + Fib(0) = 2;
当n = 3 时,有三种跳的方式,第一次跳出一阶后,后面还有Fib(3-1)中跳法;第一次跳出二阶后,后面还有Fib(3-2)中跳法;第一次跳出三阶后,后面还有Fib(3-3)中跳法,即Fib(3) = Fib(2) + Fib(1)+Fib(0)=4;
当n = n 时,共有n种跳的方式,第一次跳出一阶后,后面还有Fib(n-1)中跳法; 第一次跳出二阶后,后面还有Fib(n-2)中跳法..........................第一次跳出n阶后,后面还有 Fib(n-n)中跳法,得到
Fib(n) = Fib(n-1)+Fib(n-2)+Fib(n-3)+..........+Fib(n-n) = Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-1)
那么有
Fib(n-1) = Fib(0)+Fib(1)+Fib(2)+.......+Fib(n-2)
两式相减,得到 Fib(n) - Fib(n-1) = Fib(n-1),即 Fib(n) = 2*Fib(n-1)
现有长为144cm的铁丝,要截成n小段(n>2),每段的长度不小于1cm,如果其中任意三小段都不能拼成三角形,则n的最大值为多少?
由于形成三角形的充要条件是任何两边之和大于第三边,因此不构成三角形的条件就是任意两边之和不超过最大边。截成的铁丝最小为1,因此可以放2个1,第三条线段就是2(为了使得n最大,因此要使剩下来的铁丝尽可能长,因此每一条线段总是前面的相邻2段之和),依次为:1、1、2、3、5、8、13、21、34、55,以上各数之和为143,与144相差1,因此可以取最后一段为56,这时n达到最大为10。
用2X1(2行1列)的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2X1的小矩形无重复地覆盖一个2X8的大矩形,总共有多少种方法。
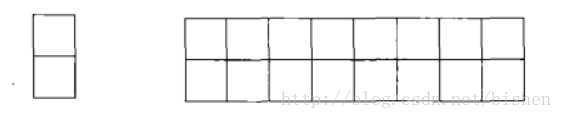
设f(8)表示覆盖2X8大矩形的方法综述。假设第一个小矩形是竖着去覆盖大矩形,那么还剩下由7个2X1的小矩形组成的大矩形f(7);假设第一个小矩形是横着去覆盖大矩形,那么还剩下由6个2X1的小矩形组成的大矩形f(6)。即f(8)=f(7)+f(6)。依此类推,最后f(1)=1,f(2)=2。使用计算斐波那契数列的方法计算这道题目即可求出答案。
参考文档:
http://blog.csdn.net/hackbuteer1/article/details/6684867
标签:style blog http io ar color 使用 sp for
原文地址:http://www.cnblogs.com/chenny7/p/4119567.html