UVa 11389 (贪心) The Bus Driver Problem

标签：style   blog   http   io   ar   color   os   sp   for   

题意：

有司机，下午路线，晚上路线各n个。给每个司机恰好分配一个下午路线和晚上路线。

给出行驶每条路线的时间，如果司机开车时间超过d，则要付加班费d×r。

问如何分配路线才能使加班费最少。

分析：

感觉上是要先排序，然后时间最长的路线配另一个时间最短的路线。

这里就严格证明一下这样贪心的正确性。

以两条路线为例，其他情况都是类似的：

不妨假设：A1≥A2，B1≤B2，水平线代表d

情况一：

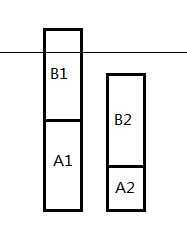
如图，司机一要付加班费，司机二不用，如果我们将B1、B2交换：

因为B1≤B2，所以付给司机一的加班费不会更少，而司机二的开车时间不会增加，所以也不用付加班费。

因此，交换以后总加班费不会减少。

情况二：

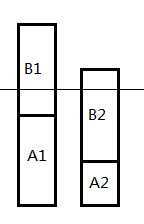
两位司机都要付加班费，则超出时间为(A1 + B1 - d) + (A2 + B2 - d)

如果交换B1、B2：

• 如果两位司机还是超出正常工作时间，那么总的加班费用不变
• 如果交换后司机一加班，司机二不加班，则超出时间为(A1 + B2 - d)。用这个减去原来的时间：(A1 + B2 - d) - (A1 + B1 - d) - (A2 + B2 - d) = d - (B1 + A2)，因为此时司机二不加班，所以原式≥0，所以总超出时间不会减少

情况三：

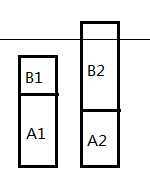
司机一不付加班费，司机二要付。此时加班时长为(A2 + B2 - d)

如果交换B1、B2：

由B1≤B2，A1≥A2，所以B2加到A1上时，司机一一定会加班，司机二一定不会加班，此时加班时长为(A1 + B2 - d)，减去原来的时间为(A1 + B2 - d) - (A2 + B2 - d) = (A1 - A2) ≥ 0

所以总加班时间不会减少。

好了，所有的情况应该都分析完了。

 1 #include <cstdio>
 2 #include <algorithm>
 3 using namespace std;
 4 
 5 const int maxn = 100 + 10;
 6 int a[maxn], b[maxn];
 7 
 8 int cmp(const int& a, const int& b)
 9 {
10     return a > b;
11 }
12 
13 int main()
14 {
15     freopen("11386in.txt", "r", stdin);
16     int n, d, r;
17     while(scanf("%d%d%d", &n, &d, &r) == 3 && n)
18     {
19         for(int i = 0; i < n; ++i) scanf("%d", &a[i]);
20         for(int i = 0; i < n; ++i) scanf("%d", &b[i]);
21         sort(a, a + n);
22         sort(b, b + n, cmp);
23         
24         int ans = 0;
25         for(int i = 0; i < n; ++i)
26             ans += max(a[i] + b[i] - d, 0) * r;
27         
28         printf("%d\n", ans);
29     }
30     
31     return 0;
32 }

代码君

UVa 11389 (贪心) The Bus Driver Problem

标签：style   blog   http   io   ar   color   os   sp   for   

原文地址：http://www.cnblogs.com/AOQNRMGYXLMV/p/4122236.html