标签:des style blog http io ar color os sp
首先构造如下一棵二元查找树(BST树):
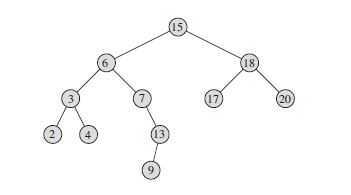
C++代码实现:
typedef struct _BSTreeNode { int value; struct _BSTreeNode *left; struct _BSTreeNode *right; } BSTreeNode; static BSTreeNode* insert(BSTreeNode* q, int x) { BSTreeNode* p = (BSTreeNode*) new(BSTreeNode); p->value = x; p->left = NULL; p->right = NULL; if (q == NULL) { q = p; } else if (x < q->value) { q->left = insert(q->left, x); } else { q->right = insert(q->right, x); } return q; } static BSTreeNode* search(BSTreeNode* p, int x) { int find = 0; while (p && !find) { if (x == p->value) { find = 1; } else if (x < p->value) { p = p->left; } else { p = p->right; } } if (p == NULL) { cout<< "not found" <<endl; } return p; } int main() { int n, key; vector<int> path; BSTreeNode *BT = NULL; int array[11] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9}; for (n=0; n<11; n++) { key = array[n]; BT = insert(BT, key); } n = 0; return 0; }
对二叉树的遍历除了常见的先序遍历/中序遍历/后序遍历意外,还有广度优先,深度优先遍历。
沿着树的宽度遍历树的结点,自上而下,从左往右的遍历一棵二叉树。
思路:考虑用队列的数据结构来实现,将根结点放入队列之后。
每次从队列头取出一个结点的同时,将其左孩子、右孩子分别放入队列尾。
void BreadthFirstSearch(BSTreeNode *root, vector<int> &result) { if (!root) return; BSTreeNode *q; deque<BSTreeNode *> queue; queue.push_back(root); while (queue.size()) { // 从队头取出一个节点 q = queue.front(); queue.pop_front(); result.push_back(q->value); if (q->left) queue.push_back(q->left); if (q->right) queue.push_back(q->right); } } int main() { int n, key; vector<int> path; BSTreeNode *p1, *p2, *p3; BSTreeNode *BT = NULL; int array[11] = {15, 6, 18, 3, 7, 17, 20, 2, 4, 13, 9}; for (n=0; n<11; n++) { key = array[n]; BT = insert(BT, key); } BreadthFirstSearch(BT, path); vector<int>::iterator it = path.begin(); for (; it!=path.end(); ++it) { cout<<*it<<"\t"; } cout<<endl; return 0; }
沿着树的深度遍历树的结点,尽可能的搜索树的分支。
思路:考虑用stack的数据结构来实现,将根结点放入stack之后。
每次从栈顶取出一个结点的同时,将其右孩子、左孩子分别压入stack。
void DepthFirstSearch(BSTreeNode* root, vector<int> &result) { if (!root) return; BSTreeNode *q; stack<BSTreeNode *> nodeStack; nodeStack.push(root); while (!nodeStack.empty()) { q = nodeStack.top(); nodeStack.pop(); result.push_back(q->value); if(q->right) nodeStack.push(q->right); if(q->left) nodeStack.push(q->left); } }
将上面的BST树转换为双向链表:如2==3==4==6==7==9==13==15==17==18==20。
我们知道,BST树的中序遍历是有序的,所以只要按这种方式将当前访问的节点加到链表末尾就可以了。
void ConvertNode(BSTreeNode *pNode, BSTreeNode** pLastNodeOfList) { if (NULL == pNode) return; if (pNode->left) { ConvertNode(pNode->left, pLastNodeOfList); } pNode->left = *pLastNodeOfList; if (*pLastNodeOfList) { (*pLastNodeOfList)->right = pNode; } *pLastNodeOfList = pNode; if (pNode->right) { ConvertNode(pNode->right, pLastNodeOfList); } } BSTreeNode* Convert_Solution(BSTreeNode* pHeadOfTree) { BSTreeNode *pLastNodeInList = NULL; ConvertNode(pHeadOfTree, &pLastNodeInList); // 找到双向链表的头指针 BSTreeNode *pHeaderOfList = pLastNodeInList; while (pHeaderOfList && pHeaderOfList->left) pHeaderOfList = pHeaderOfList->left; return pHeaderOfList; }
实现一个FindPath函数,能找到所有节点的和等于50的路径:
void FindPath(BSTreeNode* root, int sum, vector<int>&path, int ¤t) { if (!root) return; current += root->value; path.push_back(root->value); // find one path if (NULL == root->left && NULL == root->right && current == sum) { vector<int>::iterator it = path.begin(); for (; it!=path.end(); ++it) { cout<<*it<<"\t"; } cout<<endl; } if (root->left) FindPath(root->left, sum, path, current); if (root->right) FindPath(root->right, sum, path, current); current -= root->value; path.pop_back(); }
运行结果为:
[root@localhost cq]# ./a.out 15 6 7 13 9 15 18 17
实现思路:
当访问到某一节点时,将该节点添加到路径上,并累加当前节点的值:
1、如果当前节点为叶节点并且当前路径的和刚和等于输入的值,则当前路径就符合要求;
2、如果当前节点不是叶节点,则继续访问它的子节点;
3、当前节点访问结束后,递归函数将自动回到父节点。因此在函数退出之前要在路径上删除当前节点并减去当前节点的值,以确保返回父节点时路径刚好是根节点到父节点的路径。保存路径的数据结构实际上是一个栈结构,因为路径要与递归调用状态一致,而递归调用本质就是一个压栈和出栈的过程。
二叉树的后序遍历分为3部分: LETF、RIGHT、ROOT,并且,LEFT部分的值都不大于ROOT,RIGHT部分的值都大于ROOT。
因此,对一个数组,从第一个元素开始遍历,把小于最后一个元素(即ROOT)的部分作为LEFT,大于最后一个元素的部分作为RIGHT。
然后再对LEFT和RIGHT递归判断子树是否也符合条件。
C++代码实现如下:
int verifySequenceOfBST(int *seq, int N) { if (seq == NULL || N <= 0) return 0; int n, m; int root = seq[N-1]; // 根结点 for (n=0; n<N-1 && seq[n] <= root; n++); // 左子树 for (m=n; m<N-1 && seq[m] > root; m++); // 右子树 if (m != N-1) return 0; int left = 1, right = 1; if (n > 0) left = verifySequenceOfBST(seq,n); if (n < N-1) right = verifySequenceOfBST(seq+n,N-1-n); return (left && right); }
如果两个节点A、B有共同的父节点C,那么有4种情况:
1、A和B都在C的左子树中;
2、A和B都在C的右子树中;
3、A在C的左子树,B在C的右子树;
4、B在C的左子树,A在C的右子树;
我们从根节点开始,先判断属于上面哪种情况,如果是情况1,只要A、B的共同父节点肯定在左子树中,继续递归;情况2类似处理;
如果是情况3、4,那么A和B的最低共同父节点就是根节点。
C++代码实现如下:
int HasNode(BSTreeNode *pHead, BSTreeNode *pNode) { if (pHead == pNode) return 1; int has = 0; if (pHead->left) has = HasNode(pHead->left, pNode); if (!has && pHead->right) has = HasNode(pHead->right, pNode); return has; } BSTreeNode *LastCommonParent(BSTreeNode *pHead, BSTreeNode *pNode1, BSTreeNode *pNode2) { if (NULL == pHead || NULL == pNode1 || NULL == pNode2) return NULL; int leftHasNode1 = 0; int leftHasNode2 = 0; if (pHead->left) { leftHasNode1 = HasNode(pHead->left, pNode1); leftHasNode2 = HasNode(pHead->left, pNode2); } if (leftHasNode1 && leftHasNode2) { // 两个结点都在左子树中 if (pHead->left == pNode1 || pHead->left == pNode2) return pHead; return LastCommonParent(pHead->left, pNode1, pNode2); } int rightHasNode1 = 0; int rightHasNode2 = 0; if (pHead->right) { if (!leftHasNode1) rightHasNode1 = HasNode(pHead->right, pNode1); if (!leftHasNode2) rightHasNode2 = HasNode(pHead->right, pNode2); } if (rightHasNode1 && rightHasNode2) { // 两个结点都在右子树中 if (pHead->right == pNode1 || pHead->right == pNode2) return pHead; return LastCommonParent(pHead->right, pNode1, pNode2); } if ((leftHasNode1 && rightHasNode2) // 两个结点一个在左子树中,另一个在右子树中 || (leftHasNode2 && rightHasNode1)) return pHead; return NULL; }
思路:要在树A中查找是否存在和树B结构一样的子树,可以分为两步:
1、在树A中找到和B的根节点一样的节点N;
2、判断树A中以N为根节点的子树是不是包括和树B一样的结构。
递归的实现方式如下:
int TreeEqual(BSTreeNode* Head1, BSTreeNode* Head2) { if (NULL == Head2) return 1; if (NULL == Head1) return 0; if (Head1->value != Head2->value) return 0; return TreeEqual(Head1->left, Head2->left) && TreeEqual(Head1->right, Head2->right); } int HasSubTreeCore(BSTreeNode* Head1, BSTreeNode* Head2) { int result = 0; if (Head1->value == Head2->value) { result = TreeEqual(Head1, Head2); } if (result == 0 && Head1->left) { result = TreeEqual(Head1->left, Head2); } if (result == 0 && Head1->right) { result = TreeEqual(Head1->right, Head2); } return result; } int HasSubTree(BSTreeNode* Head1, BSTreeNode* Head2) { if ((Head1 == NULL && Head2 != NULL) || (Head1 != NULL && Head2 == NULL)) return 0; if (Head1 == NULL && Head2 == NULL) return 1; return HasSubTreeCore(Head1, Head2); }
标签:des style blog http io ar color os sp
原文地址:http://www.cnblogs.com/chenny7/p/4120961.html