标签:style blog http io ar color os 使用 sp
作者:jostree 转载请注明出处 http://www.cnblogs.com/jostree/p/4098136.html
给定一个非负整数序列$D=\{d_1,d_2,...d_n\}$,若存在一个无向图使得图中各点的度与此序列一一对应,则称此序列可图化。进一步,若图为简单图,则称此序列可简单图化。
可图化的判定为:$d_1+d_2+ \cdots +d_n=0(mod2)$。即把奇数度的点配对,剩下的变为自环。
可简单图化的判定,即Havel-Hakimi定理:
我们把序列$D$变换为非增序列,即$d_1\geq d_2\geq \cdots \geq d_n$,则$D$可简单图化当且仅当$D‘=(d_2-1, d_3-1, \cdots ,d_{(d1+1)}-1, d_{d1+2}, d_{d1+3}, \cdots ,d_n)$可简单图化。
证明:
<--:若$D‘$可简单图化,把原图$G_D$中的最大度点与$G_{D‘}$中度最大的$d_1$个点连边即可,图$G_D$必为简单图。
-->:若$D$可简单图化,设得到的简单图为$D_G$。分两种情况考虑:
(a)若$G_D$中存在边$(v_1,v_2), (v_1,v_3), \dots ,(v_1,v_{d_1+1})$,则删除这些边得简单图$G_{D‘}$,于是$D‘$可简单图化为$G_{D‘}$
(b)若存在点$v_i,v_j(i<j)$且$(v_1,v_i)$不在$G_D$中,但$(v_1,v_j)$在$G_D$中。这时,因为$d_i \geq d_j$,必存在$k$使得$(v_i, v_k)$在$D_G$中但$(v_j,v_k)$不在$G_D$中。这时我们可以令$G‘‘=G_D-\{(v_i,v_k),(v_1,v_j)\}+\{(v_k,v_j),(v_1,v_i)\}$。$G‘‘$的度序列仍为$D$,使用情况(a)处理。
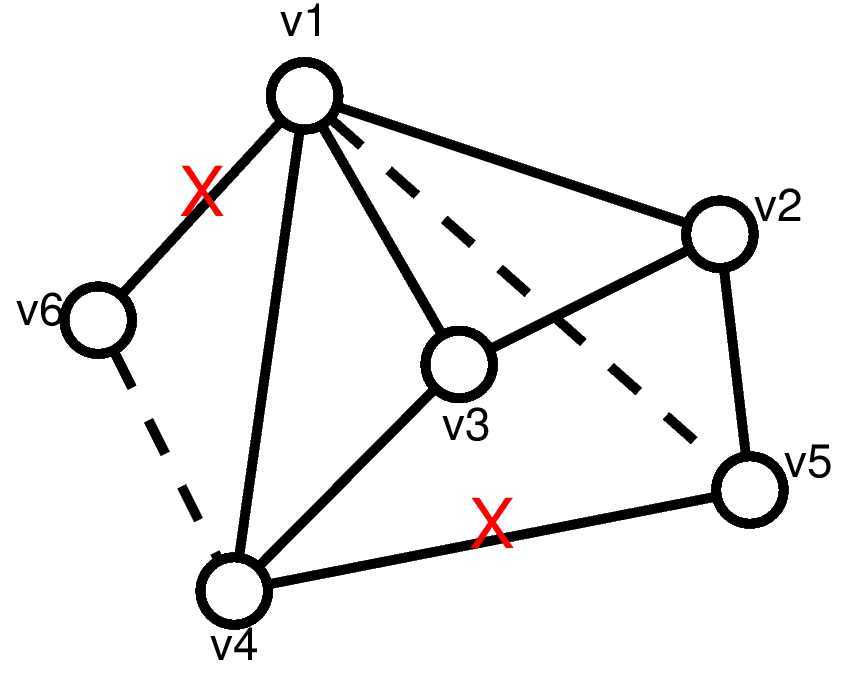
例如对于下图,我们删除两条打红X的边,添加两条虚线的边,即可转化为$G‘‘$
代码实现很简单,每次对数组arr排序,然后对于arr[1],arr[2],...,arr[arr[0]]每个数减一,并另arr[0]=0。重复n次,最后检验数组是否全部为0,是则输出YES和图,否则输出NO。
需要注意的是输出格式,每两个case之间需要输出一个空行。
代码如下:

1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <cstring> 5 #include <algorithm> 6 #define MAXN 11 7 using namespace std; 8 class node 9 { 10 public: 11 int id; 12 int degree; 13 bool operator < (const node & a)const 14 { 15 return degree>a.degree; 16 } 17 }; 18 int n; 19 node arr[MAXN]; 20 int map[MAXN][MAXN]; 21 void solve() 22 { 23 memset(map, 0, sizeof(map)); 24 for( int i = 0 ; i < n ; i++ ) 25 { 26 sort(arr, arr+n); 27 for( int j = 1 ; j <= arr[0].degree ; j++ ) 28 { 29 arr[j].degree -= 1; 30 map[arr[0].id][arr[j].id] = 1; 31 map[arr[j].id][arr[0].id] = 1; 32 } 33 arr[0].degree = 0; 34 } 35 for( int i = 0 ; i < n ; i++ ) 36 { 37 if( arr[i].degree < 0 ) 38 { 39 printf("NO\n\n"); 40 return ; 41 } 42 } 43 printf("YES\n"); 44 for( int i = 0 ; i < n ; i++ ) 45 { 46 for( int j = 0 ; j < n ; j++ ) 47 { 48 printf("%d%c", map[i][j], j==(n-1)?‘\n‘:‘ ‘); 49 } 50 } 51 printf("\n"); 52 } 53 int main(int argc, char *argv[]) 54 { 55 int t; 56 scanf("%d", &t); 57 while( t-- ) 58 { 59 scanf("%d", &n); 60 for( int i = 0 ; i < n ; i++ ) 61 { 62 scanf("%d", &arr[i].degree); 63 arr[i].id = i; 64 } 65 solve(); 66 } 67 }
poj 1659 Frogs' Neighborhood Havel-Hakimi定理 可简单图定理
标签:style blog http io ar color os 使用 sp
原文地址:http://www.cnblogs.com/jostree/p/4098136.html