标签:style blog http io ar color os sp div
数的构造同插入函数那篇文章的构造。
主要增加了查找父节点和删除的函数,同时为了方便删除了插入的函数。
获取父节点的函数如下:
1 BTree *getFather(BTree *root,BTree *child) 2 { 3 if (root == child) 4 return nullptr; 5 if (root->left == child || root->right == child) 6 return root; 7 if (root->data > child->data) 8 return getFather(root->left, child); 9 else 10 return getFather(root->right, child); 11 }
删除的函数如下:
1 void deleteNode(BTree *&root,int data) 2 { 3 BTree *father = nullptr; 4 BTree *cur = nullptr; 5 BTree *newRoot = nullptr; 6 BTree *tmp = nullptr; 7 cur = findKey(root, data);//查找到要进行删除的节点 8 if (cur == nullptr) 9 { 10 log("没有此节点"); 11 return ; 12 } 13 father = getFather(root, cur); 14 if (father == nullptr) 15 { 16 log("没有父节点");//那么他是根节点 17 newRoot=findMin(root->right);//将其右子树的最小值提取出来当作根节点 18 father = getFather(root,newRoot);//获取新根原来的父节点 19 father->left = nullptr;//新根一定是从其父节点左侧取出的 20 newRoot->left=root->left; 21 newRoot->right = root->right; 22 free(root); 23 root = newRoot; 24 return; 25 } 26 if (father->left == cur)//获取到了要被删除节点的父亲,若在其父亲的左侧 27 { 28 if (cur->left == nullptr && cur->right != nullptr) 29 { 30 father->left = cur->right; 31 free(cur); 32 return; 33 } 34 else if (cur->right == nullptr && cur->left != nullptr) 35 { 36 father->left = cur->left; 37 free(cur); 38 return; 39 } 40 else if (cur->left == nullptr&& cur->right == nullptr) 41 { 42 free(cur); 43 father->left = nullptr; 44 return; 45 } 46 else 47 { 48 father->left = findMin(cur->right);//将右子树中的最小值替代被删除的节点 49 50 tmp = getFather(cur, father->left);//找到替代节点的父亲 51 tmp->left = nullptr; 52 53 father->left->left = cur->left; 54 father->left->right = cur->right; 55 free(cur); 56 return; 57 } 58 } 59 else if (father->right == cur)//若在其父亲的右侧 60 { 61 62 if (cur->left == nullptr && cur->right != nullptr) 63 { 64 father->right = cur->right; 65 free(cur); 66 return; 67 } 68 else if (cur->right == nullptr && cur->left != nullptr) 69 { 70 father->right = cur->left; 71 free(cur); 72 return; 73 } 74 else if (cur->left == nullptr && cur->right == nullptr) 75 { 76 free(cur); 77 father->right = nullptr; 78 return; 79 } 80 else 81 { 82 father->right = findMin(cur->right);//将右子树中的最小值替代被删除的节点 83 84 tmp = getFather(cur, father->right);//找到替代节点的父亲 85 tmp->left = nullptr; 86 87 father->right->left = cur->left; 88 father->right->right = cur->right; 89 free(cur); 90 return; 91 } 92 } 93 94 }
全部源代码如下:
SearchTree.cpp
1 #include "iostream" 2 #include "stdlib.h" 3 4 #define log(s); std::cout<<s<<std::endl; 5 6 typedef struct _btree_ 7 { 8 int data; 9 struct _btree_ *left; 10 struct _btree_ *right; 11 }BTree; 12 13 BTree *createNode(int data) 14 { 15 BTree *p = (BTree *)malloc(sizeof(BTree)); 16 p->data = data; 17 p->left = nullptr; 18 p->right = nullptr; 19 return p; 20 } 21 22 BTree *findKey(BTree *father,int data) 23 { 24 if (father == nullptr) 25 return nullptr; 26 if (father->data < data) 27 return findKey(father->right, data); 28 else if (father->data > data) 29 return findKey(father->left, data); 30 else if (father->data == data) 31 return father; 32 } 33 34 BTree *findMax(BTree *root) 35 { 36 if (root != nullptr) 37 while (root->right != nullptr) 38 root = root->right; 39 return root; 40 } 41 42 BTree *findMin(BTree *root) 43 { 44 if (root->left == nullptr) 45 return root; 46 else 47 return findMin(root->left); 48 } 49 50 BTree *createTree(BTree *&root) 51 { 52 BTree *t1, *t2, *t4, *t3, *t6, *t7, *t8, *t9, *t10; 53 t1 = createNode(1); 54 t2 = createNode(9); 55 t3 = createNode(7); 56 t4 = createNode(5); 57 t6 = createNode(15); 58 t7 = createNode(11); 59 t8 = createNode(19); 60 t9 = createNode(17); 61 t10 = createNode(20); 62 root->left = t4; 63 root->right = t6; 64 t4->left = t1; 65 t4->right = t2; 66 t2->left = t3; 67 t6->left = t7; 68 t6->right = t8; 69 t8->left = t9; 70 t8->right = t10; 71 return root; 72 } 73 74 BTree *getFather(BTree *root,BTree *child) 75 { 76 if (root == child) 77 return nullptr; 78 if (root->left == child || root->right == child) 79 return root; 80 if (root->data > child->data) 81 return getFather(root->left, child); 82 else 83 return getFather(root->right, child); 84 } 85 86 void deleteNode(BTree *&root,int data) 87 { 88 BTree *father = nullptr; 89 BTree *cur = nullptr; 90 BTree *newRoot = nullptr; 91 BTree *tmp = nullptr; 92 cur = findKey(root, data);//查找到要进行删除的节点 93 if (cur == nullptr) 94 { 95 log("没有此节点"); 96 return ; 97 } 98 father = getFather(root, cur); 99 if (father == nullptr) 100 { 101 log("没有父节点");//那么他是根节点 102 newRoot=findMin(root->right);//将其右子树的最小值提取出来当作根节点 103 father = getFather(root,newRoot);//获取新根原来的父节点 104 father->left = nullptr;//新根一定是从其父节点左侧取出的 105 newRoot->left=root->left; 106 newRoot->right = root->right; 107 free(root); 108 root = newRoot; 109 return; 110 } 111 if (father->left == cur)//获取到了要被删除节点的父亲,若在其父亲的左侧 112 { 113 if (cur->left == nullptr && cur->right != nullptr) 114 { 115 father->left = cur->right; 116 free(cur); 117 return; 118 } 119 else if (cur->right == nullptr && cur->left != nullptr) 120 { 121 father->left = cur->left; 122 free(cur); 123 return; 124 } 125 else if (cur->left == nullptr&& cur->right == nullptr) 126 { 127 free(cur); 128 father->left = nullptr; 129 return; 130 } 131 else 132 { 133 father->left = findMin(cur->right);//将右子树中的最小值替代被删除的节点 134 135 tmp = getFather(cur, father->left);//找到替代节点的父亲 136 tmp->left = nullptr; 137 138 father->left->left = cur->left; 139 father->left->right = cur->right; 140 free(cur); 141 return; 142 } 143 } 144 else if (father->right == cur)//若在其父亲的右侧 145 { 146 147 if (cur->left == nullptr && cur->right != nullptr) 148 { 149 father->right = cur->right; 150 free(cur); 151 return; 152 } 153 else if (cur->right == nullptr && cur->left != nullptr) 154 { 155 father->right = cur->left; 156 free(cur); 157 return; 158 } 159 else if (cur->left == nullptr && cur->right == nullptr) 160 { 161 free(cur); 162 father->right = nullptr; 163 return; 164 } 165 else 166 { 167 father->right = findMin(cur->right);//将右子树中的最小值替代被删除的节点 168 169 tmp = getFather(cur, father->right);//找到替代节点的父亲 170 tmp->left = nullptr; 171 172 father->right->left = cur->left; 173 father->right->right = cur->right; 174 free(cur); 175 return; 176 } 177 } 178 179 } 180 181 int main(void) 182 { 183 BTree *root = nullptr; 184 root = createNode(10); 185 root = createTree(root); 186 deleteNode(root, 15); 187 system("pause"); 188 return 0; 189 }
树的结构再次贴一下:
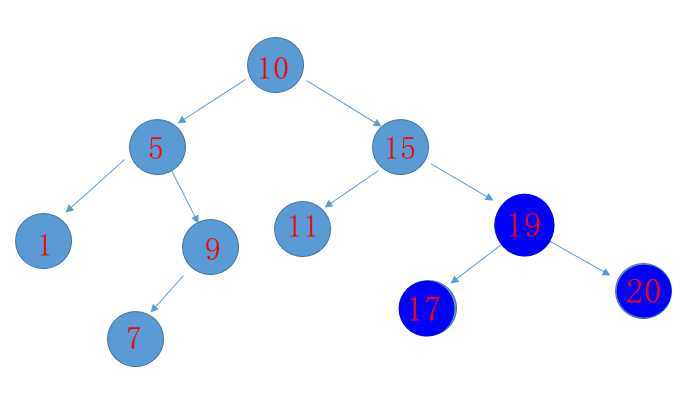
深色的是原本的树有误更改之后的。
代码未经严格测试,如有错误,希望读者指出,不胜感激。
以上。
标签:style blog http io ar color os sp div
原文地址:http://www.cnblogs.com/lhyz/p/4127485.html