标签:des blog http io ar 使用 sp java on
转载:http://blog.renren.com/share/119427502/14133720846
最近在摆弄数据离散度的时候遇到一种图形,叫做盒图(boxplot)。它对于显示数据的离散的分布情况效果不错。
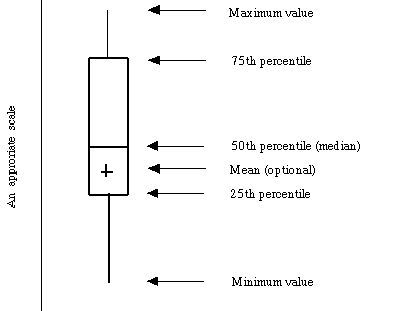
盒图是在1977年由美国的统计学家约翰·图基(John Tukey)发明的。它由五个数值点组成:最小值(min),下四分位数(Q1),中位数(median),上四分位数(Q3),最大值(max)。也可以往盒图里面加入平均值(mean)。如上图。下四分位数、中位数、上四分位数组成一个“带有隔间的盒子”。上四分位数到最大值之间建立一条延伸线,这个延伸线成为“胡须(whisker)”。
由于现实数据中总是存在各式各样地“脏数据”,也成为“离群点”,于是为了不因这些少数的离群数据导致整体特征的偏移,将这些离群点单独汇出,而盒图中的胡须的两级修改成最小观测值与最大观测值。这里有个经验,就是最大(最小)观测值设置为与四分位数值间距离为1.5个IQR(中间四分位数极差)。即
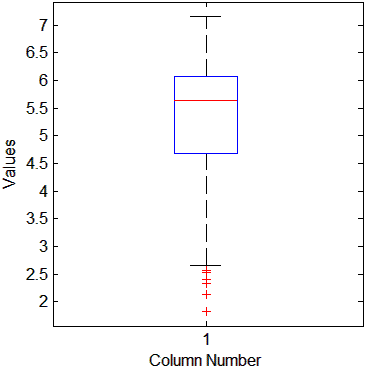
通过盒图,在分析数据的时候,盒图能够有效地帮助我们识别数据的特征:
1.箱体的左侧(下)边界代表第一四分位(Q1),而右侧(上)边界代表第三四分位(Q3)。至于箱体部分代表四分位距(IQR),也就是观测值的中间50%值。
2.在箱体中间的线代表的是数据的中位数值。
3.从箱体边缘延伸出去的直线称为触须(whisker).触须(whisker)的向外延伸表示了数据集中的最大和最小(异常点除外)。
4.极端值或异常点(outlier),用星号(*)来标识.如果一个值位于箱体外面(大于Q3或小于Q1),并且距离相应边界大于1.5倍的IQR,那么这个点就被认为是一个异常点(outlier)。
如果你选择通过分组变量(By variable)来分组数据,MINITAB将把图像变成垂直放置,否则图形将水平放置。
使用箱形图来评估数据的对称性:
1.如果数据是明显对称,中位数值线将近似位于四分位距箱体的中间,上下触须(whisker)在长度上将近似相等。
2.如果数据是偏态的,中位数将可能不位于四分位距(IQR)箱体的中间,某一触须(whisker)将可能显著地比另一个长。
在降水数据的箱形图(boxplot)中,中位数位于四分位距(IQR)箱体的中间,上下触须(whisker)长度相等.这表明除了异常点(outlier)星号(*)外,数据是对成的.这很好的说明了异常点(outlier)可能和其它的样本数据不是来自同一个母体(population)。
我们结合Minitab帮助就会知道,
假定有数据列C1:1 2 3 4 5 6 7 8,C2:1 2 3 4 5 6 7 8 9,
对于Median(中位数)的位置,这个值等于(N+1)/2,比如C1,共有8个数据,那么中位数就等于(4+5)/2=4.5.由于结果并不是整数,也就是说中位数位于第4和5数数(我们把它们记为X(4)和X(5))之间,那么中位数等于=X(4)+0.5(X(5)-X(4))=4+0.5(5-4)=4.5.
对于Q1(第一四分位)的位置,这个值等于(N+1)/4,这里N表示数据个数,对于C1来说就是(8+1)/4=2.25,由于结果不是整数,也就是说Q1位于第2和3个数(我们把它们记为X(2)和X(3))之间,那么Q1=X(2)+0.25(X(3)-X(2))=2+0.25(3-2)=2.25.
对于Q3(第三四分位)的位置,这个值等于3(N+1)/4,这里N表示数据个数,对于C1来说就是3(8+1)/4=6.75,也就是说Q3位于第6和7个数(我们把它们记为X(6)和X(7))之间,
那么Q3=X(6)+0.75(X(7)-X(6))=6+0.75(7-6)=6.75.
我们可以通过在MINITAB中计算来验证结果
我们新建一个工作表,在C1列输入1 2 3 4 5 6 7 8
在C2列输入1 2 3 4 5 6 7 8 9,
我们通过菜单Stat>Basic Statistics>Display Descriptive Statistics,在Variables处输入c1 c2,然后点击Statistics按钮,只选中First quartile,Median和Third quartile统计指标,点击OK.就会在对话(session)窗口看到结果.
| Variable | Q1 | Median | Q3 |
| C1 | 2.250 | 4.500 | 6.750 |
| C2 | 2.500 | 5.000 | 7.500 |
使用箱形图(也称为箱体-触须图)来评估和比较样本分布。下面的图形图解了箱形图默认的组成部分。
异常点(Outlier)-某个异常大或小的观测点。任何超过触须的值就是异常点。
默认情况下,箱体的顶端是第三四分位(Q3)-75%的数据值小于或等于这个值。
默认情况下,箱体的底部是第一四分位(Q1)-25%的数据值小于或等于这个值。
默认情况下,下部的触须会伸展到最小值,但一定位于下限范围内。
下限(Lower limit)=Q1-1.5(Q3-Q1)
中位数-数据的中间点。一半的观测值小于或等于它。
默认情况下,上部的触须会伸展到最大值,但一定位于上限范围内。
上限(Upper limit)=Q3+1.5(Q3-Q1)
标签:des blog http io ar 使用 sp java on
原文地址:http://www.cnblogs.com/zhanglianbo/p/4128081.html