标签:style blog http io ar color os sp for
邻接矩阵有向图是指通过邻接矩阵表示的有向图。
上面的图G2包含了"A,B,C,D,E,F,G"共7个顶点,而且包含了"<A,B>,<B,C>,<B,E>,<B,F>,<C,E>,<D,C>,<E,B>,<E,D>,<F,G>"共9条边。
上图右边的矩阵是G2在内存中的邻接矩阵示意图。A[i][j]=1表示第i个顶点到第j个顶点是一条边,A[i][j]=0则表示不是一条边;而A[i][j]表示的是第i行第j列的值;例如,A[1,2]=1,表示第1个顶点(即顶点B)到第2个顶点(C)是一条边。
1. 基本定义
// 邻接矩阵 typedef struct _graph { char vexs[MAX]; // 顶点集合 int vexnum; // 顶点数 int edgnum; // 边数 int matrix[MAX][MAX]; // 邻接矩阵 }Graph, *PGraph;
Graph是邻接矩阵对应的结构体。
vexs用于保存顶点,vexnum是顶点数,edgnum是边数;matrix则是用于保存矩阵信息的二维数组。例如,matrix[i][j]=1,则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点;matrix[i][j]=0,则表示它们不是邻接点。
2. 创建矩阵
C实现代码:
#include<stdio.h> #include<stdlib.h> #include<string.h> #include<malloc.h> #define MAX 100 typedef struct graph { char vexs[MAX]; int vexnum; int edgnum; int matrix[MAX][MAX]; } Graph,*graph; static int get_position(Graph g,char ch) { int i; for(i=0;i<g.vexnum;i++) if(g.vexs[i]==ch) return i; return -1; } graph create_graph() { char vexs[]= {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘}; char edges[][2]= {{‘A‘,‘C‘},{‘A‘,‘D‘},{‘A‘,‘F‘},{‘B‘,‘C‘},{‘C‘,‘D‘},{‘E‘,‘G‘},{‘F‘,‘G‘}}; int vlen=sizeof(vexs)/sizeof(vexs[0]); int elen=sizeof(edges)/sizeof(edges[0]); int i,p1,p2; Graph *pG; if((pG=(graph)malloc(sizeof(Graph)))==NULL) return NULL; pG->edgnum=elen; pG->vexnum=vlen; for(i=0;i<pG->vexnum;i++) pG->vexs[i]=vexs[i]; for(i=0;i<pG->edgnum;i++) { p1=get_position(*pG,edges[i][0]); p2=get_position(*pG,edges[i][1]); pG->matrix[p1][p2]=1; } return pG; } void print_graph(Graph G) { int i,j; for(i=0;i<G.vexnum;i++) { for(j=0;j<G.edgnum;j++) { printf("%d ",G.matrix[i][j]); } printf("\n"); } printf("\n"); } int main() { Graph *pG; pG=create_graph(); print_graph(*pG); }
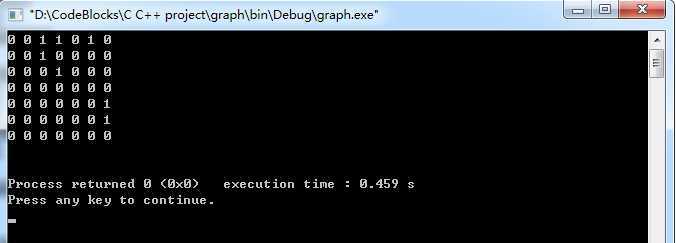
运行结果:
标签:style blog http io ar color os sp for
原文地址:http://www.cnblogs.com/wuchanming/p/4146032.html