标签:style blog http io ar color os sp for
1. 深度优先搜索介绍
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
显然,深度优先搜索是一个递归的过程。
2. 深度优先搜索图解
2.1 无向图的深度优先搜索
下面以"无向图"为例,来对深度优先搜索进行演示。
对上面的图G1进行深度优先遍历,从顶点A开始。
第1步:访问A。
第2步:访问(A的邻接点)C。
在第1步访问A之后,接下来应该访问的是A的邻接点,即"C,D,F"中的一个。但在本文的实现中,顶点ABCDEFG是按照顺序存储,C在"D和F"的前面,因此,先访问C。
第3步:访问(C的邻接点)B。
在第2步访问C之后,接下来应该访问C的邻接点,即"B和D"中一个(A已经被访问过,就不算在内)。而由于B在D之前,先访问B。
第4步:访问(C的邻接点)D。
在第3步访问了C的邻接点B之后,B没有未被访问的邻接点;因此,返回到访问C的另一个邻接点D。
第5步:访问(A的邻接点)F。
前面已经访问了A,并且访问完了"A的邻接点B的所有邻接点(包括递归的邻接点在内)";因此,此时返回到访问A的另一个邻接点F。
第6步:访问(F的邻接点)G。
第7步:访问(G的邻接点)E。
因此访问顺序是:A -> C -> B -> D -> F -> G -> E
2.2 有向图的深度优先搜索
下面以"有向图"为例,来对深度优先搜索进行演示。
对上面的图G2进行深度优先遍历,从顶点A开始。
第1步:访问A。
第2步:访问B。
在访问了A之后,接下来应该访问的是A的出边的另一个顶点,即顶点B。
第3步:访问C。
在访问了B之后,接下来应该访问的是B的出边的另一个顶点,即顶点C,E,F。在本文实现的图中,顶点ABCDEFG按照顺序存储,因此先访问C。
第4步:访问E。
接下来访问C的出边的另一个顶点,即顶点E。
第5步:访问D。
接下来访问E的出边的另一个顶点,即顶点B,D。顶点B已经被访问过,因此访问顶点D。
第6步:访问F。
接下应该回溯"访问A的出边的另一个顶点F"。
第7步:访问G。
因此访问顺序是:A -> B -> C -> E -> D -> F -> G
无向图的邻接矩阵实现代码:
#include<stdio.h> #include<stdlib.h> #include<malloc.h> #include<string.h> #define MAX 100 typedef struct graph { char vexs[MAX]; int vexnum; int edgnum; int matrix[MAX][MAX]; }Graph,*PGraph; static int get_position(Graph g,char ch) { int i; for(i=0;i<g.vexnum;i++) if(g.vexs[i]==ch) return i; return -1; } Graph* create_graph() { char vexs[]={‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘}; char edges[][2]={{‘A‘,‘C‘},{‘A‘,‘D‘},{‘A‘,‘F‘},{‘B‘,‘C‘},{‘C‘,‘D‘},{‘E‘,‘G‘},{‘F‘,‘G‘}}; int vlen=sizeof(vexs)/sizeof(vexs[0]); int elen=sizeof(edges)/sizeof(edges[0]); int i,p1,p2; Graph *pG; if((pG=(Graph*)malloc(sizeof(Graph)))==NULL) return NULL; memset(pG,0,sizeof(Graph)); pG->vexnum=vlen; pG->edgnum=elen; for(i=0;i<pG->vexnum;i++) { pG->vexs[i]=vexs[i]; } for(i=0;i<pG->edgnum;i++) { p1=get_position(*pG,edges[i][0]); p2=get_position(*pG,edges[i][1]); pG->matrix[p1][p2]=1; pG->matrix[p2][p1]=1; } return pG; } void print_graph(Graph G) { int i,j; printf("matrix Graph:\n"); for(i=0;i<G.vexnum;i++) { for(j=0;j<G.vexnum;j++) printf("%d ",G.matrix[i][j]); printf("\n"); } } int first_vertex(Graph G,int v) { int i; for(i=0;i<G.vexnum;i++) if(G.matrix[v][i]==1) return i; return -1; } int next_vertex(Graph G,int v,int w) { int i; for(i=w+1;i<G.vexnum;i++) if(G.matrix[v][i]==1) return i; return -1; } void DFS(Graph G,int i,int *visited) { visited[i]=1; int w; printf("%c ",G.vexs[i]); for(w=first_vertex(G,i);w>=0;w=next_vertex(G,i,w)) { if(visited[w]==0) DFS(G,w,visited); } } void DFSTraverse(Graph G) { int i; int visited[MAX]; memset(visited,0,sizeof(visited)); printf("DFS : \n"); for(i=0;i<G.vexnum;i++) if(!visited[i]) DFS(G,i,visited); printf("\n"); } int main() { Graph *pG; pG=create_graph(); print_graph(*pG); printf("\n"); DFSTraverse(*pG); }
运行结果:
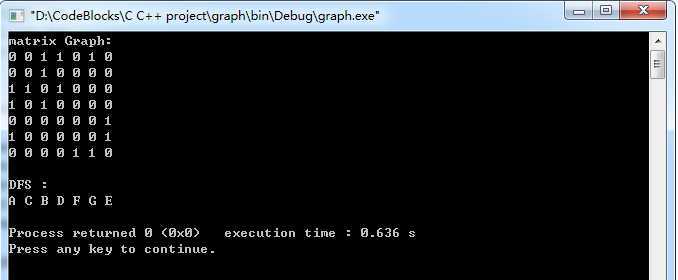
无向图的邻接表实现代码:
#include<stdio.h> #include<stdlib.h> #include<string.h> #include<malloc.h> #define MAX 100 typedef struct ENode { int ivex; struct ENode *next_edge; }ENode; typedef struct VNode { char data; ENode *first_edge; }VNode; typedef struct LGraph { int vexnum; int edgnum; VNode vexs[MAX]; } LGraph; static int get_position(LGraph g,char ch) { int i; for(i=0;i<g.vexnum;i++) if(g.vexs[i].data==ch) return i; return -1; } LGraph* create_lgraph() { char c1,c2; char vexs[]= {‘A‘,‘B‘,‘C‘,‘D‘,‘E‘,‘F‘,‘G‘}; char edges[][2]= {{‘A‘,‘C‘},{‘A‘,‘D‘},{‘A‘,‘F‘},{‘B‘,‘C‘},{‘C‘,‘D‘},{‘E‘,‘G‘},{‘F‘,‘G‘}}; int vlen=sizeof(vexs)/sizeof(vexs[0]); int elen=sizeof(edges)/sizeof(edges[0]); int i,p1,p2; ENode *node1,*node2; LGraph *pG; if((pG=(LGraph*)malloc(sizeof(LGraph)))==NULL) return NULL; memset(pG,0,sizeof(LGraph)); pG->vexnum=vlen; pG->edgnum=elen; for(i=0;i<pG->vexnum;i++) { pG->vexs[i].data=vexs[i]; pG->vexs[i].first_edge=NULL; } for(i=0;i<pG->edgnum;i++) { c1=edges[i][0]; c2=edges[i][1]; p1=get_position(*pG,c1); p2=get_position(*pG,c2); node1=(ENode*)malloc(sizeof(ENode)); node1->ivex=p2; node1->next_edge=NULL; if(pG->vexs[p1].first_edge==NULL) pG->vexs[p1].first_edge=node1; else { ENode *tmp=pG->vexs[p1].first_edge; while(tmp->next_edge) { tmp=tmp->next_edge; } tmp->next_edge=node1; } node2=(ENode*)malloc(sizeof(ENode)); node2->ivex=p1; node2->next_edge=NULL; if(pG->vexs[p2].first_edge==NULL) pG->vexs[p2].first_edge=node2; else { ENode *tmp=pG->vexs[p2].first_edge; while(tmp->next_edge) { tmp=tmp->next_edge; } tmp->next_edge=node2; } } return pG; } void print_lgraph(LGraph G) { int i; ENode *node; printf("list Graph:\n"); for(i=0;i<G.vexnum;i++) { printf("%d(%c): ",i,G.vexs[i].data); node=G.vexs[i].first_edge; while(node) { printf("%d(%c) ",node->ivex,G.vexs[node->ivex].data); node=node->next_edge; } printf("\n"); } printf("\n"); } int main() { LGraph *pG; pG=create_lgraph(); print_lgraph(*pG); }
运行结果:
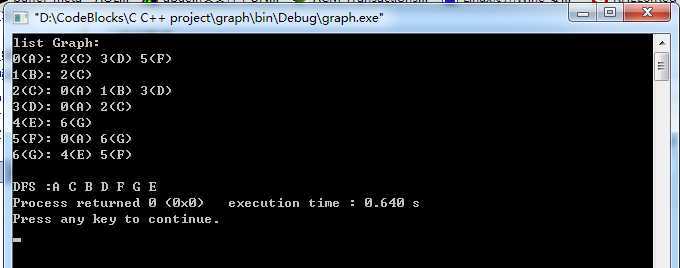
有向图与无向图的DFS一样,只是创建图的方式不一样。
标签:style blog http io ar color os sp for
原文地址:http://www.cnblogs.com/wuchanming/p/4146241.html