POJ 1577 Falling Leaves 二叉树操作

 
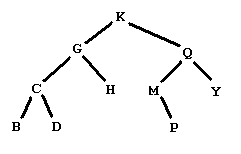
Figure 1
Figure 1 shows a graphical representation of a binary tree of letters. People familiar with binary trees can skip over the definitions of a binary tree of letters, leaves of a binary tree, and a binary search tree of letters, and go right to The problem. 

A binary tree of letters may be one of two things: 

1. It may be empty. 
   
2. It may have a root node. A node has a letter as data and refers to a left and a right subtree. The left and right subtrees are also binary trees of letters.

In the graphical representation of a binary tree of letters: 

1. Empty trees are omitted completely. 
   
2. Each node is indicated by 
   
   • Its letter data, 
     
   • A line segment down to the left to the left subtree, if the left subtree is nonempty, 
     
   • A line segment down to the right to the right subtree, if the right subtree is nonempty.

A leaf in a binary tree is a node whose subtrees are both empty. In the example in Figure 1, this would be the five nodes with data B, D, H, P, and Y. 

The preorder traversal of a tree of letters satisfies the defining properties: 

1. If the tree is empty, then the preorder traversal is empty. 
   
2. If the tree is not empty, then the preorder traversal consists of the following, in order 
   
   • The data from the root node, 
     
   • The preorder traversal of the root‘s left subtree, 
     
   • The preorder traversal of the root‘s right subtree.

The preorder traversal of the tree in Figure 1 is KGCBDHQMPY. 

A tree like the one in Figure 1 is also a binary search tree of letters. A binary search tree of letters is a binary tree of letters in which each node satisfies: 

The root‘s data comes later in the alphabet than all the data in the nodes in the left subtree. 

The root‘s data comes earlier in the alphabet than all the data in the nodes in the right subtree. 

The problem: 

Consider the following sequence of operations on a binary search tree of letters 

Remove the leaves and list the data removed 
Repeat this procedure until the tree is empty 
Starting from the tree below on the left, we produce the sequence of trees shown, and then the empty tree 

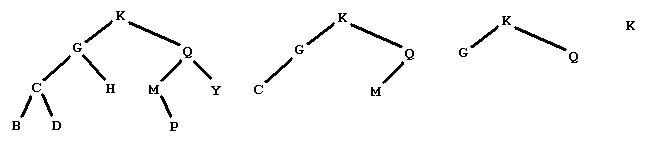
by removing the leaves with data 

BDHPY 
CM 
GQ 
K 

Your problem is to start with such a sequence of lines of leaves from a binary search tree of letters and output the preorder traversal of the tree.

The input will contain one or more data sets. Each data set is a sequence of one or more lines of capital letters. 

The lines contain the leaves removed from a binary search tree in the stages described above. The letters on a line will be listed in increasing alphabetical order. Data sets are separated by a line containing only an asterisk (‘*‘). 

The last data set is followed by a line containing only a dollar sign (‘$‘). There are no blanks or empty lines in the input.

For each input data set, there is a unique binary search tree that would produce the sequence of leaves. The output is a line containing only the preorder traversal of that tree, with no blanks.

BDHPY
CM
GQ
K
*
AC
B
$

KGCBDHQMPY
BAC

Mid-Central USA 2000

#include <stdio.h>
#include <string>
#include <algorithm>
#include <vector>
#include <iostream>
using namespace std;

const int MAX_N = 27;

struct Node
{
	char c;
	Node *l, *r;
	Node(char ch='a', Node *lt=NULL, Node *rt=NULL):c(ch), l(lt), r(rt) {}
};
Node pool[MAX_N];
int poolId;

Node *insertTree(Node *rt, char val)
{
	if (!rt)
	{
		pool[poolId].c = val;
		pool[poolId].l = NULL;
		pool[poolId].r = NULL;
		return &pool[poolId++];
	}
	if (val < rt->c) rt->l = insertTree(rt->l, val);
	else rt->r = insertTree(rt->r, val);
	return rt;
}

void preOrderPrint(Node *rt)
{
	if (rt)
	{
		putchar(rt->c);
		preOrderPrint(rt->l);
		preOrderPrint(rt->r);
	}
}

int main()
{
	vector<string> vstr;
	string str;
	while ("$" != str)
	{
		vstr.clear();
		while ((cin>>str) && "*" != str && "$" != str)
		{
			vstr.push_back(str);
		}
		Node *root = NULL;
		poolId = 0;
		for (int i = (int)vstr.size()-1; i >= 0; i--)
		{
			for (int j = 0; j < (int)vstr[i].size(); j++)
			{
				root = insertTree(root, vstr[i][j]); 
			}
		}
		preOrderPrint(root);
		putchar('\n');
	}
	return 0;
}