标签:style blog http io ar color os sp on
http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1413
题意:题中给了图,所以不看字大概也知道
求的是第n个图形的面积。
就是找规律 递推 一类的...
先给结论:
很鬼畜的公式: 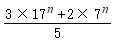
递推式是: 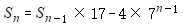
重点在于17和7是怎么来的。
在题图的基础上画些个框框
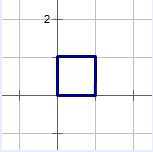
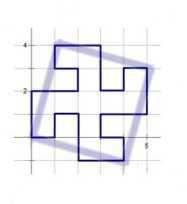
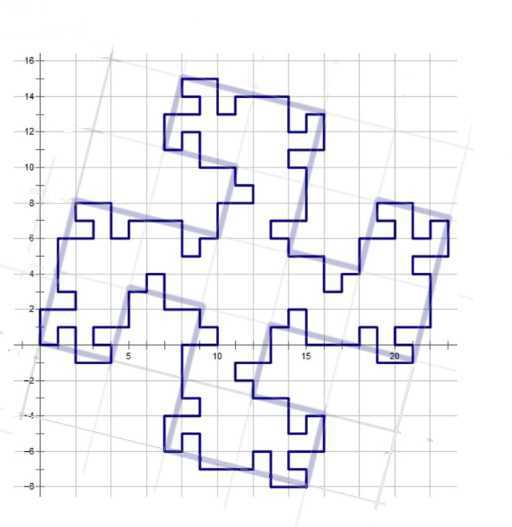
观察可以发现 图1中的 1*1的方格变成了图2中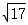 *
*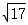 的方格
的方格
其中17就是4*4+1*1
所以第二个方格的面积为前一个方格的17倍。
显然17倍了之后还不是该图形的面积,因为有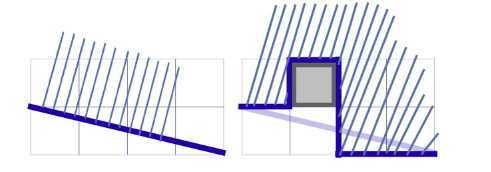 (灰格子)的面积少了。
(灰格子)的面积少了。
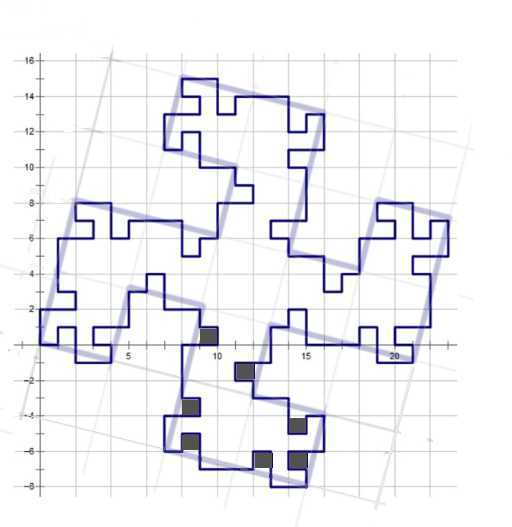
数一下就会发现4个拐中的每个拐都缺了7块
就这样 神奇的7和17都得到了。。。
然后解啊解啊就能解出那个鬼畜的公式了。
有了公式这题就很简单了
只需要用ex_gcd求出5的逆元,然后套一套公式,模一模就完成了~
代码:

1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <climits> 5 #include <cctype> 6 #include <cmath> 7 #include <string> 8 #include <sstream> 9 #include <iostream> 10 #include <algorithm> 11 #include <iomanip> 12 using namespace std; 13 #include <queue> 14 #include <stack> 15 #include <vector> 16 #include <deque> 17 #include <set> 18 #include <map> 19 typedef long long LL; 20 typedef long double LD; 21 const double pi=acos(-1.0); 22 const double eps=1e-6; 23 #define INF 0x3f3f3f 24 #define lson l, m, rt<<1 25 #define rson m+1, r, rt<<1|1 26 typedef pair<int, int> PI; 27 typedef pair<int, PI > PP; 28 #ifdef _WIN32 29 #define LLD "%I64d" 30 #else 31 #define LLD "%lld" 32 #endif 33 //#pragma comment(linker, "/STACK:1024000000,1024000000") 34 //LL quick(LL a, LL b){LL ans=1;while(b){if(b & 1)ans*=a;a=a*a;b>>=1;}return ans;} 35 //inline int read(){char ch=‘ ‘;int ans=0;while(ch<‘0‘ || ch>‘9‘)ch=getchar();while(ch<=‘9‘ && ch>=‘0‘){ans=ans*10+ch-‘0‘;ch=getchar();}return ans;} 36 inline void print(LL x){printf(LLD, x);puts("");} 37 //inline void read(LL &ret){char c;int sgn;LL bit=0.1;if(c=getchar(),c==EOF) return ;while(c!=‘-‘&&c!=‘.‘&&(c<‘0‘||c>‘9‘)) c=getchar();sgn=(c==‘-‘)?-1:1;ret=(c==‘-‘)?0:(c-‘0‘);while(c=getchar(),c>=‘0‘&&c<=‘9‘) ret=ret*10+(c-‘0‘);if(c==‘ ‘||c==‘\n‘){ ret*=sgn; return ; }while(c=getchar(),c>=‘0‘&&c<=‘9‘) ret+=(c-‘0‘)*bit,bit/=10;ret*=sgn;} 38 const int mod=1000000007; 39 40 LL quick(LL a, LL b) 41 { 42 LL ans=1; 43 while(b) 44 { 45 if(b & 1)ans=(ans*a)%mod; 46 a=(a*a)%mod; 47 b>>=1; 48 } 49 return ans%mod; 50 } 51 52 void ex_gcd(int a, int b, int &x, int &y) 53 { 54 if(b) 55 { 56 ex_gcd(b, a%b, x, y); 57 int tmp=x; 58 x=y; 59 y=tmp-(a/b)*y; 60 } 61 else 62 { 63 x=1, y=0; 64 return ; 65 } 66 } 67 int main() 68 { 69 int t; 70 scanf("%d", &t); 71 while(t--) 72 { 73 int n; 74 scanf("%d", &n); 75 if(n==0) 76 { 77 printf("1\n"); 78 continue; 79 } 80 int x, y; 81 ex_gcd(5, mod, x, y); 82 print((((3*quick(17, n))%mod+(2*quick(7, n))%mod)*x)%mod); 83 } 84 return 0; 85 }
[杂题]CSUOJ1413 Area of a Fractal
标签:style blog http io ar color os sp on
原文地址:http://www.cnblogs.com/Empress/p/4152143.html