子图同构

标签：style   blog   http   ar   sp   for   strong   on   2014   

子图同构定义：

      给定图$Q=(V(Q),E(Q),L_V,F)$和$G=(V(G),E(G),L_V‘,F‘)$,  称$Q$子图同构于$G$ 当且仅当存在一个映射$g:V(Q)\rightarrow V(G)$ 使得 

\[\forall x\in V(Q), F(v)=F‘(g(v))\]

和

\[
\forall v_1 ,v_2 \in V(Q),\overrightarrow {v_1 v_2 } \in E(Q) \Rightarrow \overrightarrow {g(v_1 )g(v_2 )} \in E(G)
\]

     例，左图子图同构与右图：

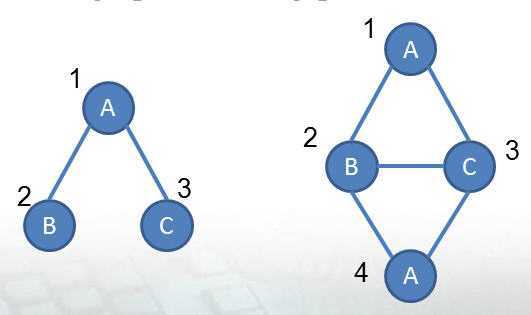
左图  Q                       右图  G

图 1

因为存在映射g（有两种），如下图所示：

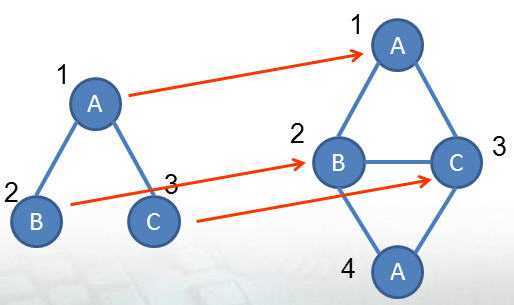
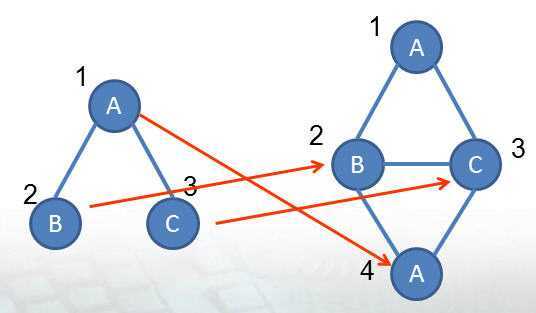
左图  Q                            右图  G                                     左图  Q                           右图  G

图 2                                                                                   图 3

      用$MA,MB$分别表示图$Q,F$的对应的边矩阵，其中$MA[i][j]=1$表示顶点$v_i$与$v_j$有边，$MA[i][j]=0$表示无边. $M‘$表示映射g从$Q$到$G$的映射矩阵，$M‘[i][j]=1$表示$Q$中第$i$个顶点$v_i$对应到$G$中的第$j$个顶点$v_j^‘$，否则没有对应.

      例如，图2中的$Q,G,g$对应的矩阵可以表示为

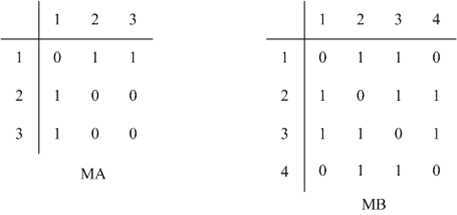
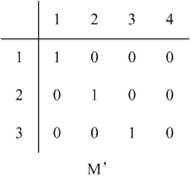
      定理  如果图$Q$关于映射$g$子图同构于$G$，令

\[
MC = M‘(M‘ \cdot MB)^T
\].

，则

\[
\forall i\forall j:(MA[i][j] = 1) \Rightarrow (MC[i][j] = 1).
\]

子图同构

标签：style   blog   http   ar   sp   for   strong   on   2014   

原文地址：http://www.cnblogs.com/huadongw/p/4154295.html