标签：blog http io ar os sp on 数据 div
（1）前言
（2）最小二乘的推导
（3）最小二乘求解线性
（4）曲线拟合的应用
------------------qq：1327706646
-------------------------author：midu
--------------------------------datetime：2014-12-10 17：48：00
（1）前言
关于最小二乘的应用，最早在高斯时代就被天才高斯用来求解，偏离轨道的行星，在别人还在用望远镜寻找的时候，高斯又是神奇般的轻而易举的算出了偏离轨道的行星准确位置。现在学习它，我是想在图像分类中和数据处理分类中会用到他做拟合、预测。
（2）最小二乘的推导
最小二乘的线性回归方程系数即极值点坐标可以用两种方法来求解，结果都是一样的，在大数据处理中的最小二乘的两个系数用贝塔0和贝塔一表示，即方程的b和a，加入回归方程是y=a+bx 在数学推导中。这两种方法是一种相对复杂的配方法最小值代入求解，另一种是关于系数a、lamb的求导求解。这里不管哪种方法，前提都要有两个前提条件equation，推导出来。数据挖据中称之为残差，数学中为方差，如图figure1
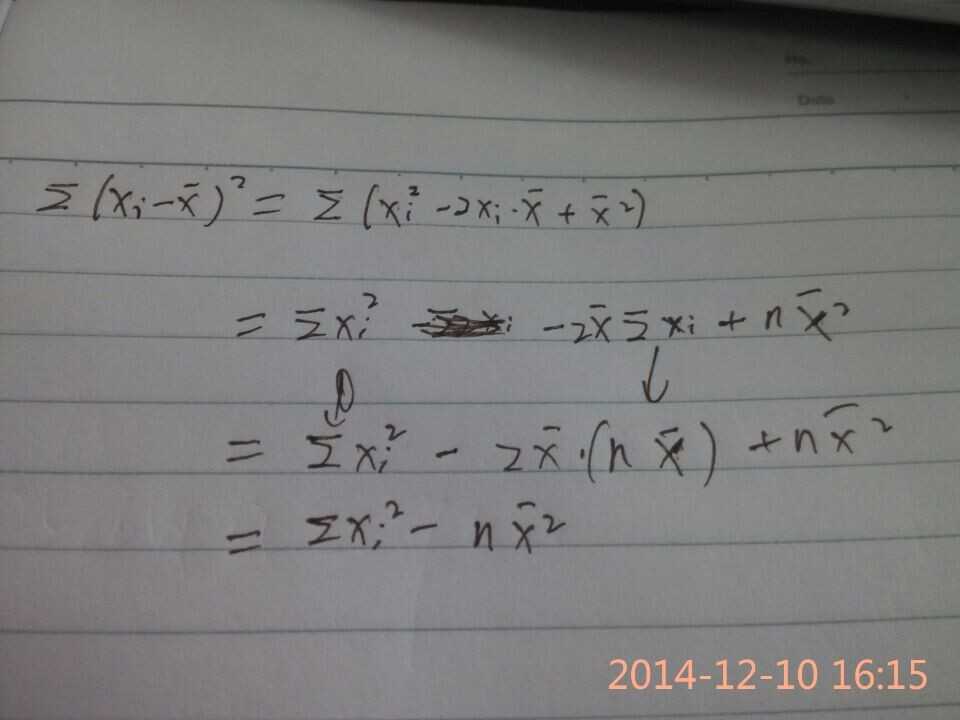
这是其中的公式一：
Σ（xi-x）^2 = Σxi^2 -nx^2;
还有一个公式二：
Σ（xi-x）（yi-y） = Σxiyi - nxy;
然后带入得：
上面利用相关系数为0求得的结果。
下面还有求导同样可以得出推导结果的方法：
普通最小二乘法（ Ordinary Least Square，OLS）：所选择的回归模型应该使所有观察值的残差平方和达到最小。（Q为残差平方和）- 即采用平方损失函数。
样本回归模型：
其中ei为样本（Xi, Yi）的误差
平方损失函数：
则通过Q最小确定这条直线，即确定
，以
为变量，把它们看作是Q的函数，就变成了一个求极值的问题，可以通过求导数得到。求Q对两个待估参数的偏导数：
根据数学知识我们知道，函数的极值点为偏导为0的点。
解得：
这就是最小二乘法的求导解法，就是求得平方损失函数的极值点。
其实除了上面两种方法，还有一中方法可以解释最小二乘，那就是线性代数，如果线数比较差的话，建议推荐看看网易的公开课，里面有个很和蔼的麻省理工老师讲的一节课叫《矩阵投影和最小二乘》，解析的非常清楚，这里应用马云在今年上海浙商商会演讲的一句话“中国的教育，只做了教，育丢弃了”，从这位老师的讲学可以看得出，细心的人会。
（3）最小二乘求解线性
某产品广告支出x万元，与销售额y万元之间有如下数据x=2,4,5,6,8y=30,40,60,50,70(1)求回归直线方程（2）估计广告费为x万元时，销售y收入的值求完整计算谢
(回归方程的公式)
解：(1)设回归线性方程为：y=bx+a
x的平均值=（2+4+5+6+8）/5=5
y的平均值=（30+40+60+50+70）/5=50
∑xi^2=2^2+4^2+5^2+6^2+8^2=145
∑xiyi=2*30+4*40+5*60+6*50+8*70=1380
根据公式：b=（1380-5*5*50）/(145-5*5^2)=6.5
a=50-6.5*5=17.5
则回归线性直线方程为：y=6.5x+17.5
（4）曲线拟合的应用
在线性回归中的应用：
http://baike.baidu.com/link?url=AHp30Rl0sWJZ9EhgknesZ595G0fLCR-KM20aRBLgf6kaqnF7MiixcRQrf7Uu8aKoRqkj8mE2nyZ9Y0wed_UXza
http://baike.baidu.com/view/139822.htm#ref_[1]_139822
参考文献：
http://zh.wikipedia.org/zh-cn/最小二乘法 在学术方面wiki做的相当的好，这里从各个方面讲到了二乘的来龙去脉，包括线数，至于百度百科，我只能呵呵。
http://www.baike.com/wiki/偏最小二乘法
http://wenku.baidu.com/view/61a4260cba1aa8114431d974.html 回归直线方程的推导
http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html 最小二乘的c++代码实现和求导
http://blog.sciencenet.cn/blog-430956-621997.html 最小二乘法，为啥差的不是绝对值
http://wenku.baidu.com/view/81ed83ea998fcc22bcd10dca.html?from=rec&pos=3&weight=2 最小二乘及其残差图
http://blog.csdn.net/viewcode/article/details/8794401 各种回归概念
http://zhidao.baidu.com/link?url=Pl0g2cvqNIuqn-z34JZ7t7Kl9tPMeudfFGy4-GSITWOj8FKhsk3d0M1wFDj_mj6umFcglxGaNlIlL_mPJkF5MK 线性求解
http://blog.csdn.net/wenrenhua08/article/details/2909255 最小三乘法
http://baike.so.com/doc/4551178.html 曲线拟合 matlab 实现 包括多阶
标签：blog http io ar os sp on 数据 div
原文地址：http://www.cnblogs.com/pengkunfan/p/4156266.html
