标签:des blog http io ar os sp for on
 % KALMANF - updates a system state vector estimate based upon an
% KALMANF - updates a system state vector estimate based upon an % observation, using a discrete Kalman filter.
% observation, using a discrete Kalman filter. %
% % Version 1.0, June 30, 2004
% Version 1.0, June 30, 2004 %
% % This tutorial function was written by Michael C. Kleder
% This tutorial function was written by Michael C. Kleder % (Comments are appreciated at: public@kleder.com)
% (Comments are appreciated at: public@kleder.com) %
% % INTRODUCTION
% INTRODUCTION %
% % Many people have heard of Kalman filtering, but regard the topic
% Many people have heard of Kalman filtering, but regard the topic % as mysterious. While it‘s true that deriving the Kalman filter and
% as mysterious. While it‘s true that deriving the Kalman filter and % proving mathematically that it is "optimal" under a variety of
% proving mathematically that it is "optimal" under a variety of % circumstances can be rather intense, applying the filter to
% circumstances can be rather intense, applying the filter to % a basic linear system is actually very easy. This Matlab file is
% a basic linear system is actually very easy. This Matlab file is % intended to demonstrate that.
% intended to demonstrate that. %
% % An excellent paper on Kalman filtering at the introductory level,
% An excellent paper on Kalman filtering at the introductory level, % without detailing the mathematical underpinnings, is:
% without detailing the mathematical underpinnings, is: % "An Introduction to the Kalman Filter"
% "An Introduction to the Kalman Filter" % Greg Welch and Gary Bishop, University of North Carolina
% Greg Welch and Gary Bishop, University of North Carolina % http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html
% http://www.cs.unc.edu/~welch/kalman/kalmanIntro.html %
% % PURPOSE:
% PURPOSE: %
% % The purpose of each iteration of a Kalman filter is to update
% The purpose of each iteration of a Kalman filter is to update % the estimate of the state vector of a system (and the covariance
% the estimate of the state vector of a system (and the covariance % of that vector) based upon the information in a new observation.
% of that vector) based upon the information in a new observation. % The version of the Kalman filter in this function assumes that
% The version of the Kalman filter in this function assumes that % observations occur at fixed discrete time intervals. Also, this
% observations occur at fixed discrete time intervals. Also, this % function assumes a linear system, meaning that the time evolution
% function assumes a linear system, meaning that the time evolution % of the state vector can be calculated by means of a state transition
% of the state vector can be calculated by means of a state transition % matrix.
% matrix. %
% % USAGE:
% USAGE: %
% % s = kalmanf(s)
% s = kalmanf(s) %
% % "s" is a "system" struct containing various fields used as input
% "s" is a "system" struct containing various fields used as input % and output. The state estimate "x" and its covariance "P" are
% and output. The state estimate "x" and its covariance "P" are % updated by the function. The other fields describe the mechanics
% updated by the function. The other fields describe the mechanics % of the system and are left unchanged. A calling routine may change
% of the system and are left unchanged. A calling routine may change % these other fields as needed if state dynamics are time-dependent;
% these other fields as needed if state dynamics are time-dependent; % otherwise, they should be left alone after initial values are set.
% otherwise, they should be left alone after initial values are set. % The exceptions are the observation vectro "z" and the input control
% The exceptions are the observation vectro "z" and the input control % (or forcing function) "u." If there is an input function, then
% (or forcing function) "u." If there is an input function, then % "u" should be set to some nonzero value by the calling routine.
% "u" should be set to some nonzero value by the calling routine. %
% % SYSTEM DYNAMICS:
% SYSTEM DYNAMICS: %
% % The system evolves according to the following difference equations,
% The system evolves according to the following difference equations, % where quantities are further defined below:
% where quantities are further defined below: %
% % x = Ax + Bu + w meaning the state vector x evolves during one time
% x = Ax + Bu + w meaning the state vector x evolves during one time % step by premultiplying by the "state transition
% step by premultiplying by the "state transition % matrix" A. There is optionally (if nonzero) an input
% matrix" A. There is optionally (if nonzero) an input % vector u which affects the state linearly, and this
% vector u which affects the state linearly, and this % linear effect on the state is represented by
% linear effect on the state is represented by % premultiplying by the "input matrix" B. There is also
% premultiplying by the "input matrix" B. There is also % gaussian process noise w.
% gaussian process noise w. % z = Hx + v meaning the observation vector z is a linear function
% z = Hx + v meaning the observation vector z is a linear function % of the state vector, and this linear relationship is
% of the state vector, and this linear relationship is % represented by premultiplication by "observation
% represented by premultiplication by "observation % matrix" H. There is also gaussian measurement
% matrix" H. There is also gaussian measurement % noise v.
% noise v. % where w ~ N(0,Q) meaning w is gaussian noise with covariance Q
% where w ~ N(0,Q) meaning w is gaussian noise with covariance Q % v ~ N(0,R) meaning v is gaussian noise with covariance R
% v ~ N(0,R) meaning v is gaussian noise with covariance R %
% % VECTOR VARIABLES:
% VECTOR VARIABLES: %
% % s.x = state vector estimate. In the input struct, this is the
% s.x = state vector estimate. In the input struct, this is the % "a priori" state estimate (prior to the addition of the
% "a priori" state estimate (prior to the addition of the % information from the new observation). In the output struct,
% information from the new observation). In the output struct, % this is the "a posteriori" state estimate (after the new
% this is the "a posteriori" state estimate (after the new % measurement information is included).
% measurement information is included). % s.z = observation vector
% s.z = observation vector % s.u = input control vector, optional (defaults to zero).
% s.u = input control vector, optional (defaults to zero). %
% % MATRIX VARIABLES:
% MATRIX VARIABLES: %
% % s.A = state transition matrix (defaults to identity).
% s.A = state transition matrix (defaults to identity). % s.P = covariance of the state vector estimate. In the input struct,
% s.P = covariance of the state vector estimate. In the input struct, % this is "a priori," and in the output it is "a posteriori."
% this is "a priori," and in the output it is "a posteriori." % (required unless autoinitializing as described below).
% (required unless autoinitializing as described below). % s.B = input matrix, optional (defaults to zero).
% s.B = input matrix, optional (defaults to zero). % s.Q = process noise covariance (defaults to zero).
% s.Q = process noise covariance (defaults to zero). % s.R = measurement noise covariance (required).
% s.R = measurement noise covariance (required). % s.H = observation matrix (defaults to identity).
% s.H = observation matrix (defaults to identity). %
% % NORMAL OPERATION:
% NORMAL OPERATION: %
% % (1) define all state definition fields: A,B,H,Q,R
% (1) define all state definition fields: A,B,H,Q,R % (2) define intial state estimate: x,P
% (2) define intial state estimate: x,P % (3) obtain observation and control vectors: z,u
% (3) obtain observation and control vectors: z,u % (4) call the filter to obtain updated state estimate: x,P
% (4) call the filter to obtain updated state estimate: x,P % (5) return to step (3) and repeat
% (5) return to step (3) and repeat %
% % INITIALIZATION:
% INITIALIZATION: %
% % If an initial state estimate is unavailable, it can be obtained
% If an initial state estimate is unavailable, it can be obtained % from the first observation as follows, provided that there are the
% from the first observation as follows, provided that there are the % same number of observable variables as state variables. This "auto-
% same number of observable variables as state variables. This "auto- % intitialization" is done automatically if s.x is absent or NaN.
% intitialization" is done automatically if s.x is absent or NaN. %
% %x = inv(H)*z
%x = inv(H)*z %P = inv(H)*R*inv(H‘)
%P = inv(H)*R*inv(H‘) %
% % This is mathematically equivalent to setting the initial state estimate
% This is mathematically equivalent to setting the initial state estimate % covariance to infinity.
% covariance to infinity. %
% % SCALAR EXAMPLE (Automobile Voltimeter):
% SCALAR EXAMPLE (Automobile Voltimeter): %
% % % Define the system as a constant of 12 volts:
% % Define the system as a constant of 12 volts: function T
function T clear s
clear s s.x = 12;
s.x = 12; s.A = 1;
s.A = 1; % % Define a process noise (stdev) of 2 volts as the car operates:
% % Define a process noise (stdev) of 2 volts as the car operates: s.Q = 2^2; % variance, hence stdev^2
s.Q = 2^2; % variance, hence stdev^2 % Define the voltimeter to measure the voltage itself:
% Define the voltimeter to measure the voltage itself: s.H = 1;
s.H = 1; % % Define a measurement error (stdev) of 2 volts:
% % Define a measurement error (stdev) of 2 volts: s.R = 2^2; % variance, hence stdev^2
s.R = 2^2; % variance, hence stdev^2 %Do not define any system input (control) functions:
%Do not define any system input (control) functions: s.B = 0;
s.B = 0; s.u = 0;
s.u = 0; % % Do not specify an initial state:
% % Do not specify an initial state: s.x = nan;
s.x = nan; s.P = nan;
s.P = nan; % % Generate random voltages and watch the filter operate.
% % Generate random voltages and watch the filter operate. tru=[]; % truth voltage
tru=[]; % truth voltage for t=1:20
for t=1:20 tru(end+1) = randn*2+12;
tru(end+1) = randn*2+12; s(end).z = tru(end) + randn*2; % create a measurement
s(end).z = tru(end) + randn*2; % create a measurement s(end+1)=kalmanf(s(end)); % perform a Kalman filter iteration
s(end+1)=kalmanf(s(end)); % perform a Kalman filter iteration % end
% end % figure
% figure % hold on
% hold on % grid on
% grid on % % plot measurement data:
% % plot measurement data: hz=plot([s(1:end-1).z],‘r‘);hold on
hz=plot([s(1:end-1).z],‘r‘);hold on % % plot a-posteriori state estimates:
% % plot a-posteriori state estimates: hk=plot([s(2:end).x],‘b-‘);hold on
hk=plot([s(2:end).x],‘b-‘);hold on ht=plot(tru,‘g-‘);hold on
ht=plot(tru,‘g-‘);hold on legend(‘observations‘,‘Kalman output‘,‘true voltage‘,0)
legend(‘observations‘,‘Kalman output‘,‘true voltage‘,0) title(‘Automobile Voltimeter Example‘)
title(‘Automobile Voltimeter Example‘) % hold off
% hold off end
end 
 function s = kalmanf(s)
function s = kalmanf(s)
 % set defaults for absent fields:
% set defaults for absent fields: if ~isfield(s,‘x‘); s.x=nan*z; end
if ~isfield(s,‘x‘); s.x=nan*z; end if ~isfield(s,‘P‘); s.P=nan; end
if ~isfield(s,‘P‘); s.P=nan; end if ~isfield(s,‘z‘); error(‘Observation vector missing‘); end
if ~isfield(s,‘z‘); error(‘Observation vector missing‘); end if ~isfield(s,‘u‘); s.u=0; end
if ~isfield(s,‘u‘); s.u=0; end if ~isfield(s,‘A‘); s.A=eye(length(x)); end
if ~isfield(s,‘A‘); s.A=eye(length(x)); end if ~isfield(s,‘B‘); s.B=0; end
if ~isfield(s,‘B‘); s.B=0; end if ~isfield(s,‘Q‘); s.Q=zeros(length(x)); end
if ~isfield(s,‘Q‘); s.Q=zeros(length(x)); end if ~isfield(s,‘R‘); error(‘Observation covariance missing‘); end
if ~isfield(s,‘R‘); error(‘Observation covariance missing‘); end if ~isfield(s,‘H‘); s.H=eye(length(x)); end
if ~isfield(s,‘H‘); s.H=eye(length(x)); end
 if isnan(s.x)
if isnan(s.x) % initialize state estimate from first observation
% initialize state estimate from first observation if diff(size(s.H))
if diff(size(s.H)) error(‘Observation matrix must be square and invertible for state autointialization.‘);
error(‘Observation matrix must be square and invertible for state autointialization.‘); end
end s.x = inv(s.H)*s.z;
s.x = inv(s.H)*s.z; s.P = inv(s.H)*s.R*inv(s.H‘);
s.P = inv(s.H)*s.R*inv(s.H‘);  else
else
 % This is the code which implements the discrete Kalman filter:
% This is the code which implements the discrete Kalman filter:
 % Prediction for state vector and covariance:
% Prediction for state vector and covariance: s.x = s.A*s.x + s.B*s.u;
s.x = s.A*s.x + s.B*s.u; s.P = s.A * s.P * s.A‘ + s.Q;
s.P = s.A * s.P * s.A‘ + s.Q;
 % Compute Kalman gain factor:
% Compute Kalman gain factor: K = s.P*s.H‘*inv(s.H*s.P*s.H‘+s.R);
K = s.P*s.H‘*inv(s.H*s.P*s.H‘+s.R);
 % Correction based on observation:
% Correction based on observation: s.x = s.x + K*(s.z-s.H*s.x);
s.x = s.x + K*(s.z-s.H*s.x); s.P = s.P - K*s.H*s.P;
s.P = s.P - K*s.H*s.P;
 % Note that the desired result, which is an improved estimate
% Note that the desired result, which is an improved estimate % of the sytem state vector x and its covariance P, was obtained
% of the sytem state vector x and its covariance P, was obtained % in only five lines of code, once the system was defined. (That‘s
% in only five lines of code, once the system was defined. (That‘s % how simple the discrete Kalman filter is to use.) Later,
% how simple the discrete Kalman filter is to use.) Later, % we‘ll discuss how to deal with nonlinear systems.
% we‘ll discuss how to deal with nonlinear systems.
 end
end

 % 状态
% 状态 % xk=A•xk-1+B•uk+wk
% xk=A•xk-1+B•uk+wk % zk=H•xk+vk,
% zk=H•xk+vk, % p(w) ~ N(0,Q)
% p(w) ~ N(0,Q) % p(v) ~ N(0,R),
% p(v) ~ N(0,R),
 % 预测
% 预测 % x‘k=A•xk+B•uk
% x‘k=A•xk+B•uk % P‘k=A•P(k-1)*AT + Q
% P‘k=A•P(k-1)*AT + Q % 修正
% 修正 % Kk=P‘k•HT•(H•P‘k•HT+R)-1
% Kk=P‘k•HT•(H•P‘k•HT+R)-1 % xk=x‘k+Kk•(zk-H•x‘k)
% xk=x‘k+Kk•(zk-H•x‘k) % Pk=(I-Kk•H)•P‘k
% Pk=(I-Kk•H)•P‘k
 %要注意的是:必须把系统状态和kalman滤波器内部预测的状态分开
%要注意的是:必须把系统状态和kalman滤波器内部预测的状态分开 function Test
function Test A=[1 0.1;0 1];
A=[1 0.1;0 1]; B=0;
B=0; Xp=rand(2,1)*0.1;
Xp=rand(2,1)*0.1;  X=[0 0]‘;
X=[0 0]‘; H=[1 0];
H=[1 0]; Q=eye(2)*1e-5;
Q=eye(2)*1e-5; R=eye(1)*0.1;
R=eye(1)*0.1;  P=eye(2);% P‘(k)
P=eye(2);% P‘(k) angle=[];
angle=[]; angle_m=[];
angle_m=[]; angle_real=[];
angle_real=[]; for i=1:500
for i=1:500 angle_real=[angle_real X(1)]; %实际角度
angle_real=[angle_real X(1)]; %实际角度
 [Xp,P]=Predict(A,Xp,P,Q);
[Xp,P]=Predict(A,Xp,P,Q); 
 X=A*X+rand(2,1)*1e-5;
X=A*X+rand(2,1)*1e-5; z_m=H*X+rand(1,1)*0.1-0.05;
z_m=H*X+rand(1,1)*0.1-0.05;  angle_m=[angle_m z_m(1)]; %测量的角度
angle_m=[angle_m z_m(1)]; %测量的角度
 [Xp,P]=Correct(P,H,R,X,z_m);
[Xp,P]=Correct(P,H,R,X,z_m); angle=[angle Xp(1)]; %预测的角度
angle=[angle Xp(1)]; %预测的角度  end
end t=1:500;
t=1:500; plot(t,angle,‘r‘,t,angle_m,‘g‘,t,angle_real,‘b‘)
plot(t,angle,‘r‘,t,angle_m,‘g‘,t,angle_real,‘b‘) legend(‘预测值‘,‘测量值‘,‘实际值‘)
legend(‘预测值‘,‘测量值‘,‘实际值‘)
 figure
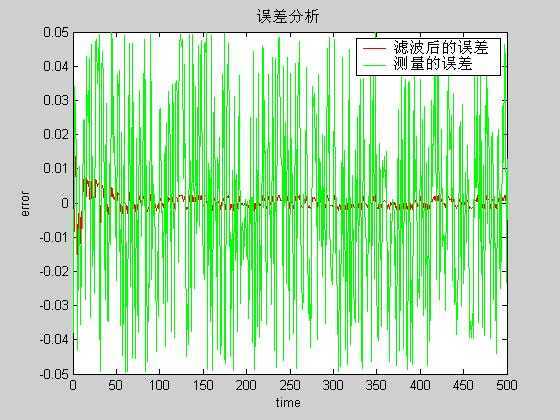
figure plot(t,angle-angle_real,‘r‘,t,angle_m-angle_real,‘g‘)
plot(t,angle-angle_real,‘r‘,t,angle_m-angle_real,‘g‘) legend(‘滤波后的误差‘,‘测量的误差‘)
legend(‘滤波后的误差‘,‘测量的误差‘) title(‘误差分析‘)
title(‘误差分析‘) xlabel(‘time‘);
xlabel(‘time‘); ylabel(‘error‘);
ylabel(‘error‘);
 function [Xk,Pk]=Predict(A,Xk,Pk_1,Q)
function [Xk,Pk]=Predict(A,Xk,Pk_1,Q) Xk=A*Xk;
Xk=A*Xk; Pk=A*Pk_1*A‘+Q;
Pk=A*Pk_1*A‘+Q;
 function [Xk,Pk]=Correct(Pk,H,R,Xk,zk)
function [Xk,Pk]=Correct(Pk,H,R,Xk,zk) Kk=Pk * H‘ * inv(H * Pk * H‘ + R);
Kk=Pk * H‘ * inv(H * Pk * H‘ + R); Xk=Xk+ Kk*(zk-H*Xk);
Xk=Xk+ Kk*(zk-H*Xk); Pk=(eye(size(Pk,1)) - Kk*H)*Pk;
Pk=(eye(size(Pk,1)) - Kk*H)*Pk;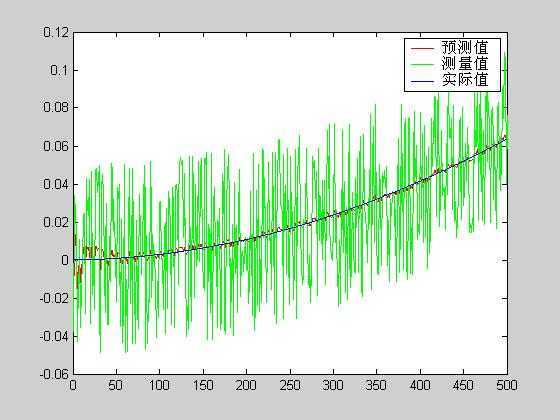
标签:des blog http io ar os sp for on
原文地址:http://www.cnblogs.com/x113/p/4160734.html