标签:style blog class c code java
//====================================================
决策树的构造:
构造决策树时,需要解决的第一个问题是,当前数据集上那个特征在划分数据是起决定性作用。为了找到决定性特征,我们必须使用某种度量来评估每个特征。完成评估之后,找到决定性特征,使用该特征划分数据,原始的数据集就被划分为几个数据子集。这个子集会发布在第一个决策点的所有分支。如果某个分支下的数据属于同一类型,则当前已经准确划分数据分类。如果数据子集内的数据不属于同一类型,则需要重复划分数据子集的过程。划分数据的方法跟划分原始数据的方法相同。
本文使用ID3算法划分数据集,每次划分时只取一个特征属性,如果数据集有多个特征,如何选取决定性特征?在采用量化的方法判断如何划分数据。
//====================================================
信息增益:
划分数据集的最大原则是:将无序的数据变得更加有序。一种方法是使用信息论度量信息。
在划分数据集之前之后信息发生的变化称为信息增益。可以计算每个特征值划分数据集获得的信息增益,获得的信息增益最高的特征就是最好的选择。
计算信息增益:
集合信息的度量方式称为香农熵或者熵,定义为信息的期望值。
信息(xi)的定义:如果待分类的事务可能划分在多个分类之中,则符号xi的信息定义为l(xi)=-log2 p(xi),其中p(xi)是选择该分类的概率
计算熵,计算所有分类所有可能值包含的信息期望值:H=-Σp(xi)*log2 p(xi)
python计算熵的代码如下:
def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts = {} for featVec in dataSet: currentLabel = featVec[-1] if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0; for key in labelCounts: prob = float(labelCounts[key]) / numEntries shannonEnt -= prob * log(prob, 2) return shannonEnt
//=====================================================
划分数据集代码:
def splitDataSet(dataSet, axis, value): retDataSet = [] for featVec in dataSet: if featVec[axis] == value: reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSet
dataSet为待划分的数据集
axis为划分数据的特征
value为划分数据的特征的值
结果为返回划分好数据的特征
选择最好的数据集划分方式:
def chooseBestFeatureToSplit(dataSet): numFeatures = len(dataSet[0]) - 1 baseEntroy = calcShannonEnt(dataSet) bestInfoGain = 0.0 bestFeature = -1 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy = 0.0 for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet) / float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) infoGain = baseEntroy - newEntropy if infoGain > bestInfoGain: bestInfoGain = infoGain bestFeature = i return bestFeature
dataSet每行的最后一个元素为该行特征的标签
//===============================================
构造决策树,原理:得倒原始数据,基于最好的属性值划分数据集,由于特征值可能对于两个,因此可能存在大于两个分支的数据划分。第一次划分之后,在数据将被向下传递到树分支的下一个节点,在这个节点上我们再次划分数据。因此可以采用递归的方法划分数据。
递归的结束条件:程序遍历完所有的特征或者每个分支下所有的数据都属于同一分类。但是递归结束后,某个节点的数据不一定都属于同一分类。此时我们需决定该节点的分类。这种情况下我们通常采用多票表决的方法。
代码如下:
def majorityCnt(classList): classCounts = {} for vote in classList: if vote not in classCounts.keys(): classCounts[vote] = 0 classCounts[vote] += 1 sortedClassCount = sorted(classCounts.iteritems(), key = operator.itemgetter(1), reverse = True) return sortedClassCount
构造决策树的代码:
def createTree(dataSet, labels): classList = [example[-1] for example in dataSet] if classList.count(classList[0]) == len(classList): return classList[0] if len(dataSet[0]) == 1: return majorityCnt(classList) bestFeat = chooseBestFeatureToSplit(dataSet) bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel:{}} del(labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) return myTree
//=============================================
构造完决策树,我们就可以使用决策树执行分类。
分类的代码如下:
def classify(inputTree, featLabels, testVec): firstStr = inputTree.keys()[0] secondDict = inputTree[firstStr] featIndex = featLabels.index(firstStr) for key in secondDict.keys(): if testVec[featIndex] == key: if type(secondDict[key]).__name__ == ‘dict‘: classLabel = classify(secondDict[key], featLabels, testVec) else: classLabel = secondDict[key] return classLabel
//==============================================
使用python中的Matplotlib库绘制决策树树形图。
代码如下:
#-*- encoding: utf-8 -*- ‘‘‘ Created on 2014??5??19?? @author: jsy ‘‘‘ import matplotlib.pyplot as plt import trees decisionNode = dict(boxstyle = ‘sawtooth‘, fc = ‘0.8‘) leafNode = dict(boxstyle = ‘round4‘, fc = ‘0.8‘) arrow_args = dict(arrowstyle = ‘<-‘) def plotNode(nodeTxt, centerPt, parentPt, nodeType): createPlot.ax1.annotate(nodeTxt, xy = parentPt, xycoords = ‘axes fraction‘, xytext = centerPt, ha = ‘center‘, bbox = nodeType, arrowprops = arrow_args) # def createPlot(): # fig = plt.figure(1, facecolor = ‘white‘) # fig.clf() # createPlot.ax1 = plt.subplot(111, frameon = False) # plotNode(‘a decision node‘, (0.5, 0.1), (0.1, 0.5), decisionNode) # plotNode(‘a leaf node‘, (0.8, 0.1), (0.3, 0.8), leafNode) # plt.show() def getNumLeafs(myTree): numLeafs = 0 firstStr = myTree.keys()[0] sencondDict = myTree[firstStr] for key in sencondDict.keys(): if type(sencondDict[key]).__name__ == ‘dict‘: numLeafs += getNumLeafs(sencondDict[key]) else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): maxDepth = 0 firstStr = myTree.keys()[0] sencondDict = myTree[firstStr] for key in sencondDict.keys(): if type(sencondDict[key]).__name__ == ‘dict‘: thisDepth = 1 + getTreeDepth(sencondDict[key]) else: thisDepth = 1 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def retrieveTree(i): listOfTrees = [{‘no surfacing‘ : { 0 : ‘no‘, 1 : {‘flippers‘ : {0 : ‘no‘, 1 : ‘yes‘}}}}, {‘no surfacing‘ : {0 : ‘no‘, 1 : {‘flippers‘ : {0 : {‘head‘ : {0 : ‘no‘, 1 : ‘yes‘}}, 1 : ‘no‘}}}}] return listOfTrees[i] def plotMidText(cntPt, parentPt, txtString): xMid = (parentPt[0] - cntPt[0]) / 2.0 + cntPt[0] yMid = (parentPt[1] - cntPt[1]) / 2.0 + cntPt[1] createPlot.ax1.text(xMid, yMid, txtString) def plotTree(myTree, parentPt, nodeTxt): numLeafs = getNumLeafs(myTree) depth = getTreeDepth(myTree) firstStr = myTree.keys()[0] cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff) plotMidText(cntrPt, parentPt, nodeTxt) plotNode(firstStr, cntrPt, parentPt, decisionNode) sencondDict = myTree[firstStr] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in sencondDict.keys(): if type(sencondDict[key]).__name__ == ‘dict‘: plotTree(sencondDict[key], cntrPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW plotNode(sencondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD def createPlot(inTree): fig = plt.figure(1, facecolor = ‘white‘) fig.clf() axprops = dict(xticks = [], yticks = []) createPlot.ax1 = plt.subplot(111, frameon = False, **axprops) plotTree.totalW = float(getNumLeafs(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = -0.5 / plotTree.totalW plotTree.yOff = 1.0 plotTree(inTree, (0.5, 1.0), ‘‘) plt.show() if __name__ == ‘__main__‘: # createPlot() # print retrieveTree(1) # myTree = retrieveTree(0) # print getNumLeafs(myTree) # print getTreeDepth(myTree) dataSet, labels = trees.createDataSet() inTree = trees.createTree(dataSet, labels) inTree = retrieveTree(1) createPlot(inTree)
绘制的效果如下:
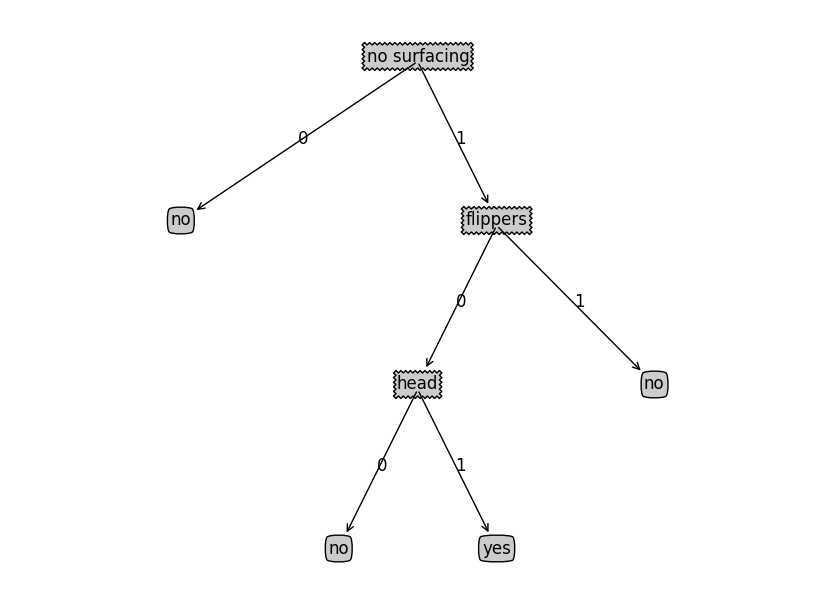
//====================================
总的代码:http://pan.baidu.com/s/1bnla1HH
机器学习实战-决策树(ID3),布布扣,bubuko.com
标签:style blog class c code java
原文地址:http://www.cnblogs.com/zjwzcnjsy/p/3740255.html