算法导论读书笔记(13)
目录
红黑树
红黑树 是一种二叉查找树,但在每个结点上增加了一个存储位表示结点的颜色,可以是 RED 或
BLACK
。通过对任何一条从根到叶子的路径上的各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍,因而是接近平衡的。红黑树(red-black
tree)是许多“平衡的”查找树中的一种,它能保证在最坏情况下,基本的动态集合操作的时间为 O ( lg n )。
树中每个结点包含五个域: color , key , left , right 和
p 。如果某结点没有一个子结点或父结点,则该结点相应的指针为 NIL 。我们将这些 NIL
视为指向二叉查找树外结点(叶子)的指针,而把带关键字的结点视为树的内结点。
一棵红黑树需要满足下面的 红黑性质 :
- 每个结点或是红的,或是黑的。
- 根结点是黑的。
- 每个叶结点(
NIL)是黑的。 - 如果一个结点是红的,则它的两个孩子都是黑的。
- 对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
下图给出了一棵红黑树的例子。
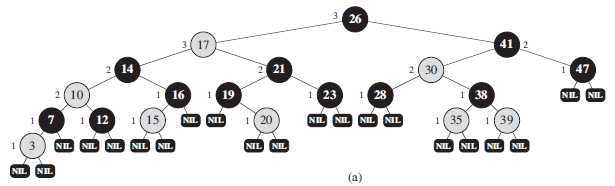
为了便于处理红黑树代码中的边界条件,我们采用一个哨兵来代表 NIL 。对一棵红黑树来说,哨兵 T.nil
是一个与树内普通结点有相同域的对象。它的 color 域为 BLACK
,而其他域可以设为任意允许的值。如下图所示,所有指向 NIL 的指针都被替换成指向哨兵 T.nil 的指针。
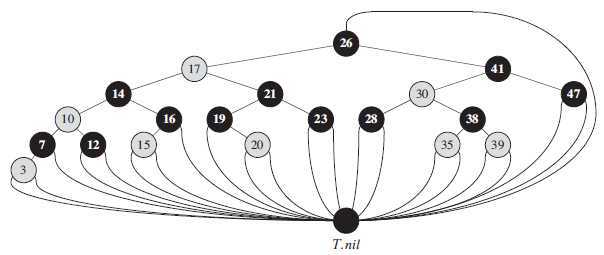
使用哨兵后,可以将结点 x 的 NIL 孩子视为一个其父结点为 x
的普通结点。这里我们用一个哨兵 T.nil 来代表所有的 NIL (所有的叶子以及根部的父结点)。
通常我们将注意力放在红黑树的内部结点上,因为它们存储了关键字的值。因此本文其余部分都将忽略红黑树的叶子,如下图所示。
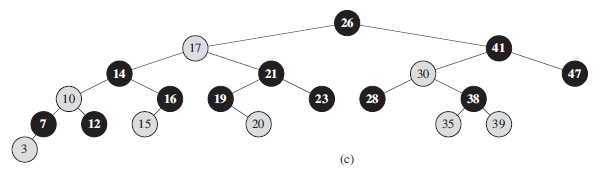
从某个结点 x 出发(不包括该结点)到达一个叶结点的任意一条路径上,黑色结点的个数称为该结点 x 的 黑高度 ,用bh( x )表示。红黑树的黑高度定义为其根结点的黑高度。
引理
一棵有 n 个内结点的红黑树的高度至多为2lg(
n + 1 )。
旋转
当在含 n 个关键字的红黑树上运行时,查找树操作 TREE-INSERT 和
TREE-DELETE 的时间为 O ( lg n
)。由于这两个操作对树做了修改,结果可能违反了红黑树的性质,为保持红黑树的性质,就要改变树中某些结点的颜色和指针结构。
指针结构的修改是通过 旋转 来完成的,这是一种能保持二叉查找树性质的查找树局部操作。下图给出了两种旋转:左旋和右旋。

当在某个结点 x 上做左旋时,我们假设它的右孩子 y 不是 T.nil ; x 可以为树内任意右孩子不是 T.nil 的结点。左旋以 x 到 y 之间的链为“支轴”进行。它使 y 称为该子树新的根, x 成为 y 的左孩子,而 y 的左孩子则成为 x 的右孩子。
在 LEFT-ROTATE 的伪码中,假设 x.right != T.nil
,并且根的父结点是 T.nil 。
LEFT-ROTATE(T, x) 1 y = x.right // set y 2 x.right = y.left // turn y‘s left subtree into s‘s right subtree 3 if y.left != T.nil 4 y.left.p = x 5 y.p = x.p 6 if x.p == T.nil 7 T.root = y 8 elseif x == x.p.left 9 x.p.left = y 10 else 11 x.p.right = y 12 y.left = x // put x on y‘s left 13 x.p = y
下图显示了 LEFT-ROTATE 的操作过程。 RIGHT-ROTATE 的程序是对称的。它们都在
O ( 1 )时间内完成。
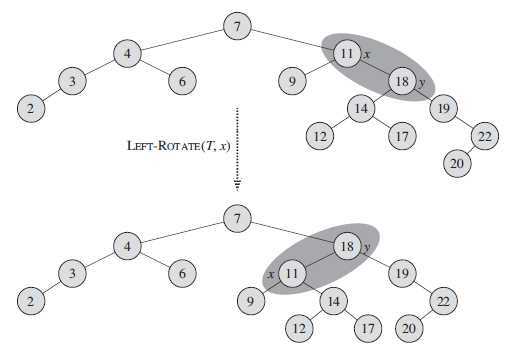
RIGHT-ROTATE(T, x) 1 y = x.left 2 x.left = y.right 3 if y.right != T.nil 4 y.right.p = x 5 y.p = x.p 6 if x.p == T.nil 7 T.root = y 8 elseif x == x.p.left 9 x.p.left = y 10 else 11 x.p.right = right 12 y.right = x 13 x.p = y
插入
向一棵含 n 个结点的红黑树 T 中插入一个新结点 z 的操作可在 O ( lg
n )时间内完成。首先将结点 z 插入树 T 中,就好像 T
是一棵普通的二叉查找树一样,然后将 z 着为红色。为保证红黑性质,这里要调用一个辅助程序
RB-INSERT-FIXUP 来对结点重新着色并旋转。调用 RB-INSERT 会将 z
插入红黑树 T 内,假设 z 的 key 域已经事先被赋值。
RB-INSERT(T, z) 1 y = T.nil 2 x = T.root 3 while x != T.nil 4 y = x 5 if z.key < x.key 6 x = x.left 7 else 8 x = x.right 9 z.p = y 10 if y == T.nil 11 T.root = z 12 elseif z.key < y.key 13 y.left = z 14 else 15 y.right = z 16 z.left = T.nil 17 z.right = T.nil 18 z.color = RED 19 RB-INSERT-FIXUP(T, z)
过程 RB-INSERT 的运行时间为 O ( lg n )。过程 TREE-INSERT
和 RB-INSERT 之间有四处不同。首先,在 TREE-INSERT 内的所有的
NIL 都被 T.nil 代替。其次,在 RB-INSERT 的第16,17行中,设置
z.left 和 z.right 为 T.nil ,来保持正确的树结构。第三,在第18行将
z 着为红色。第四,在最后一行,调用 RB-INSERT-FIXUP 来保持红黑性质。
RB-INSERT-FIXUP(T, z) 1 while z.p.color == RED 2 if z.p == z.p.p.left // z的父结点是其父结点的左孩子 3 y = z.p.p.right // 令y为z的叔父结点 4 if y.color == RED 5 z.p.color = BLACK // case 1 6 y.color = BLACK // case 1 7 z.p.p.color = RED // case 1 8 z = z.p.p // case 1 9 else 10 if z == z.p.right 11 z = z.p // case 2 12 LEFT-ROTATE(T, z) // case 2 13 z.p.color = BLACK // case 3 14 z.p.p.color = RED // case 3 15 RIGHT-ROTATE(T, z.p.p) // case 3 16 else // z的父结点是其父结点的右孩子 17 y = z.p.p.left // 令y为z的叔父结点 18 if y.color = RED 19 z.p.color = BLACK 20 y.color = BLACK 21 z.p.p.color = RED 22 z = z.p.p 23 else 24 if z = z.p.left 25 z = z.p 26 RIGHT-ROTATE(T, z) 27 z.p.color = BLACK 28 z.p.p.color = RED 29 LEFT-ROTATE(T, z.p.p) 30 T.root.color = BLACK
下图显示了在一棵红黑树上 RB-INSERT-FIXUP 是如何操作的。
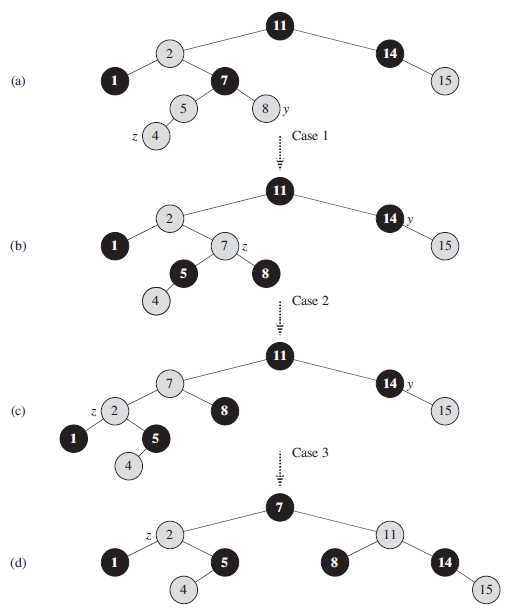
要理解 RB-INSERT-FIXUP 的工作过程,需要分三个主要步骤来分析其代码。首先,确定当结点 z
被插入并着色为红色后,红黑性质有哪些不能保持。其次,分析 while 循环的总目标。最后,具体分析
while 循环中的三种情况。
在调用 RB-INSERT-FIXUP 时,红黑性质中的性质1和性质3会继续成立,因为新插入结点的子女都是哨兵
T.nil 。性质5也会成立,因为结点 z 代替了(黑色)哨兵,且结点 z
本身是具有哨兵子女的红色结点。因此,可能被破坏的就是性质2和性质4。这是因为 z 被着为红色,如果 z
是根结点则破坏了性质2,如果 z 的父结点是红色则破坏了性质4。上图a显示在结点 z 被插入后性质4被破坏。
要保持树的红黑性质,实际上一共要考虑六种情况,但其中三种与另外三种是对称的,区别在于 z 的父结点 z.p 是 z 的祖父结点 z.p.p 的左孩子还是右孩子。这里只讨论 z.p 是左孩子的情况。
上面伪码中情况1和情况2,3的区别在于 z 的叔父结点的颜色有所不同。如果 y 是红色,则执行情况1。否则,控制转移到情况2和情况3上。在所有三种情况中, z 的祖父 z.p.p 都是黑色的,因为它的父结点 z.p 是红色的,故性质4只在 z 和 z.p 之间被破坏了。
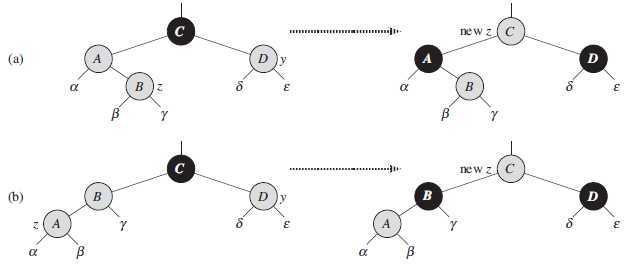
情况1 : z 的叔父结点 y 是红色的
下图显示的是情况1(第5~8行)的状况。只有在 z.p 和 y 都是红色的时候才执行。既然
z.p.p 是黑色的,我们可以将 z.p 和 y 都着为黑色以解决 z 和
z.p 都是红色的问题,将 z.p.p 着为红色以保持性质5。然后把 z.p.p 当作新增的结点
z 来重复 while 循环。指针 z 在树中上移两层。
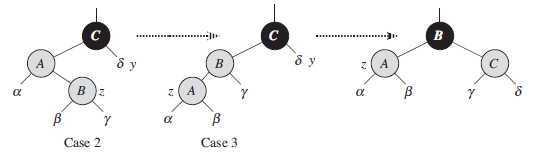
情况2 : z 的叔父结点 y 是黑色的,而且 z 是右孩子
情况3 : z 的叔父结点 y 是黑色的,而且 z 是左孩子
在情况2和情况3中, z 的叔父结点 y 是黑色的。这两种情况通过 z 是 z.p 的左孩子还是右孩子来区别。在情况2中,结点 z 是其父结点的右孩子。我们立刻使用一个左旋来将此状况转变为情况3,此时结点 z 成为左孩子。因为 z 和 z.p 都是红色的,所以所做的旋转对结点的黑高度和性质5都无影响。至此, z 的叔父结点 y 总是黑色的,另外 z.p.p 存在且其身份保持不变。在情况3中,要改变某些结点的颜色,并作一次右旋以保持性质5。这样,由于在一行中不再有两个连续的红色结点,所有的处理到此结束。
删除
和 n 个结点的红黑树上的其它基本操作一样,对一个结点的删除要花 O ( lg n )时间。
首先,我们需要自定义一个类似于 TREE-DELETE 中调用的 TRANSPLANT
的子程序。该过程接收三个参数,红黑树 T 以及两棵子树 u , v 。过程用子树 v
来替代子树 u 在树中的位置。
RB-TRANSPLANT(T, u, v) 1 if u.p == T.nil 2 T.root = v 3 elseif u == u.p.left 4 u.p.left = v 5 else 6 u.p.right = v 7 v.p = u.p
过程 RB-TRANSPLANT 和 TRANSPLANT 有两点不同。首先,第1行使用哨兵
T.nil 替代 NIL 。其次,第7行的赋值语句不再需要条件。
过程 RB-DELETE 同 TREE-DELETE
类似,但是多了些代码。有些代码用于跟踪记录可能破坏红黑性质的结点 y 的状态。如果待删除的结点 z
的孩子结点少于两个,那么可以直接从树中删除 z ,并让 y 等于 z 。如果待删除的结点
z 有两个孩子,令 y 为 z 的后继,并用 y 替代 z
在树中的位置。我们还要记住 y 在删除或移动之前的颜色。由于结点 x
也可能破坏树的红黑性质,我们也需要跟踪记录下这个占据了结点 y 最初位置的结点 x 的状态。删除结点 z
后,过程 RB-DELETE 还要调用 RB-DELETE-FIXUP 以保持红黑性质。
RB-DELETE(T, z) 1 y = z 2 y-original-color = y.color 3 if z.left == T.nil 4 x = z.right 5 RB-TRANSPLANT(T, z, z.right) 6 elseif z.right == T.nil 7 x = z.left 8 RB-TRANSPLANT(T, z, z.left) 9 else 10 y = TREE-MINIMUM(z.right) 11 y-original-color = y.color 12 x = y.right 13 if y.p == z 14 x.p = y 15 else 16 RB-TRANSPLANT(T, y, y.right) 17 y.right = z.right 18 y.right.p = y 19 RB-TRANSPLANT(T, z, y) 20 y.left = z.left 21 y.left.p = y 22 y.color = z.color 23 if y-original-color == BLACK 24 RB-DELETE-FIXUP(T, x)
RB-DELETE 和 TREE-DELETE 主要的不同之处罗列如下:
- 我们维护了一个结点 y 。第1行令 y 指向了结点 z (此时 z 为待删结点且它的孩子结点少于两个)。当 z 有两个孩子结点时,第10行令 y 指向 z 的后继,然后 y 会取代 z 在树中的位置。
- 由于 y 的颜色可能发生变化,变量 y-original-color 保存了 y
在发生改变之前的颜色。在为 y 赋值后,第2行和第10行立刻设置了该变量。如果 z 有两个孩子结点,那么
y != z 并且 y 会占据结点 z 在红黑树中的初始位置;第22行将
y 的颜色设置成和 z 一样。我们需要保存 y 的初始颜色以便在过程
RB-DELETE结尾处做测试;如果它是黑色的,那么删除或移动结点 y 就会破坏红黑性质。 - 我们还要跟踪记录结点 x 的状态。第4,7和12行的赋值语句令 x 指向 y 的孩子结点或哨兵 T.nil 。
- 一旦结点 x 移入 y 的初始位置,属性 x.p 总是指向 y
的父结点,哪怕 x 是哨兵 T.nil 也一样。除非 z 是 y 的父结点(此时
z 有两个孩子且 y 是它的右孩子)。对 x.p 的赋值操作在过程
RB-TRANSPLANT中第7行执行(通过观察可以看出来,在第5,8和16行被调用的RB-TRANSPLANT,其传递的第二个参数就是 x )。 - 最后,如果结点 y 是黑色的,我们可能会破坏某些红黑性质,这就需要调用
RB-DELETE-FIXUP来保持红黑性质。
在 RB-DELETE 中,如果被删除的结点 y 是黑色的,则会产生三个问题。首先,如果 y
原来是根结点,而 y 的某个红色孩子成为了新的根,这就违反了性质2。其次,如果 x 和 x.p
都是红色的,就违反了性质4。第三,删除 y 可能导致其路径上黑结点的个数少1,这就违反了性质5。补救的一个办法就是把结点 x
视为还有额外一重黑色。即,如果将任意包含结点 x 的路径上黑结点个数加1,则性质5成立。当将黑结点 y
删除时,将其黑色“下推”至其子结点。这样问题变为结点 x 可能既不是红色,也不是黑色,从而违反了性质1。这时需要调用
RB-DELETE-FIXUP 来纠正。
RB-DELETE-FIXUP(T, x) 1 while x != T.root and x.color == BLACK 2 if x == x.p.left 3 w = x.p.right 4 if w.color == RED 5 w.color = BLACK // case 1 6 x.p.color = RED // case 1 7 LEFT-ROTATE(T, x.p) // case 1 8 w = x.p.right // case 1 9 if w.left.color == BLACK and w.right.color == BLACK 10 w.color = RED // case 2 11 x = x.p // case 2 12 else 13 if w.right.color == BLACK 14 w.left.color = BLACK // case 3 15 w.color = RED // case 3 16 RIGHT-ROTATE(T, w) // case 3 17 w = x.p.right // case 3 18 w.color = x.p.color // case 4 19 x.p.color = BLACK // case 4 20 w.right.color = BLACK // case 4 21 LEFT-ROTATE(T, x.p) // case 4 22 x = T.root // case 4 23 else (same as then clause with "right" and "left" exchanged) 24 x.color = BLACK
过程 RB-DELETE-FIXUP 可以恢复性质1,2和4。这里仅说明性质1。过程中 while
循环的目标是将额外的黑色沿树上移,直到:
- x 指向一个红黑结点,此时,在第24行,将 x 着为黑色;
- x 指向根,这是可以简单地消除额外的黑色,或者
- 做必要的旋转和颜色改变。
在 while 循环中, x 总是指向具有双重黑色的那个非根结点。用 w 表示
x
的兄弟。算法中的四种情况在下图中加以说明。首先要说明的是在每种情况中的变换是如何保持性质5的。关键思想就在每种情况下,从(其包括)子树的根到每棵子树之间的黑结点个数(包括
x 的额外黑色)并不被变换所改变。因此,性质5在变换之前成立,之后依然成立。
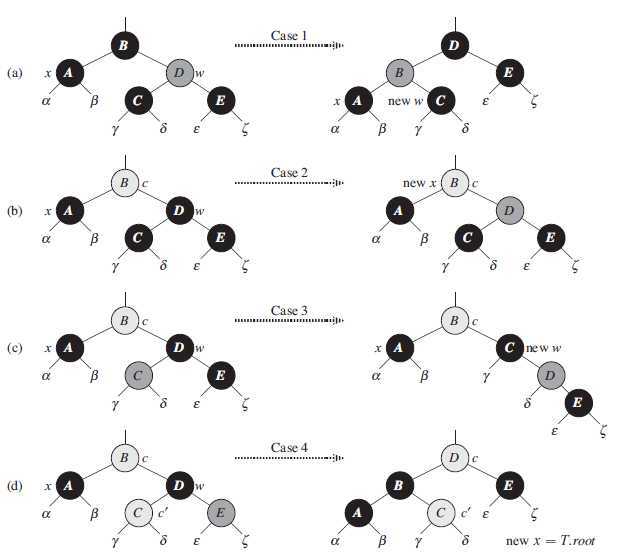
情况1 : x 的兄弟 w 是红色的
见 RB-DELETE-FIXUP 第5~8行和上图a。因为 w 必须有红色孩子,我们可以改变
w 和 x.p 的颜色,再对 x.p 做一次左旋,而且红黑性质得以继续保持, x
的新兄弟是旋转之前 w 的某个孩子,其颜色为黑色。这样,情况1就转换成情况2,3或4。
情况2 : x 的兄弟 w 是黑色的,且 w 的两个孩子都是黑色的
见 RB-DELETE-FIXUP 第10~11行和上图b。因为 w 和两个孩子都是黑色的,故从
x 和 w 上各去掉一重黑色,从而 x 只有一重黑色而 w
为红色。为了补偿去掉的黑色,需要在原 x.p 内新增一重额外黑色。然后新结点 x 在最后被着为黑色。
情况3 : x 的兄弟 w 是黑色的, w 的左孩子是红色的,右孩子是黑色的
见 RB-DELETE-FIXUP 第14~17行和上图c。此时可以交换 w 和其左孩子
w.left 的颜色,并对 w 右旋,而红黑性质依然保持,且从情况3转换成了情况1。
情况4 : x 的兄弟 w 是黑色的,且 w 的右孩子是红色的
见 RB-DELETE-FIXUP 第18~22行和上图d。通过做颜色的修改并对 x.p 做一次左旋,可以去掉
x 的额外黑色并把它变成单独黑色。将 x 置为根后, while
会在测试其循环条件时结束。
