#include<cmath>
#include<iostream.h>
#include<fstream.h>
int main()
{
double NJZ(double
sum[100][100],double l[10]);
double
x[10],y[10],X[10],Y[10],Z[10],d,D,m,f,T,R,S,r=0,s=0,t=0;
ifstream
infile; //定义输入文件类
infile.open("测试_1.txt"); //打开一个输入文件“file1.txt”
for(int
i=1;i<=4;i++)
{
for(int
j=1;j<=5;j++)
{
switch(j)
{
case
1:infile>>x[i];break;
case
2:infile>>y[i];break;
case
3:infile>>X[i];break;
case
4:infile>>Y[i];break;
case
5:infile>>Z[i];break;
}
//infile>>a[i][j];//将“file1.txt”中的十个整型数输入到a[i]中
}
}
//for(i=1;i<=4;i++)
//{
//cout<<x[i]<<","<<y[i]<<","<<X[i]<<","<<Y[i]<<","<<Z[i]<<endl;
//}
//cout<<endl;
infile.close();//关闭输入文件
d=sqrt(pow(x[1]-x[2],2)+pow(y[1]-y[2],2));
//cout<<"d="<<d<<endl;
D=sqrt(pow(X[1]-X[2],2)+pow(Y[1]-Y[2],2)+pow(Z[1]-Z[2],2));
//cout<<"D="<<D<<endl;
m=D/d;
//cout<<"m="<<m<<endl;
//cout<<"请输入像片主距f(以mm为单位):";
//cin>>f;
f=153.24;
T=m*f;
//cout<<"T="<<T<<endl;
R=0.25*(X[1]+X[2]+X[3]+X[4]);
//cout<<"R="<<R<<endl;
S=0.25*(Y[1]+Y[2]+Y[3]+Y[4]);
//cout<<"S="<<S<<endl;
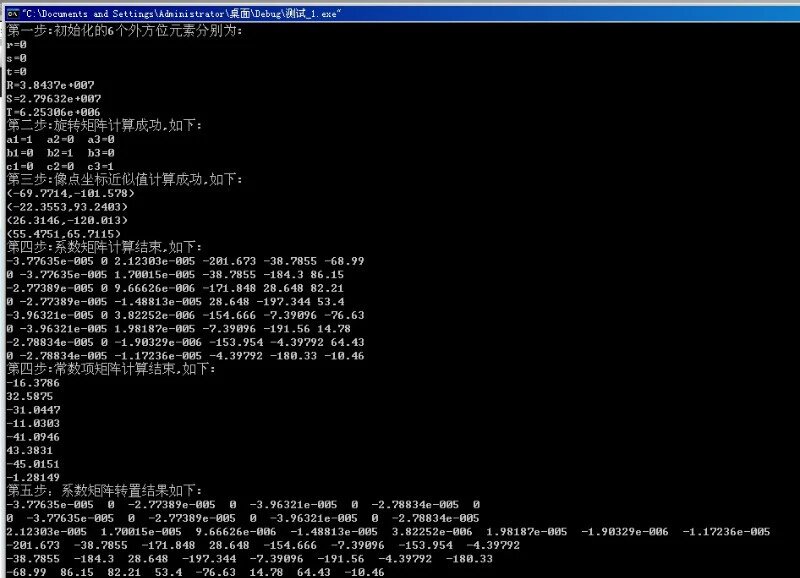
cout<<"第一步:初始化的6个外方位元素分别为:"<<endl;
cout<<"r=0"<<endl;
cout<<"s=0"<<endl;
cout<<"t=0"<<endl;
cout<<"R="<<R<<endl;
cout<<"S="<<S<<endl;
cout<<"T="<<T<<endl;
double
a1,a2,a3,b1,b2,b3,c1,c2,c3;
a1=cos(r)*cos(t)-sin(r)*sin(s)*sin(t);
a2=-cos(r)*sin(t)-sin(r)*sin(s)*cos(t);
a3=-sin(r)*cos(s);
b1=cos(s)*sin(t);
b2=cos(s)*cos(t);
b3=-sin(s);
c1=sin(r)*cos(t)+cos(r)*sin(s)*sin(t);
c2=-sin(r)*sin(t)+cos(r)*sin(s)*cos(t);
c3=cos(r)*cos(s);
cout<<"第二步:旋转矩阵计算成功,如下:"<<endl;
cout<<"a1="<<a1<<"
"<<"a2="<<a2<<"
"<<"a3="<<a3<<endl;
cout<<"b1="<<b1<<"
"<<"b2="<<b2<<"
"<<"b3="<<b3<<endl;
cout<<"c1="<<c1<<"
"<<"c2="<<c2<<"
"<<"c3="<<c3<<endl;
//逐点计算像点坐标的近似值
double
u[5],v[5],U[5],V[5],W[5];
for(i=1;i<=4;i++)
{
U[i]=a1*(X[i]-R)+b1*(Y[i]-S)+c1*(Z[i]-T);
V[i]=a2*(X[i]-R)+b2*(Y[i]-S)+c2*(Z[i]-T);
W[i]=a3*(X[i]-R)+b3*(Y[i]-S)+c3*(Z[i]-T);
u[i]=-f*U[i]/W[i];
v[i]=-f*V[i]/W[i];
}
cout<<"第三步:像点坐标近似值计算成功,如下:"<<endl;
for(i=1;i<=4;i++)
{
cout<<"("<<u[i]<<","<<v[i]<<")"<<endl;
}
//计算系数矩阵
double
a[10][10];
for(i=1;i<=4;i++)
{
a[2*i-1][1]=(a1*f+a3*x[i])/W[i];
a[2*i-1][2]=(b1*f+b3*x[i])/W[i];
a[2*i-1][3]=(c1*f+c3*x[i])/W[i];
a[2*i-1][4]=y[i]*sin(s)-cos(s)*(x[i]*(x[i]*cos(t)-y[i]*sin(t))/f+f*cos(t));
a[2*i-1][5]=-f*sin(t)-x[i]*(x[i]*sin(t)+y[i]*cos(t))/f;
a[2*i-1][6]=y[i];
a[2*i][1]=(a2*f+a3*y[i])/W[i];
a[2*i][2]=(b2*f+b3*y[i])/W[i];
a[2*i][3]=(c2*f+c3*y[i])/W[i];
a[2*i][4]=-x[i]*sin(s)-cos(s)*(y[i]*(x[i]*cos(t)-y[i]*sin(t))/f-f*sin(t));
a[2*i][5]=-f*cos(t)-y[i]*(x[i]*sin(t)+y[i]*cos(t))/f;
a[2*i][6]=-x[i];
}
cout<<"第四步:系数矩阵计算结束,如下:"<<endl;
for(i=1;i<=4;i++)
{
cout<<a[2*i-1][1]<<"
"<<a[2*i-1][2]<<" "<<a[2*i-1][3]<<"
"<<a[2*i-1][4]<<" "<<a[2*i-1][5]<<"
"<<a[2*i-1][6]<<endl;
cout<<a[2*i][1]<<" "<<a[2*i][2]<<"
"<<a[2*i][3]<<" "<<a[2*i][4]<<"
"<<a[2*i][5]<<"
"<<a[2*i][6]<<endl;
}
//计算常数项
double
l[10];
for(i=1;i<=8;i++)
{
l[2*i-1]=x[i]-u[i];
l[2*i]=y[i]-v[i];
}
cout<<"第四步:常数项矩阵计算结束,如下:"<<endl;
for(i=1;i<=8;i++)
{
cout<<l[i]<<endl;
}
//求系数矩阵的转置
int
q=0;
double
sum[100][100],A[100][100];
for(i=1;i<=8;i++)
{
for(int
j=1;j<=6;j++)
{
A[j][i]=a[i][j];
}
}
cout<<"第五步:系数矩阵转置结果如下:"<<endl;
for(i=1;i<=6;i++)
{
for(int
j=1;j<=8;j++)
{
cout<<A[i][j]<<"
";
}
cout<<endl;
}
//求系数矩阵与其转置矩阵的乘积
for(i=1;i<=6;i++)
{
for(int
k=1;k<=6;k++)
{
sum[i][k]=0;
for(int
j=1;j<=8;j++)
{
sum[i][k]=sum[i][k]+A[i][j]*a[j][k];
}
}
}
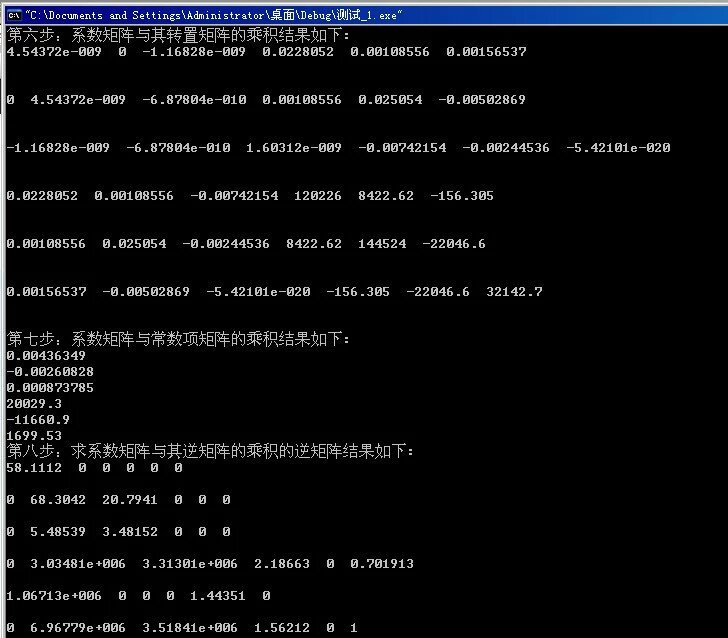
cout<<"第六步:系数矩阵与其转置矩阵的乘积结果如下:"<<endl;
for(i=1;i<=6;i++)
{
for(int
j=1;j<=6;j++)
{
cout<<sum[i][j]<<"
";
}
cout<<endl<<endl<<endl;
}
//求系数矩阵与常数项矩阵的乘积
double
mun[10];
for(i=1;i<=6;i++)
{
mun[i]=0;
for(int
j=1;j<=8;j++)
{
mun[i]=mun[i]+A[i][j]*l[j];
}
}
cout<<"第七步:系数矩阵与常数项矩阵的乘积结果如下:"<<endl;
for(i=1;i<=6;i++)
{
cout<<mun[i]<<endl;
}
NJZ(sum,l);
return 0;
}
double NJZ(double sum[100][100],double
l[10])
{
int i,j,n=6,q,k,c=0;
double
A[100],C[100][100],B[100][100],G[100][100],K[10];
for(i=1;i<=n;i++)
{
for(j=n+1;j<=2*n;j++)
{
//判断
if(i==j-n)
{
sum[i][j]=1;
}
else
{
sum[i][j]=0;
}
}
}
// cout<<"第一步:为原矩阵配单位矩阵结果如下:"<<endl;
// for(i=1;i<=n;i++)
// {
// for(j=1;j<=2*n;j++)
// {
// cout<<sum[i][j]<<"
";
// }
// cout<<endl;
// }
for(j=1;j<=n;j++)//列
{
for(i=1;i<=n;i++)
{
if(i!=j)
{
if(sum[i][j]!=0)
{
for(k=1;k<=2*n;k++)
{
B[i][k]=sum[i][k]-sum[j][k]*sum[i][j]/sum[j][j];
}
for(k=1;k<=2*n;k++)
{
sum[i][k]=B[i][k];
}
}
}
else
{
if(sum[i][j]==0)//若对角线上的=0
{
for(q=1;q<=n;q++)//从第1行找起,找到不为0的行与其交换
{
if(sum[q][j]!=0)
{
for(k=1;k<=2*n;k++)
{
c++;
A[k]=sum[i][k];
sum[i][k]=sum[q][k];
sum[q][k]=A[k];
}
break;
}
}
}
}
//if(j==3&&i==3)
//{
// cout<<a[1][1]<<"
"<<a[1][2]<<" "<<a[1][3]<<" "<<a[1][4]<<"
"<<a[1][5]<<"
"<<a[1][6]<<endl;
// cout<<a[2][1]<<"
"<<a[2][2]<<" "<<a[2][3]<<" "<<a[2][4]<<"
"<<a[2][5]<<"
"<<a[2][6]<<endl;
// cout<<a[3][1]<<"
"<<a[3][2]<<" "<<a[3][3]<<" "<<a[3][4]<<"
"<<a[3][5]<<"
"<<a[3][6]<<endl;
//}
}
}
for(j=1;j<=n;j++)
{
if(sum[j][j]!=1)
{
for(k=1;k<=2*n;k++)
{
sum[j][k]=sum[j][k]/sum[j][j];
}
}
}
cout<<"第八步:求系数矩阵与其逆矩阵的乘积的逆矩阵结果如下:"<<endl;
for(i=1;i<=n;i++)
{
for(j=1;j<=2*n;j++)
{
if(sum[i][j]<0.00001)
{
sum[i][j]=0;
}
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
G[i][j]=sum[i][j+n];
}
}
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
cout<<G[i][j]<<"
";
}
cout<<endl<<endl;
}
//求解6个外方位元素的改正数
for(i=1;i<=6;i++)
{
K[i]=0;
for(j=1;j<=6;j++)
{
K[i]=K[i]+G[i][j]*l[j];
}
}
cout<<"第九步:6个外方位元素的改正数结果如下:"<<endl;
for(i=1;i<=6;i++)
{
cout<<K[i]<<endl;
}
return 0;
}